Навигация
Оптимальний розподіл інвестицій, як задача динамічного програмування
3. Оптимальний розподіл інвестицій, як задача динамічного програмування
Інвестор виділяє кошти в розмірі ![]() умовних одиниць, котрі повинні бути розподілені між
умовних одиниць, котрі повинні бути розподілені між ![]() -підприємствами. Кожне і-те підприємство при інвестуванні в нього коштів
-підприємствами. Кожне і-те підприємство при інвестуванні в нього коштів ![]() приносить прибуток
приносить прибуток ![]() умовних одиниць,
умовних одиниць, ![]() . Необхідно вибрати оптимальний розподіл інвестицій між підприємствами, котрий забезпечить максимальний прибуток.
. Необхідно вибрати оптимальний розподіл інвестицій між підприємствами, котрий забезпечить максимальний прибуток.
Виграшем ![]() у даній задачі є прибуток, принесена
у даній задачі є прибуток, принесена ![]() підприємствами.
підприємствами.
Побудова математичної моделі.
– Визначення числа кроків. Число кроків ![]() дорівнює числу підприємств, в котрі здійснюється інвестування.
дорівнює числу підприємств, в котрі здійснюється інвестування.
– Визначення станів системи. Стан системи на кожному кроці характеризується кількістю коштів ![]() , наявних перед даним кроком,
, наявних перед даним кроком, ![]() .
.
– Вибір крокових управлінь. Управлінням на і-му кроці ![]() ,
, ![]() є кількість коштів, котрі інвестуються і-те підприємство.
є кількість коштів, котрі інвестуються і-те підприємство.
– Функція виграшу на і-му кроці:
![]() . (3.1)
. (3.1)
– це прибуток, котрий приносить і-те підприємство при інвестуванні в нього коштів ![]() .
.
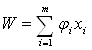 . (3.2)
. (3.2)
Отже, дана задача може бути вирішена методом динамічного програмування.
– Визначення функції переходу в новий стан:
![]() . (3.3)
. (3.3)
Таким чином, якщо на і-му кроці система знаходиться у стані ![]() , а вибрано управління
, а вибрано управління ![]() , то на (і+1)-му кроці система буде знаходитись у стані
, то на (і+1)-му кроці система буде знаходитись у стані ![]() . Іншими словами, якщо в наявності маються кошти в розмірі
. Іншими словами, якщо в наявності маються кошти в розмірі ![]() умовних одиниць, й в і-те підприємство інвестуються
умовних одиниць, й в і-те підприємство інвестуються ![]() умовних одиниць, то для подальшого інвестування залишається
умовних одиниць, то для подальшого інвестування залишається ![]() умовних одиниць.
умовних одиниць.
– Складанні функціонального рівняння для ![]() .
.
![]() . (3.4)
. (3.4)
А також:
![]() . (3.5)
. (3.5)
На останньому кроці, тобто перед інвестування коштів в останнє підприємство, умовне оптимальне управління відповідає кількості коштів, що маються в наявності; тобто скільки коштів залишилось, стільки й необхідно вкласти в останнє підприємство. Умовний оптимальний виграш дорівнює прибутку, котрий приноситься останнім підприємством.
– Складання основного функціонального рівняння.
Підставивши у формулу (2.13) вираження (3.1) і (3.3), отримуємо наступне функціональне рівняння:
![]() . (3.6)
. (3.6)
Пояснюючи дане рівняння зазначається, що нехай перед і-м кроком в інвестора залишились кошти у розмірі ![]() умовних одиниць. Тоді
умовних одиниць. Тоді ![]() умовних одиниць він може вкласти в і-те підприємство, при цьому даний вклад принесе дохід
умовних одиниць він може вкласти в і-те підприємство, при цьому даний вклад принесе дохід ![]() , а
, а ![]() умовних одиниць, що залишились – в останні підприємства з (
умовних одиниць, що залишились – в останні підприємства з (![]() )-го до
)-го до ![]() -го. Умовний оптимальний виграш від такого вкладу
-го. Умовний оптимальний виграш від такого вкладу ![]() . Оптимальним буде те умовне управління
. Оптимальним буде те умовне управління ![]() , при якому сума
, при якому сума ![]() і
і ![]() максимальна.
максимальна.
Проведення автоматизації розподілу інвестицій між підприємствами здійснюється із застосуванням ЕОМ, оснащеної спеціальним програмним засобом MS EXCEL. До розгляду береться, що ![]() =5000,
=5000, ![]() =3.
=3.
Таблиця 3.1 – Прибуток ![]() підприємств
підприємств ![]() , від інвестування в них коштів
, від інвестування в них коштів
|
|
|
|
|
| 1 | 1,5 | 2 | 1,7 |
| 2 | 2 | 2,1 | 2,4 |
| 3 | 2,5 | 2,3 | 2,7 |
| 4 | 3 | 3,5 | 3,2 |
| 5 | 3,6 | 4 | 3,5 |
Для ![]()
![]() ,
, ![]() .
.
Вхідні умови зображені на рисунку А.1 (Додаток А). Для простоти у задачі зроблено припущення, що вкладаються тільки тисячі умовних одиниць. Проводиться умовна оптимізація. По її результатам заповнюється таблиця 3.2.
Таблиця 3.2 – Результати умовної оптимізації
| s |
|
|
| |||
|
|
|
|
|
|
| |
| 1 | 1 | 1,7 | 0 | 2 | ||
| 2 | 2 | 2,4 | 1 | 3,7 | ||
| 3 | 3 | 2,7 | 1 | 4,4 | ||
| 4 | 4 | 3,2 | 1 | 4,7 | ||
| 5 | 5 | 3,5 | 1/4 | 5,2 | 2 | 6,4 |
У першій колонці таблиці записуються можливі стани системи ![]() , у верхньому рядку – номера кроків
, у верхньому рядку – номера кроків ![]() . На кожному кроці визначаються умовні оптимальні управління
. На кожному кроці визначаються умовні оптимальні управління ![]() і умовні оптимальні виграші
і умовні оптимальні виграші ![]() ,
, ![]() ;
; ![]() .
.
Детальний розгляд результатів умовної оптимізації.
а) Проведення умовної оптимізації для останнього кроку ![]() . Функціональне рівняння на останньому кроці має вигляд:
. Функціональне рівняння на останньому кроці має вигляд:
![]() ,
, ![]() . (3.7)
. (3.7)
На рисунку 3.1 ілюстраційно зображено результати проведення умовної оптимізації для останнього кроку.
Виходячи з цього, два стовпця таблиці 3.2, котрі відповідають ![]() , заповнюються автоматично по таблиці вихідних даних.
, заповнюються автоматично по таблиці вихідних даних.
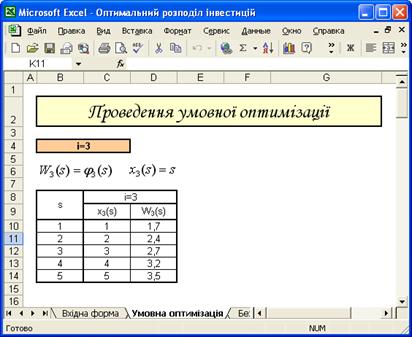
Рисунок 3.1 – Результати умовної оптимізації для останнього кроку
б) Умовна оптимізація для ![]() .
.
Функціональне рівняння має вигляд:
![]() . (3.8)
. (3.8)
Для проведення умовної оптимізації заповнюються допоміжні таблиці 3.3–3.7, котрі відповідають різним значенням ![]() , тобто різним закінченням попереднього кроку, результати практичного дослідження відображені на рисунках А.2–А.4 (Додаток А).
, тобто різним закінченням попереднього кроку, результати практичного дослідження відображені на рисунках А.2–А.4 (Додаток А).
Таблиця 3.3 – Наявність коштів у розмірі ![]() умовних одиниць після закінченням попереднього кроку
умовних одиниць після закінченням попереднього кроку
|
|
|
|
|
|
| 0 | 1 | 0 | 1,7 | 1,7 |
| 1 | 0 | 2 | 0 | 2 |
![]() , звідси:
, звідси:
– ![]() ;
;
– ![]() .
.
Таблиця 3.4 – Наявність коштів у розмірі ![]() умовних одиниць після закінченням попереднього кроку
умовних одиниць після закінченням попереднього кроку
|
|
|
|
|
|
| 0 | 2 | 0 | 2,4 | 2,4 |
| 1 | 1 | 2 | 1,7 | 3,7 |
| 2 | 0 | 2,1 | 0 | 2,1 |
![]() , звідси:
, звідси:
– ![]() ;
;
– ![]() .
.
Таблиця 3.5 – Наявність коштів у розмірі ![]() умовних одиниць після закінченням попереднього кроку
умовних одиниць після закінченням попереднього кроку
|
|
|
|
|
|
| 0 | 3 | 0 | 2,7 | 2,7 |
| 1 | 2 | 2 | 2,4 | 4,4 |
| 2 | 1 | 2,1 | 1,7 | 3,8 |
| 3 | 0 | 2,3 | 0 | 2,3 |
![]() , звідси:
, звідси:
– ![]() ;
;
– ![]() .
.
Таблиця 3.6 – Наявність коштів у розмірі ![]() умовних одиниць після закінченням попереднього кроку
умовних одиниць після закінченням попереднього кроку
|
|
|
|
|
|
| 0 | 4 | 0 | 3,2 | 3,2 |
| 1 | 3 | 2 | 2,7 | 4,7 |
| 2 | 2 | 2,1 | 2,4 | 4,5 |
| 3 | 1 | 2,3 | 1,7 | 4 |
| 4 | 0 | 3,5 | 0 | 3,5 |
![]() , звідси:
, звідси: ![]() ; –
; – ![]() .
.
Таблиця 3.7 – Наявність коштів у розмірі ![]() умовних одиниць після закінченням попереднього кроку
умовних одиниць після закінченням попереднього кроку
|
|
|
|
|
|
| 0 | 5 | 0 | 3,5 | 3,5 |
| 1 | 4 | 2 | 3,2 | 5,2 |
| 2 | 3 | 2,1 | 2,7 | 4,8 |
| 3 | 2 | 2,3 | 2,4 | 4,7 |
| 4 | 1 | 3,5 | 1,7 | 5,2 |
| 5 | 0 | 4 | 0 | 4 |
![]() .
.
Для ![]()
![]() , можливі два умовних оптимальних рівняння:
, можливі два умовних оптимальних рівняння:
– ![]() ;
;
– ![]() .
.
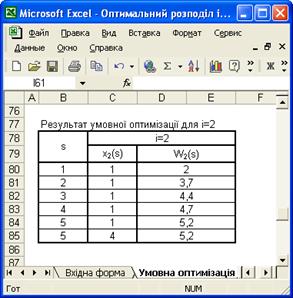
Рисунок 3.2 – Результати умовної оптимізації для другого підприємства
в) Умовна оптимізація для ![]() .
.
Перед першим кроком стан системи відомий. ![]() тисяч умовних одиниць, й умовну оптимізацію слід проводити тільки для цього значення.
тисяч умовних одиниць, й умовну оптимізацію слід проводити тільки для цього значення.
Таблиця 3.8 – Наявність коштів у розмірі ![]() умовних одиниць перед першим кроком
умовних одиниць перед першим кроком
|
|
|
|
|
|
| 0 | 5 | 0 | 5,2 | 5,2 |
| 1 | 4 | 1,5 | 4,7 | 6,2 |
| 2 | 3 | 2 | 4,4 | 6,4 |
| 3 | 2 | 2,5 | 3,7 | 6,2 |
| 4 | 1 | 3 | 2 | 5 |
| 5 | 0 | 3,6 | 0 | 3,6 |
![]() , звідси:
, звідси:
– ![]() ;
;
– ![]() .
.
Вираз (3.9) відображає оптимальний прибуток, що дають три підприємства при інвестуванні в них коштів у розмірі 5 тисяч умовних одиниць, дорівнює 6,4 тисяч умовних одиниць.
![]() . (3.9)
. (3.9)
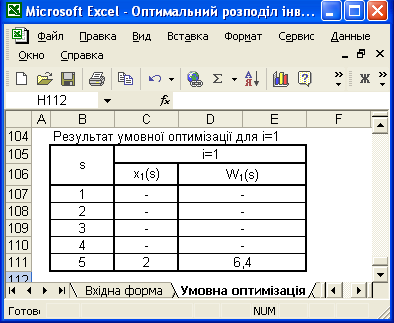
Рисунок 3.3 – Результати умовної оптимізації для першого підприємства
Проведення безумовної оптимізації. Її результати ілюстраційно відображено на рисунку Б.1 додатку Б.
– ![]() ,
, ![]() ,
, ![]() ;
; ![]() .
.
– ![]() по формулі (3.3)
по формулі (3.3) ![]() .
. ![]() ;
; ![]() .
.
– ![]() ,
, ![]() .
. ![]() ;
; ![]() .
.
Отриманий результат – ![]() .
.
Таблиця 3.9 – Результати проведення безумовної оптимізації
|
|
|
|
|
| ||
|
| ||
|
|
| |
|
| ||
|
| ||
|
|
| |
|
| ||
|
|
Таким чином, для отримання максимального прибутку у розмірі 6400 умовних одиниць, необхідно по 2000 умовні одиниці вкласти в перше і третє підприємства і 1000 умовну одиницю – у друге підприємство. Графічно це відображено на графіку В.1 у додатку В.
ВИСНОВКИ
Динамічне програмування – це метод дослідження операцій, на кожному етапі якого можна керувати перебігом досліджуваного процесу та оцінювати якість такого управління. При рішенні задачі динамічного програмування на кожному кроці вибирається керування, що повинне привести до оптимального виграшу. Якщо вважати всі кроки незалежними друг від друга, то оптимальним кроковим управлінням буде те управління, що приносить максимальний виграш саме на даному кроці.
У даній роботі були розглянуті теоретичні аспекти математичного моделювання динамічних систем, основні поняття теорії моделювання, принципи моделювання динамічних систем, моделі і методи прийняття управлінських рішень з урахуванням фактору часу, а також моделі динамічного програмування. Детально вивчені процес постановки задачі динамічного програмування і особливості складання математичної моделі динамічного програмування.
Практичний аналіз динамічного програмування розглядався на прикладі оптимального розподілу інвестицій між підприємствами, мета розподілу полягала у максимізації загального прибутку від інвестування. У результаті практичної реалізації було встановлено, що для отримання максимального прибутку у розмірі 6400 умовних одиниць, необхідно по 2000 умовні одиниці вкласти в перше і третє підприємства і 1000 умовну одиницю – у друге підприємство. Необхідно зазначити, що отримане рішення є лише деяким наближенням до оптимального рішення. Його можна покращити, тобто приблизити до оптимального, взявши менший крок оптимізації, наприклад вкладати у підприємства кошти, кратні 500 умовним одиницям, а отже існує широкий простір для подальшої і більш глибокої роботи.
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
1. Хазанова И.Э. Математическое моделирование в экономике: Учебное пособие. –М.: Издательство БЕК, 1998. – 132 с.
2. Сіднєв С.П., Шарапов О.Д. Математичні методи підвищення якості управлінських рішень: Підручник.-К.: ІЗМН, 1997. – 258 с.
3. Основи комп’ютерних алгоритмів. Динамічне програмування. – http://moodle.ukma.kiev.ua.
4. Вікіпедія. Вільна енциклопедія. Стаття про динамічне програмування. – http://uk.wikipedia.org.
5. Мажукин В.И., Королева О.Н. Математическое моделирование в экономике: Учебное пособие. – М.: Издательство “Флинта” МГУ, 2004. – 232с.
6. Самарский А.А., Михайлов Ф.П. Математическое моделирование. М.: Наука. 1997. – 212 с.
7. Клебанова Т.С., Дубровина Н.А., Полякова О.Ю., Раевнева Е.В., Моделирование экономической динамики: Учебное пособие. – Х.: Издательский дом “ИНЖЭК”, 2005. – 244 с.
Додаток А
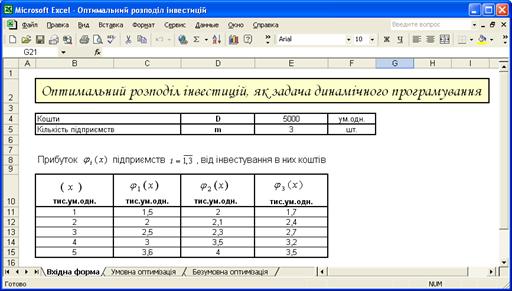
Лист “Вхідна форма”
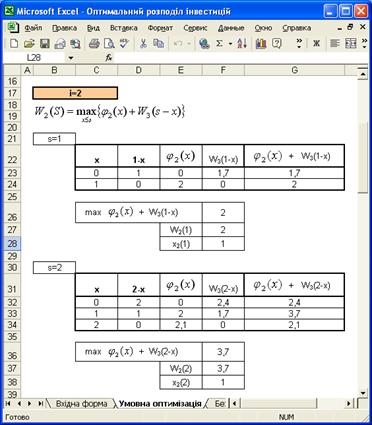
Проведення умовної оптимізації для другого підприємства за умови вкладання 1000 і 2000 умовних одиниць
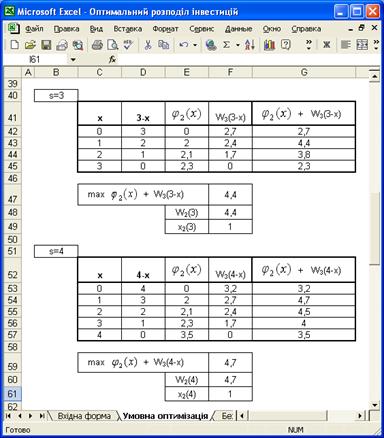
Проведення умовної оптимізації для другого підприємства за умови вкладання 3000 і 4000 умовних одиниць
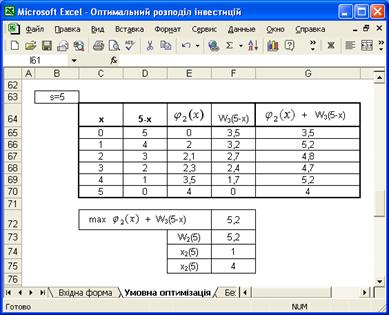
Проведення умовної оптимізації для другого підприємства за умови вкладання 5000 умовних одиниць
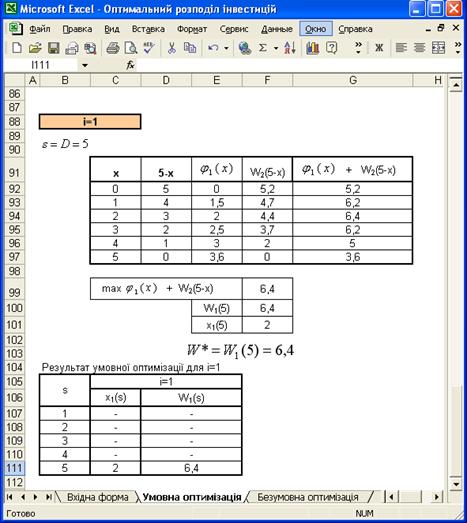
Проведення умовної оптимізації для першого підприємства за умови вкладання 5000 умовних одиниць
Додаток Б
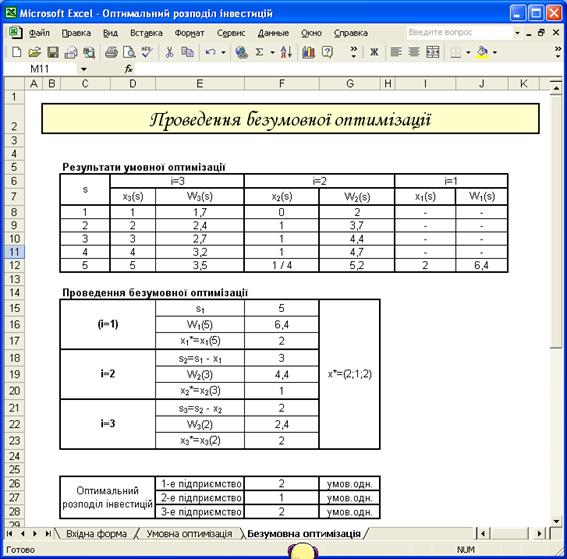
Результати проведення безумовної оптимізації
Додаток В
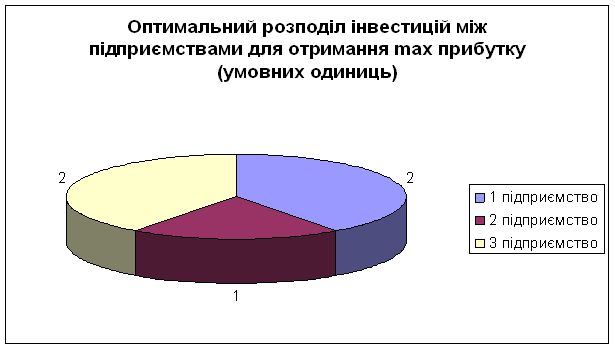
Оптимальний розподіл інвестицій
Похожие работы
... "Баланс" за 2007 – 2008 роки (додаток В); - форма № 2 "Звіт про фінансові результати" за 2007 – 2008 роки (додаток Г). 3 Підвищення ефективності виробництва МКВП "Дніпроводоканал" на підставі методів Економіко-математичного моделювання У грудні 2008 року Дніпропетровський міськвиконком та комунальне Підприємство "Дніпроводоканал", яке знаходиться у власності м. Дніпропетровська ...
... груп за визначений період часу. За допомогою цих даних (статистичної вибірки) ми зможемо описати закон розподілу попиту, на основі якого в подальшому буде ґрунтуватись оптимальне використання складських приміщень. Масштабування даних – переведення з одиниць виміру «пляшки» в «ящики» для зручності розрахунків. Обчислення середніх значень попиту на товари за період та окремо по кожному виду. ...
... ї стійкості по покриттю запасів підприємства ВАТ «Дніпропетровськгаз» у 2005 –2007 роках РОЗДІЛ 3. ЕКОНОМІЧНІ МОДЕЛІ В ПРОГНОЗУВАННІ ПОКАЗНИКІВ ФІНАНСОВОЇ ЗВІТНОСТІ ПІДПРИЄМСТВА Прогнозування фінансово-економічних результатів операційної діяльності ВАТ «Дніпропетровськгаз» в курсовому дослідженні виконано з застосуванням кореляційно-регресійних економіко-математичних моделей, які спираються ...
... фінансово-господарської і зовнішньоекономічної діяльності за 2008 рік. Порівняння основних показників фінансово-господарської і зовнішньоекономічної діяльності ТОВ «Центр ділових інвестицій» за 2008 рік і планованих відповідно до розробленої диверсифікованої стратегії розвитку приведені в таблиці 3.8. Таблиця 3.8 Показники оцінки економічної ефективності диверсифікованої стратегії розвитку ...


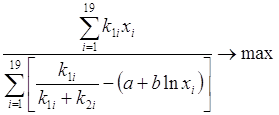

0 комментариев