Навигация
2.2 Выборочная дисперсия
По выборочным данным важно знать не только выборочное среднее, но и разброс выборочных значений около выборочного среднего. Если выборочное среднее является оценкой генерального среднего, то выборочная дисперсия должна быть оценкой генеральной дисперсии. Выборочная дисперсия 
для выборки, состоящей из случайных величин 
определяется следующим образом
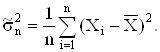
Используя это представление выборочной дисперсии, найдем ее математическое ожидание
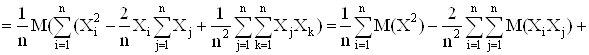
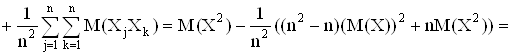
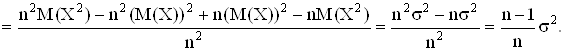
Таким образом мы получили, что 
Это значит, что выборочная дисперсия является смещенной оценкой генеральной дисперсии. Чтобы получить несмещенную оценку, нужно величину умножить на 
тогда выборочная дисперсия имеет вид
Итак мы получили следующий результат. Если в результате n независимых измерений случайной величины Х с неизвестным математическим ожиданием и дисперсией нам нужно по полученным данным определить эти параметры, то следует пользоваться следующими приближенными оценками
В случае, если известно математическое ожидание генеральной совокупности mx, то выборочную дисперсию следует вычислять по формуле
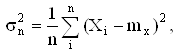
которая также является несмещенной оценкой.
3. Статистический ряд. Статистическая функция распределения
Пусть имеются результаты измерения случайной величины Х с неизвестным законом распределения, которые представлены в виде таблицы:
| i | 1 | 2 | . . . | n |
| xi | x1 | x2 | . . . | xn |
Такую таблицу называют статистическим рядом. Статистический ряд представляет собой первичную форму записи статистического материала и он может быть обработан различными способами. Одним из таких способов обработки является построение статистической функции распределения случайной величины Х.
Статистической (эмпирической) функцией распределения F*(x) называется закон изменения частоты события X < x в данном статистическом материале, то есть
Для того, чтобы найти значение статистической функции распределения при данном х, надо подсчитать число опытов, в которых случайная величина Х приняла значения меньше, чем х, и разделить на общее число произведенных опытов. Полученная таким образом статистическая функция распределения является очень грубым приближением функции распределения F(x) случайной величины Х и в таком виде не используется на практике. Она носит в каком-то смысле качественный характер, из которого можно выдвинуть гипотезу о законе распределения случайной величины Х. При увеличении числа опытов (n ®¥) F*(x) по вероятности сходится к F(x). Однако, с увеличением n построение F*(x) становится очень трудоемкой операцией. Поэтому на практике часто бывает удобно пользоваться статистической характеристикой, которая приближается к плотности распределения.
Похожие работы
... технический университет радиоэлектроники Кафедра ПОЭВМ Комплексная курсовая работа по курсу «Вероятностные процессы и математическая статистика в автоматизированных системах» Тема: «Провести экономическую оценку эффективности работы предприятия. Провести долгосрочное планирование работы методом множественной линейной регрессии. Построить математическую модель повышения эффективности работы». ...
... опираться на теорию множеств, математическую логику, теорию алгоритмов. На основе применения «неколичественного» математического аппарата в теоретическом языкознании сформировалось направление, условно называемое комбинаторной лингвистикой – в ней используются методы математической статистики теории вероятностей, теории информации, математического анализа Современные инструментальные методы ...
... среднее квадратическое отклонение по размаху выгодно при малом числе измерений: при числе вариант не более 20 (а это, как известно, имеет большое значение для сравнительных педагогических экспериментов, в которых, как правило, участвует ограниченное количество исследуемых). Величина среднего квадратичного отклонения зависит от величины колебаний вариант: чем больше амплитуда различий между ...
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...
0 комментариев