Навигация
Математичні моделі на рівні функціональних ланок системи
2.2 Математичні моделі на рівні функціональних ланок системи
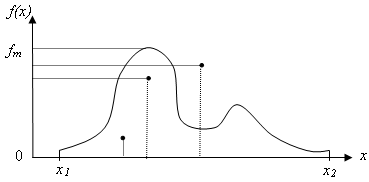
Розглянемо деякі особливості математичного опису функціональних ланок на прикладі лінійних інерційних ланок. Для їх опису часто використовуються: імпульсна характеристики, перехідна характеристики, комплексна частотна характеристики ланки.
При використанні імпульсної характеристики лінійної інерційної ланки ![]() вихідний сигнал
вихідний сигнал ![]() через вхідний сигнал
через вхідний сигнал ![]() записується у вигляді інтегралу Дюамеля
записується у вигляді інтегралу Дюамеля
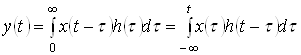 . (6)
. (6)
Для опису лінійної інерційної ланки може бути також використана перехідна характеристика, що зв'язана з імпульсною характеристикою наступним співвідношенням
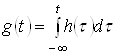 . (7)
. (7)
Поряд з часовим описом може також використовуватися частотний опис ланки у вигляді частотної характеристики (частотного коефіцієнту передачі) ![]() , яка однозначно зв'язана з імпульсною характеристикою
, яка однозначно зв'язана з імпульсною характеристикою ![]() перетворенням Фур'є
перетворенням Фур'є
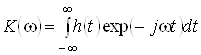 . (8)
. (8)
При цьому спектр вихідного сигналу визначається через спектр вхідного сигналу та частотну характеристику ланки
![]() . (9)
. (9)
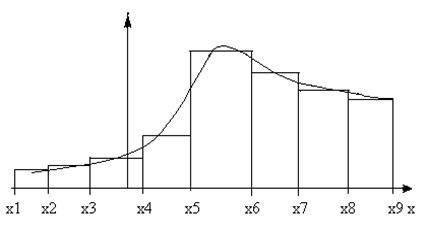
При переході до дискретного часу та кінечного інтервалу спостереження сигналів зв'язок між входом і виходом лінійної системи описується дискретною згорткою, яка фактично визначає роботу нерекурсивного цифрового фільтру
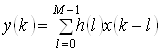 . (10)
. (10)
де ![]() - відліки вхідного дискретного сигналу,
- відліки вхідного дискретного сигналу, ![]() - відліки імпульсної характеристики.
- відліки імпульсної характеристики.
У випадку спектрального зображення сигналів відповідні перетворення у функціональних ланках виконуються згідно (9). Для сигналів з дискретним часом спектр визначається через дискретне перетворення Фур'є (ДПФ)
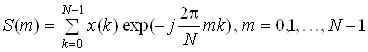 . (11)
. (11)
Відліки спектру сигналу обчислюються для дискретних значень частот
![]() . (12)
. (12)
Перехід до відліків спектру ![]() сигналу проводиться за допомогою оберненого дискретного перетворення Фур'є
сигналу проводиться за допомогою оберненого дискретного перетворення Фур'є
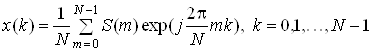 . (12)
. (12)
При моделюванні сигналів значної розмірності ![]() доцільно використовувати швидкі алгоритми перетворення Фур'є, які дають можливість суттєво зменшити обсяг обчислення на ЕОМ при виконанні прямого та оберненого ДПФ.
доцільно використовувати швидкі алгоритми перетворення Фур'є, які дають можливість суттєво зменшити обсяг обчислення на ЕОМ при виконанні прямого та оберненого ДПФ.
В системах зв'язку використовуються багато різних видів лінійних та нелінійних, інерційних та безінерційних ланок. Для прикладу можна навести приклади типових ланок: генератори сигналів заданої форми; амплітудний, фазовий, частотний модулятор та детектор; інтегратор; корелятор; низькочастотний, високочастотний, полосовий, узгоджений фільтр; перемножувач частоти сигналів та інші. В табл. 1 приведено опис деяких функціональних ланок. Для описування ланок необхідно знати вид функційного перетворення ![]() . Якщо вид функціонального перетворення досить складний, його апроксимують простими функціями. В ряді випадків цю функцію перетворення розкладають в ряд Фур'є, Тейлора, а потім виконують необхідні перетворення.
. Якщо вид функціонального перетворення досить складний, його апроксимують простими функціями. В ряді випадків цю функцію перетворення розкладають в ряд Фур'є, Тейлора, а потім виконують необхідні перетворення.
Слід зазначити, що при моделюванні можуть бути використані також ймовірнісні моделі функціональних ланок та системи в цілому, що описують функціювання у реальних умовах роботи систем зв’язку.
Таблиця 1 - Деякі основні типи функційних ланок
| Назва ланки | Оператор перетворення | Назва перетворення | Зображення на функційній схемі |
| 1 | 2 | 3 | 4 |
| 1. Лінійні безінерційні ланки |
| Повторення інвертування підсилення | |
|
|
| затримка сигналу на інтервал інтегрування диференціювання фільтрування | |
|
|
| Нелінійне функційне перетворення | |
|
|
| Генерування сигналу | |
|
|
| моделювання сигналу-носія |
Похожие работы
... і провести моделювання за початковими даними; · розробити програмне забезпечення для статистичного моделювання сітьового графіка за початковими даними; · зробити висновки по роботі та досягнутим результатам. 1 ЗАГАЛЬНА ХАРАКТЕРИСТИКА ПРЕДМЕТНОЇ ОБЛАСТІ 1.1 Дослідження процесу побудови судна 1.1.1 Аналіз процесу побудови судна як об’єкта ...
... ійна діяльність не є самоціллю. Тому, визначаючи місце і роль закону пропорційності, слід орієнтуватися в першу чергу на основний закон організації. Досягнення пропорційності як би забезпечує саму можливість отримання синергетичного ефекту. 3. ПРИНЦИПИ ОРГАНІЗАЦІЇ 3.1 Сутність і зміст принципів організації В попередньому розділі нами встановлено, що пізнання законів організації дозволя ...
... общин, де кожний буде зобов'язаний трудитися. М.А. Бакунін дотримувався ідей анархізму, бачивши у владі причину експлуатації. Один з феноменів російської науки - плідна розробка ідей економіко-математичного моделювання, заснована на базі як „чистих” математиків, що направили свої зусилля в економіку, так і розробок професійних економістів. Перші російські економісти-математики (Ю.Г. Жуковській, ...
... практ. конф. Хмельницький, 17 травня 2007 р. – Хмельницький: Хмельницький університет управління та права, 2007. – С. 206-209. – 0,13 друк. арк. АНОТАЦІЯ Корепанов О.С. Статистичне прогнозування кон’юнктури аграрного ринку в Україні. – Рукопис. Дисертація на здобуття наукового ступеня кандидата економічних наук за спеціальністю 08.00.10 – Статистика. - Державна академія статистики, обліку та ...
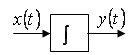
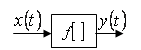
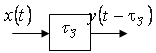 2. Лінійні інерційні ланки
2. Лінійні інерційні ланки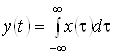
 3. Нелінійні безінерційні ланки
3. Нелінійні безінерційні ланки
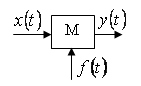 5. Модулятор
5. Модулятор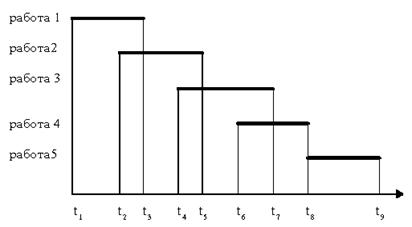
0 комментариев