Математичні моделі випадкових сигналів

3.3 Математичні моделі випадкових сигналів

Однак, крім детермінованих сигналів і перетворень, при моделюванні систем зв’язку виникає необхідність реалізувати на ЕОМ різного роду випадкові елементи - випадкові величини, випадкові сигнали і поля. Зокрема, у каналах зв'язку діють випадкові завади різного типу: флуктуаційні та імпульсні; адитивні та мультиплікативні, вузькосмугові та широкосмугові; активні та пасивні. Вони відрізняються структурою та механізмом виникнення, а також своїми імовірнісними характеристиками. Окрім того повідомлення, як правило, також носять стохастичний характер. Тому сигнали, що передаються та приймаються в системах зв’язку в загальному випадку треба розглядати як випадкові сигнали. Для побудови їх математичних моделей необхідно використовувати ймовірнісні моделі, тобто випадкові процеси з різними імовірнісними характеристиками. Випадкові процеси описуються математичним апаратом, який суттєво відрізняється від апарату детермінованих сигналів. Сучасний математичний аппарат, який використовується для опису випадкових елементів, базується на теорії множин, теорії міри, теорії функцій дійсної змінної та функціональному аналізі.

Cигнал як фізичний процес, що використовується для передавання інформації в системах зв'язку, може описуватися випадковою функцією. Випадкова функція - це суттєво інший випадковий математичний об'єкт порівняно з детермінованою функцією. Її можна визначити як параметричну множину випадкових величин, що задовольняє певні умови

, (22)

де  - параметр з множини ;  - елементарна подія з множини елементарних подій .

Параметр  може мати різне тлумачення. Якщо  - має сенс часу , то випадкова функція  - це випадковий процес

. (23)

Коли  - зліченна множина , тоді функцію (23) називають випадковим процесом з дискретним часом або часовою послідовністю. У кожному випадку маємо множину випадкових величин, заданих на ймовірнісному просторі , де  - -алгебра;  - імовірнісна міра.

На основі (23) може розглядатися декілька визначень випадкового процесу. Так множину (23) можна розглядати по різному: як упорядковану відносно параметра  сукупність випадкових величин; як сукупність числових функцій часу, кожна з яких розглядається як елементарна подія; як функцію, що залежить від двох змінних .

Існує протиріччя між необхідністю повного опису випадкового процесу та достатньою простотою, яка визначається необхідністю розв’язання прикладних задач. Тому при розв’язанні багатьох прикладних задачах зв’язку ідуть на спрощений опис випадкового процесу, зокрема, в рамках кореляційної теорії, коли використовуються тільки дві моментні функції випадкового процесу – кореляційна функція та математичне сподівання. Кореляційна теорія випадкових процесів містить у собі декілька зображень процесів в інтегральному вигляді та у вигляді рядів. Це, насамперед, відповідні поширення на випадкові процеси інтегрального перетворення Фур’є, рядів Фур’є і Котельникова та зображення аналітичних та вузькосмугових сигналів, що широко використовуться для зображення детермінованих сигналів.

Кореляційна теорія набула широкого поширення, проте у галузі зв’язку існують задачі, які не можуть бути розв’язані в її рамках. Такими є задачі оптимального приймання сигналів, задачі теорії інформації, декодування сигналів. Для їх розв’язання необхідно застосовувати повніший опис випадкового процесу з використанням функцій розподілу. Розглянемо деякі класи випадкових процесів, що можуть бути використовані в ролі математичних моделей реальних фізичних процесів у системах зв’язку.

Вузькосмугові випадкові процеси. За аналогією з описом вузькосмугових детермінованих сигналів може бути використана математична модель у виді вузькосмугового випадкового процесу

(24)

де  - це комплексна обвідна випадкового процесу. При цьому аналогічно до детермінованих сигналів розглядаються квадратурні складові , які також є випадковими процесами. Через квадратурні складові вводяться поняття амплітуди та фази випадкового процесу

.

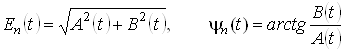Математична модель у вигляді вузькосмугового випадкового процесу може бути використана, наприклад, для описування флуктуаційної модульованих випадковим повідомленням сигналів, а також завади у вузькій смузі частот існування сигналів, що передаються.

Білі шуми. Одним із найбільш відомих і поширених класів випадкових процесів є білий шум. Білий шум – це випадковий процес з незалежними або некорельованими значеннями. Для дискретного часу білий шум - це послідовність незалежних або некорельованих випадкових величин. В залежності від імовірностних властивостей розглядають стаціонарний і нестаціонарний, гаусовий і негаусовий білий шум. Згідно з означенням білого шуму, він повністю визначається через одновимірні функції чи щільності розподілу. Зокрема, багатовимірна щільність ймовірності визначається як добуток одновимірних щільностей ймовірності.

Наприклад, для стаціонарного білого шуму з дискретним часом багатовимірна щільність ймовірності визначається у вигляді

. (24)

Білий шум є - корельованим (у розумінні -функції Кронекера) випадковим процесом, кореляційна функція якого має вигляд

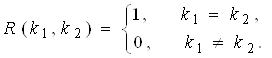(25)

На підставі теореми Вінера-Хінчина спектральна густина білого шуму з дискретним часом рівномірна у смузі частот  і має значення .

Для описування реальних фізичних процесів в системах зв'язку використовують також "негаусові" білі шуми - випадкові процеси, які мають такі ж властивості кореляційної функції та спектральної щільності, а щільність розподілу ймовірностей відрізняється від гаусової.

Математична модель у виді білого шуму може бути використана для описування завад у системах зв'язку.

Марківські процеси. Модель у виді білих шумів не враховує зв’язків суміжних значень, які розглядаються як статистично незалежні або некорельовані. Модель у виді марківських процесів враховує такі зв’язки, які поширюються тільки на один крок (або на фіксоване число кроків). Це відповідно прості та багатозв’язні марківські процеси.

Зокрема, випадковий процес з дискретним часом називають простим стаціонарним марківським процесом, багатовимірна щільність розподілу ймовірностей якого визначається одновимірною щільністю ймовірностей та щільністю ймовірностей переходів

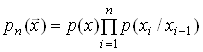. (26)

Співвідношення (26) визначає марківську властивість випадкового процесу.

Для описування реальних процесів у системах зв'язку використовується також математична модель у вигляді марківських ланцюгів - випадкових процесів з дикретним часом, що приймають зчисленну множину значень. При цьому замість щільності ймовірності, притаманної для марківського процесу, основні характеристики процесу описуються ймовірностями відповідних подій. Марківська властивість для таких процесів описується співвідношенням

, (27)

де .

Марківські ланцюги можуть бути використані для математичного опису джерела дискретних, зокрема, телеграфних повідомлень, а також процесів обслуговуванння у системах комутації.

Лінійні випадкові процеси. Існують різні означення лінійних випадкових процесів. Розглянемо одне із них, що основане на інтегральному зображенні

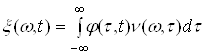, (28)

де  - імпульсна характеристика лінійного фільтру;

 - білий шум.

Тут лінійний процес  розглядається як перетворення білого шуму  лінійним фільтром з імпульсною характеристикою . При цьому можуть бути одержані лінійні процеси з різними ймовірнісними характеристиками, які визначаються видом функції , а також видом білого шуму. Зокрема, білий шум може бути гаусовим, пуасоновим, їх сумішшю або іншими білими шумами. Лінійний фільтр у виразі (28) має назву формуючого фільтра, а білий шум - породного процесу.Для лінійних процесів з дискретним часом математична модель визначається відповідним співвідношенням

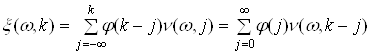(29)

де  - дискретні відліки імпульсної характеристики фільтру,  - білий шум з дискретним часом.

Лінійний процес можна також зобразити у виді авторегресії на минулі значення. При цьому можна одержати процеси авторегресії, ковзного середнього та змішані процеси авторегресії та ковзного середнього. Зокрема, процес авторегресії -го порядку описується рівнянням

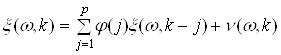. (30)

Лінійні процеси можуть бути використані як математичні моделі, зокрема, при описі джерела мовних повідомлень, кодера мовних повідомлень, джерела корельованих завад.

Існує також багато інших математичних моделей, що мають свої характерні властивості і дають можливість враховувати особливості різних фізичних процесів в системах зв'язку при їх моделювані на ЕОМ. Зокрема, це математичні моделі, що описують негаусів характер сигналів за допомогою сумішей розподілу, сукупності моментних та кумулянтних функцій, а також нестаціонарний характер сигналів - за допомогою періодично-корельованих випадкових процесів.

Систематизований опис різних ймовірносних моделей приведений у роботах. Деякі специфічні математичні моделі сигналів описані у наступному розділі, де розглядається алгоритми моделювання на ЕОМ різних випадкових елементів - випадкових величин, векторів та випадкових процесів.

Похожие работы

Статистичне моделювання сітьового графіка побудови судна

Скачать

70410

3

11

... і провести моделювання за початковими даними; ·              розробити програмне забезпечення для статистичного моделювання сітьового графіка за початковими даними; ·              зробити висновки по роботі та досягнутим результатам. 1 ЗАГАЛЬНА ХАРАКТЕРИСТИКА ПРЕДМЕТНОЇ ОБЛАСТІ   1.1 Дослідження процесу побудови судна   1.1.1 Аналіз процесу побудови судна як об’єкта ...

Основні положення теорії організації. Закони та основні принципи організації

Скачать

67152

0

5

... ійна діяльність не є самоціллю. Тому, визначаючи місце і роль закону пропорційності, слід орієнтуватися в першу чергу на основний закон організації. Досягнення пропорційності як би забезпечує саму можливість отримання синергетичного ефекту. 3. ПРИНЦИПИ ОРГАНІЗАЦІЇ 3.1 Сутність і зміст принципів організації В попередньому розділі нами встановлено, що пізнання законів організації дозволя ...

Економіко–математичне моделювання

Скачать

140123

0

3

... общин, де кожний буде зобов'язаний трудитися. М.А. Бакунін дотримувався ідей анархізму, бачивши у владі причину експлуатації. Один з феноменів російської науки - плідна розробка ідей економіко-математичного моделювання, заснована на базі як „чистих” математиків, що направили свої зусилля в економіку, так і розробок професійних економістів. Перші російські економісти-математики (Ю.Г. Жуковській, ...

Статистичне прогнозування кон’юнктури аграрного ринку в Україні

Скачать

52946

4

3

... практ. конф. Хмельницький, 17 травня 2007 р. – Хмельницький: Хмельницький університет управління та права, 2007. – С. 206-209. – 0,13 друк. арк. АНОТАЦІЯ   Корепанов О.С. Статистичне прогнозування кон’юнктури аграрного ринку в Україні. – Рукопис. Дисертація на здобуття наукового ступеня кандидата економічних наук за спеціальністю 08.00.10 – Статистика. - Державна академія статистики, обліку та ...