Навигация
Математичний опис сигналів при моделюванні систем зв’язку
29310
знаков
1
таблица
0
изображений
3. Математичний опис сигналів при моделюванні систем зв’язку
При моделюванні систем зв’язку важливим є опис реальних сигналів і завад їх математичними моделями, що базуються на основних положеннях теорії сигналів. В системах зв'язку зустрічаються різного виду детерміновані та випадкові сигнали. Зокрема, це такі сигнали: сигнал-повідомлення 
(низькочастотний, як правило, випадковий сигнал), сигнал-переносчик 
(як правило, детермінований сигнал у вигляді гармонічного коливання), модульований сигнал 
(як правило, високочастотний вузькосмуговий сигнал), завада 
(як правило, випадковий широкосмуговий сигнал). Таким чином, для математичного опису сигналів та завад у системах зв’язку необхідно використовувати різні детерміністські та ймовірнісні моделі. Розглянемо деякі математичні моделі детермінованих та випадкових сигналів.
3.1 Математична модель вузькосмугових детермінованих сигналів
Якщо переносчиком є гармонійний сигнал, то модульований сигнал може розглядатися при певних умовах як вузькосмуговий сигнал і тоді можна використати відповідне зображення сигналу у виді 
,
де 
- оператор модуляції гармонійного сигналу-переносчика;
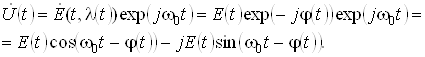(13)
Цей вираз дає можливість одержати зображенням сигналу за допомогою квадратурних компонент
, (14)
де 
- квадратурні компоненти.
Через квадратурні компоненти можна записати вираз для амплітуди та фази комплексної обвідної сигналу у виді:
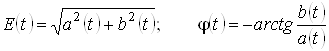. (15)
Конкретний вид комплексної обвідної модульованого сигналу залежить від вибраного вигляду оператора модуляції 
та вигляду повідомлення
. (16)
При амплітудній модуляції буде мати місце зміна амплітуди комплексної обвідної, при кутовій (частотній або фазовій) модуляції - зміна фази відповідно до переданого повідомлення. Наприклад, при амплітудній модуляції вираз для амплітуди обвідної визначається так
, (17)
де 
- коефіцієнт амплітудної модуляції.
Зображення сигналів через квадратурні компоненти, зокрема, співвідношення (15) дає можливість також будувати математичні моделі демодуляторів систем зв’язку з різними видами модуляції.
3.2 Математичні моделі низькочастотних детермінованих сигналів
Для опису періодичних сигналів широко використовується ряд Фур'є
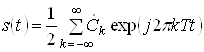, (18)
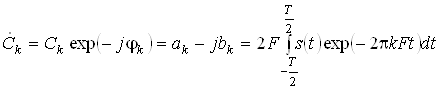, (19)
де 
– період повторення сигналу, 
.
Спектральне зображення неперіодичних абсолютно інтегрованих сигналів визначається перетворенням Фур'є
, 
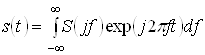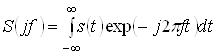. (20)
На практиці часто для зображення сигналів використовують узагальнений ряд Фур'є
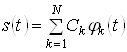, (21)
де 
- ортонормована система базисних функцій;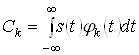 
- коефіцієнти розкладу.
Поряд з базисом тригонометричних функцій використовуються також базисні функції Лежандра, Лагерра, Ерміта, Чебишова, Уолта, Хаара та інші.
Таким чином, моделювання детермінованих сигналів та їхніх перетворень у різних ланках системи зводиться до обчислення на ЕОМ детермінованих функцій, заданих у дискретні моменти часу. Як правило, це не викликає складності ні принципового, ні обчислювального характеру при проведенні моделювання систем на сучасних ЕОМ.
Похожие работы
... і провести моделювання за початковими даними; · розробити програмне забезпечення для статистичного моделювання сітьового графіка за початковими даними; · зробити висновки по роботі та досягнутим результатам. 1 ЗАГАЛЬНА ХАРАКТЕРИСТИКА ПРЕДМЕТНОЇ ОБЛАСТІ 1.1 Дослідження процесу побудови судна 1.1.1 Аналіз процесу побудови судна як об’єкта ...
... ійна діяльність не є самоціллю. Тому, визначаючи місце і роль закону пропорційності, слід орієнтуватися в першу чергу на основний закон організації. Досягнення пропорційності як би забезпечує саму можливість отримання синергетичного ефекту. 3. ПРИНЦИПИ ОРГАНІЗАЦІЇ 3.1 Сутність і зміст принципів організації В попередньому розділі нами встановлено, що пізнання законів організації дозволя ...
... общин, де кожний буде зобов'язаний трудитися. М.А. Бакунін дотримувався ідей анархізму, бачивши у владі причину експлуатації. Один з феноменів російської науки - плідна розробка ідей економіко-математичного моделювання, заснована на базі як „чистих” математиків, що направили свої зусилля в економіку, так і розробок професійних економістів. Перші російські економісти-математики (Ю.Г. Жуковській, ...
... практ. конф. Хмельницький, 17 травня 2007 р. – Хмельницький: Хмельницький університет управління та права, 2007. – С. 206-209. – 0,13 друк. арк. АНОТАЦІЯ Корепанов О.С. Статистичне прогнозування кон’юнктури аграрного ринку в Україні. – Рукопис. Дисертація на здобуття наукового ступеня кандидата економічних наук за спеціальністю 08.00.10 – Статистика. - Державна академія статистики, обліку та ...
0 комментариев