Навигация
1.3 Ошибка выборки
Все ошибки выборочного наблюдения подразделяются на ошибки выборки (случайные); ошибки, вызванные отклонением от схемы отбора (неслучайные); ошибки наблюдения (случайные и неслучайные). Плохо, когда ошибка выборки превышает допустимый размер погрешности, но слишком высокая точность также подозрительна и, как правило, свидетельствует об ошибках отбора. К неслучайным ошибкам приводят ошибки отбора. Так бывает, если объективный отбор подменяется «удобной» выборкой. Например, когда появляются добровольные респонденты — те, кто сами предлагают, чтобы их опросили. Очевидно, что характеристики таких добровольцев и недобровольцев могут быть различны и это приведет к ошибочному заключению о генеральной совокупности. Такая же опасность возникает при замене по какой-либо причине единиц, попавших в выборку, другими единицами (например, вместо отобранного домохозяйства, где в момент прихода интервьюера никто не открыл дверь, был проведен опрос в соседней квартире или интервьюер встретил решительный отказ участвовать в опросе и был вынужден пойти на замену домохозяйства). Как отмечает социолог В. И. Паниотто, систематические ошибки представляют собой некоторое постоянное смещение, которое не уменьшается с увеличением числа опрошенных и вызваны недостатками и просчетами в системе отбора респондентов. Если, например, для изучения общественного мнения жителей города в архитектурном управлении получить сведения о жилом фонде и из всех имеющихся в городе квартир отобрать случайным образом 400, а затем предложить интервьюерам опросить всех, кого они застанут в момент посещения в этих квартирах, то полученные данные не будут репрезентативны. Допущена систематическая ошибка: более подвижная часть населения попадает в выборку в меньшей пропорции, а менее подвижная — в большей пропорции, чем в генеральной совокупности.
Таким образом, с вероятностью 0,95 можно утверждать, что средняя продолжительность расчетов предприятия данного треста с кредиторами составляет не менее 26,7 дня и не более 29,7 дня. Ошибка выборки для выборочной относительной величины (доли) определяется аналогично. Дисперсию относительной величины определим по данным выборки:
Пример. По данным выборочного изучения 100 платежных документов предприятий одного треста оказалось, что в шести случаях сроки расчетов с кредиторами были превышены. С вероятностью 0,954 требуется установить доверительный интервал доли платежных документов треста без нарушения сроков:
1.4 Влияние вида выборки на величину ошибки выборки
Как указывалось в подразд. 7.2, при проведении выборочного наблюдения используются различные способы формирования выборочной совокупности: случайный отбор — повторный или бесповторный, механический, серийный, типический. Вид выборки влияет на величину ошибки выборки. При бесповторном отборе формулы средней ошибки выборки (7.4) и (7.14) дополняются множителем Величина ошибки районированной выборки меньше величины ошибки простой (нерайонированной выборки). Часто используется сочетание районированного отбора с отбором сериями. Такой вид выборки обеспечивает преимущества в организации выборки и уменьшение ошибки выборки. Дисперсия такой выборки представляет среднюю из межсерийных дисперсий для каждого у'-го района: Оборачиваемость запасов рассчитывается делением продолжительности периода (полгода) на среднюю продолжительность одного периода оборота запасов. Очевидно, что чем скорее оборачиваются запасы, тем выше их отдача.
Коэффициент покрытия рассчитывается как отношение суммы всех источников покрытия запасов к стоимости запасов. Еслизначение этого показателя меньше единицы, то текущее финансовые показатели предприятий легкой промышленности крупного города за I полугодие 2001 г. т.е. таких предприятий должно быть не меньше 2% и не больше 28%. Фактически в генеральной совокупности их оказалось 20% общего числа предприятий, т.е. выборка дает репрезентативный результат и по этому показателю.
Выполненная выборка формировалась как простая бесповторная механическая. Однако наверняка статистик будет стремиться учесть структуру генеральной совокупности, поэтому более естественной была бы выборка, учитывающая выделение предприятий разных форм собственности. Тогда выборка должна быть районированной.
Пример. Генеральная совокупность состоит из 11 государственных предприятий, 36 частных, 13 смешанных. В выборке эти пропорции соблюдаются следующим образом: отобраны по 4 предприятия государственных и смешанных и 12 частных.
Таким образом, использование многоступенчатой выборки улучшает организацию выборки, но увеличивает ее ошибку. Кроме рассмотренных применяется многофазовая выборка, когда одни сведения собираются по всем единицам выборки, а другие — только по подвыборке из первоначальной выборки.
При периодическом повторении выборочных обследований с целью изучения динамики явлений применяются либо независимые выборки — через определенные промежутки времени отбор каждый раз проводится независимо от предыдущих выборок; либо фиксированные выборки — в этом случае повторные обследования проводятся по одной и той же выборке. В связи с тем, что в фиксированной выборке могут происходить изменения (прежде всего за счет выбытия единиц), практикуют периодическую адаптацию фиксированной выборки к происходящим изменениям. Чаще для целей изучения динамики используется промежуточный вариант ротационная выборка (частичное замещение). При этом нужно следовать определенному плану замещения, например, каждый раз замещать четверть выборки, тогда каждая первоначально отобранная единица останется в четырех следующих друг за другом выборках.
Названные виды выборок ориентированы на отбор конкретных материальных явлений. Помимо них следует назвать как особыйвид выборки метод моментных наблюдений. Сущность этого метода состоит в периодической фиксации состояний наблюдаемых единиц в отобранные моменты времени. Расчет объема такой выборки дает количество моментов. Этот вид выборочного наблюдения применяется при изучении использования производственного оборудования либо рабочего времени (подразд. 7.7).
Похожие работы
... 2272 9862 МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Санкт-Петербургский государственный университет аэрокосмического приборостроения СТАТИСТИКА Выборочные наблюдения Методические указания к практическим занятиям Санкт-Петербург 1999 Составитель Н.А. Богородская Рецензент кандидат экономических наук доцент Л.Г.Фетисова Методические ...
... mx , соответствующий доверительной вероятности b. Действительно, так как то Пользуясь таблицей значений интеграла по значению b найдем величину а следовательно, и сам доверительный интервал le = 2. Проверка статистических гипотез Принятие решения о параметрах генеральной совокупности играет исключительно важную роль на практике. Рассмотрим вопрос о принятии решения на примере ...
... 0,997 С вероятностью 0,997 можно утверждать, что средний разряд рабочих механического цеха находится в пределах , . 4 Определение необходимой численности выборки В практике проведения выборочного наблюдения возникает потребность в определении численности выборки, которая необходима для обеспечения определенной точности расчета генеральных характеристик – средней и доли. Формально вопрос ...
... данных и по внедрению накопленного арсенала современных методов прикладной статистики. По нашему мнению, широкого внедрения заслуживают, в частности, методы многомерного статистического анализа, планирования эксперимента, статистики объектов нечисловой природы. Очевидно, рассматриваемые работы должны быть плановыми, организационно оформленными, проводиться мощными самостоятельными организациями и ...
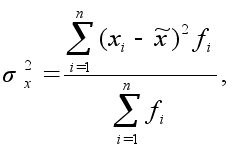
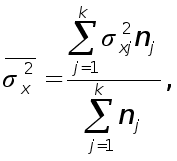
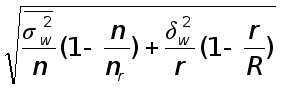
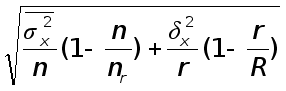

0 комментариев