Навигация
Погрешности вычислений на ЭВМ
Содержание
1. Источники и виды погрешностей результата вычислительной задачи
2. Абсолютные и относительные погрешности
3. Правила записи приближенных чисел
4. Погрешность суммы и разности приближенных чисел
5. Погрешности произведения и частного приближения чисел погрешности
6. Погрешность функции
7. Погрешность функции нескольких переменных
8. Обратная задача теории погрешностей
Список литературы
1. Источники и виды погрешностей результата вычислительной задачи
Погрешности вычислений на ЭВМ
Цель работы: изучение влияния различных видов погрешностей на результаты вычислений на ЭВМ
При решении задачи на ЭВМ практически невозможно получить точное решение. Получаемое численное решение почти всегда содержит погрешность, т.е. является приближенным. Погрешности решения задач на ЭВМ объясняются следующими причинами:
1) математическая модель задачи является приближенным описанием реального объекта или процесса. Поэтому получаемые результаты также всегда будут приближенными, а их погрешности зависят от степени адекватности моделей реальному объекту или процессу;
2) исходные данные при решении вычислительной задачи, как правило, содержат погрешности. Это объясняется тем, что исходные данные получают в результате экспериментов, наблюдений, измерений или в результате решения вспомогательных задач;
3) применяемые для решения вычислительных задач методы в большинстве случаев являются приближенными, так как получить аналитическое решение задачи обычно не удается;
4) использование ЭВМ вносит ошибки, которые появляются при вводе-выводе данных в процессе вычислений.
С учетом указанных выше причин погрешность решения вычислительной задачи на ЭВМ складывается из трех составляющих:
- неустранимая погрешность;
- погрешность метода;
- вычислительная погрешность.
Неустранимая погрешность соответствует первым двум причинам и единственный способ уменьшить эту погрешность заключается в переходе к более точной модели или в использовании более точных входных данных.
Погрешность метода определяется третьей причиной, причем появление этой погрешности практически неизбежно при любых вычислениях.Вычислительная погрешность возникает в основном из-за округления чисел при вводе-выводе, а также при выполнении арифметических операций в ЭВМ. Это обусловлено ограниченной разрядностью ЭВМ и особенностями представления данных в памяти машины.
2. Абсолютные и относительные погрешности
Рассмотрим числовые характеристики погрешностей. Будем считать, что результат решения задачи на ЭВМ является приближенным числом.
Пусть А – точное число, которое может быть и неизвестным. Тогда приближенным числом а будем называть такое число, которое незначительно отличается от точного А и заменяет его в вычислениях. При этом говорят, что число а является приближением числа А, что обозначается как А » а.
Например, пусть p - точное число. Тогда различные приближения можно задать следующим образом:
![]() ;
; ![]() ;
; ![]() .
.
Разность А - а между точным числом А и его приближением а называется погрешностью или ошибкой приближенного числа а.
Поскольку возможно, что а > А или а < А вводится понятие абсолютной погрешности приближенного числа, которая обозначается как Dа =½А - а½.
Возможны два случая вычисления абсолютной погрешности:
1) когда точное число известно, например
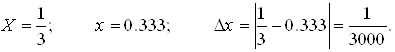 2) если точное число не известно, то для оценки погрешности приближения используется понятие предельной абсолютной погрешности:
2) если точное число не известно, то для оценки погрешности приближения используется понятие предельной абсолютной погрешности: ![]() или
или ![]() .
.
Если предельная абсолютная погрешность задана, то ее значение позволяет установить границы в которых находится точное число А:
![]() или
или ![]() .
.
Очевидно, что значение абсолютной погрешности приближенного числа не позволяет оценить степень его приближения к точному значению. Для этого используют понятие относительной погрешности приближенного числа, которая вычисляется следующим образом:
 .
.
Из этой формулы видно, что величина ![]() может быть вычислена только при известном значении точного числа А. Если точное значение числа не известно, то используется понятие предельной относительной погрешности
может быть вычислена только при известном значении точного числа А. Если точное значение числа не известно, то используется понятие предельной относительной погрешности
![]() .
.
В практике вычислений величина ![]() определяется по формуле
определяется по формуле
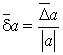 .
.
Полагают, что эта формула применима, если ![]() , В частности, считается нормальным, если
, В частности, считается нормальным, если ![]() или, что то же самое,
или, что то же самое, ![]() . В грубых расчетах допускается
. В грубых расчетах допускается ![]() . Иногда требуется, чтобы
. Иногда требуется, чтобы ![]() .
.
Похожие работы
... нельзя рассматривать как единое целое. Кроме того, необходимо кроме сумматора иметь и вычитатель. В результате этого прямой код не применяется для выполнения операции алгебраического сложения, но применяется для выполнения операций умножения и деления. 1.1.3 Дополнительный код В дополнительном коде операция вычитания заменяется операцией алгебраического сложения. При этом знаковый разряд и ...
... находится в соответствии с данной выше оценкой погрешности и, кроме того, свидетельствует, что формула Симпсона значительно точнее формулы трапеций. Поэтому формулу Симпсона для приближенного вычисления определенных интегралов используют чаще, чем формулу трапеций. Как отмечалось выше, приближенные формулы для вычисления определенного интеграла применяют в тех случаях, когда первообразная ...
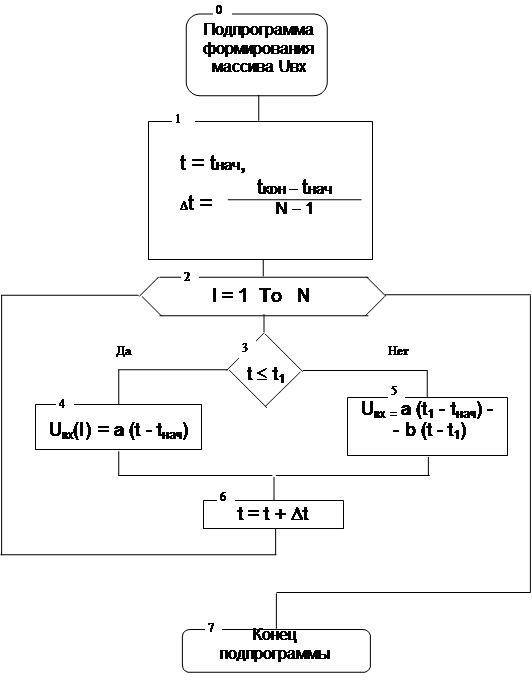
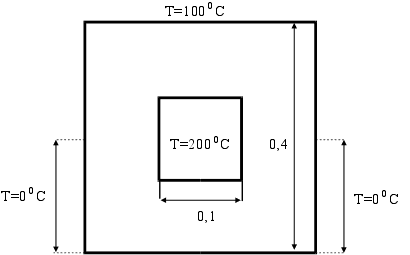
... В данной работе решаются задачи машинного анализа электрических цепей. В курсовом проекте необходимо для заданной электрической цепи по известному входному сигналу UВХ(t) построить выходной сигнал UВЫХ(t) , а затем определить некоторые его характеристики W. Характеристика W вычисляется с погрешностью не более 0.1. Погрешность вычисления величины W зависит от количества расчетных точек N, для ...
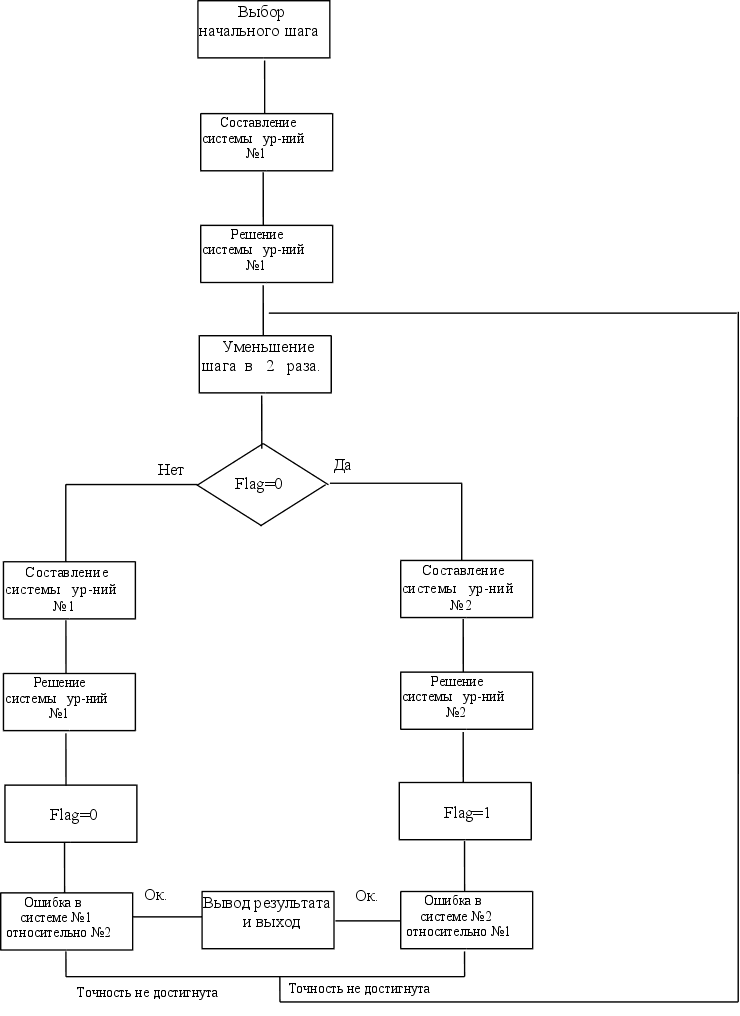
... получают последовательные приближения до тех пор, пока действительная погрешность корней не станет меньше заданной. Различные методы отличаются друг от друга способом вычисления очередного приближения, но во всех методах существуют две главные проблемы: обеспечение сходимости процесса итераций; оценка достигнутой погрешности. Пусть дана линейная система ...

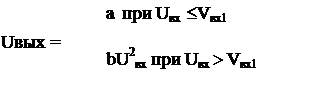


0 комментариев