Навигация
Правила записи приближенных чисел
3. Правила записи приближенных чисел
Для решения инженерных задач часто приходится определять различные числа, как точные, так и приближенные. При этом требуется, чтобы погрешность, возникающая при округлении была бы минимальной.
Пусть некоторое десятичное число представлено его разложением
![]() ,
,
где 10S – единица разряда S, aS – цифра разряда, S – номер разряда.
Все цифры числа от первой слева, неравной нулю, до последней цифры справа называются значащими цифрами.
Например, пусть заданы следующие числа:
a1 = 2.67; a2 = 0.267; a3 = 0.00267; a4 = 0.26700
Тогда для a1, a2, a3 имеем 3 значащие цифры и для a4 - 5 значащих цифр.
Если крайние справа нули не считают значащими, то число записывают в экспоненциальной форме:
![]() ,
,
где m - экспонента, p – порядок числа.
Значащая цифра числа aS называется верной, если абсолютная погрешность этого числа не превосходит половины единицы разряда S, т. е.
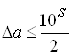 .
.
Если абсолютная погрешность числа не указана, то все его значащие цифры считают верными.
Под округлением числа а будем понимать его замену числом а’, которое имеет меньшее количество значащих цифр, чем исходное число а. Округление должно производиться таким образом, чтобы возникающая ошибка была минимальной.
Для оценки величины ошибки вводят следующие характеристики:
- абсолютная погрешность округления ![]() ;
;
- относительная погрешность округления  .
.
При необходимости могут использоваться их предельные значения:
![]() ;
; ![]() .
.
Если округляется приближенное число, то погрешность полученного числа включает две составляющие:
- погрешность округления;
- погрешность исходного числа.
Округление чисел производится по следующим правилам.
1. Если первая из отбрасываемых цифр меньше 5, то последняя сохраняемая цифра не изменяется.
2. Если первая из отбрасываемых цифр больше 5, то последняя сохраняемая цифра увеличивается на 1.
3. Если первая из отбрасываемых цифр равна 5, и за ней идут не нули, то последняя сохраняемая цифра увеличивается на 1.
4. Если первая из отбрасываемых цифр равна 5 и все значащие цифры, идущие за ней равны нулю, то последняя сохраняемая цифра увеличивается на 1, если она нечетная, и не изменяется, если она четная.
4. Погрешность суммы и разности приближенных чисел
Абсолютная погрешность алгебраической суммы или разности нескольких приближенных чисел не превышает суммы абсолютных погрешностей этих чисел:
![]() ;
;
![]() .
.
Предельная абсолютная погрешность суммы или разности определяется следующим образом:
![]() ;
;
![]() .
.
Оценим относительную погрешность ![]() суммы приближенных чисел. Пусть Х1, Х2 - точные числа одного знака, х1, х2 - их приближения. Тогда
суммы приближенных чисел. Пусть Х1, Х2 - точные числа одного знака, х1, х2 - их приближения. Тогда
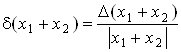 £
£ ![]() (1)
(1)
где ![]() .
.
Предельная относительная погрешность суммы двух чисел вычисляется как
![]() , (2)
, (2)
где ![]() .
.
Формулы (1) и (2) можно обобщить на случай произвольного количества слагаемых:
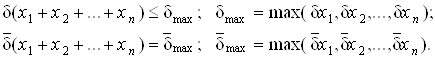
Таким образом, при суммировании чисел одного знака не происходит потери относительной точности, что видно из приведенных соотношений.
Оценка относительной погрешности для разности двух чисел осуществляется по формуле
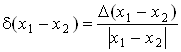 £ ndmax,
£ ndmax,
Где
![]() ;
; 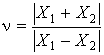 .
.
Формулы для предельных относительных погрешностей имеют вид:
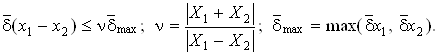
Очевидно, что для разности приближенных чисел относительные погрешности возрастают в n раз, где n > 1. При этом возможна существенная потеря точности, которая происходит в том случае, если числа X1, X2 настолько близки, что их сумма значительно превышает их разность ![]() . Тогда n >> 1, что приводит к полной или почти полной потере точности. Такая ситуация называется катастрофической потерей точности.
. Тогда n >> 1, что приводит к полной или почти полной потере точности. Такая ситуация называется катастрофической потерей точности.
Похожие работы
... нельзя рассматривать как единое целое. Кроме того, необходимо кроме сумматора иметь и вычитатель. В результате этого прямой код не применяется для выполнения операции алгебраического сложения, но применяется для выполнения операций умножения и деления. 1.1.3 Дополнительный код В дополнительном коде операция вычитания заменяется операцией алгебраического сложения. При этом знаковый разряд и ...
... находится в соответствии с данной выше оценкой погрешности и, кроме того, свидетельствует, что формула Симпсона значительно точнее формулы трапеций. Поэтому формулу Симпсона для приближенного вычисления определенных интегралов используют чаще, чем формулу трапеций. Как отмечалось выше, приближенные формулы для вычисления определенного интеграла применяют в тех случаях, когда первообразная ...
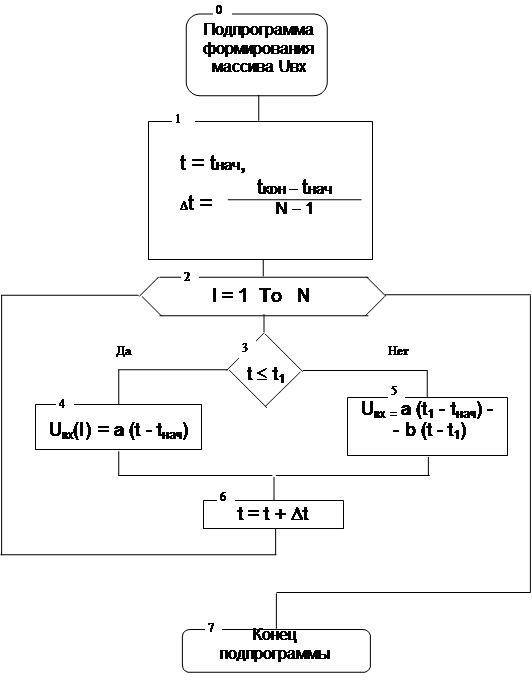
... В данной работе решаются задачи машинного анализа электрических цепей. В курсовом проекте необходимо для заданной электрической цепи по известному входному сигналу UВХ(t) построить выходной сигнал UВЫХ(t) , а затем определить некоторые его характеристики W. Характеристика W вычисляется с погрешностью не более 0.1. Погрешность вычисления величины W зависит от количества расчетных точек N, для ...
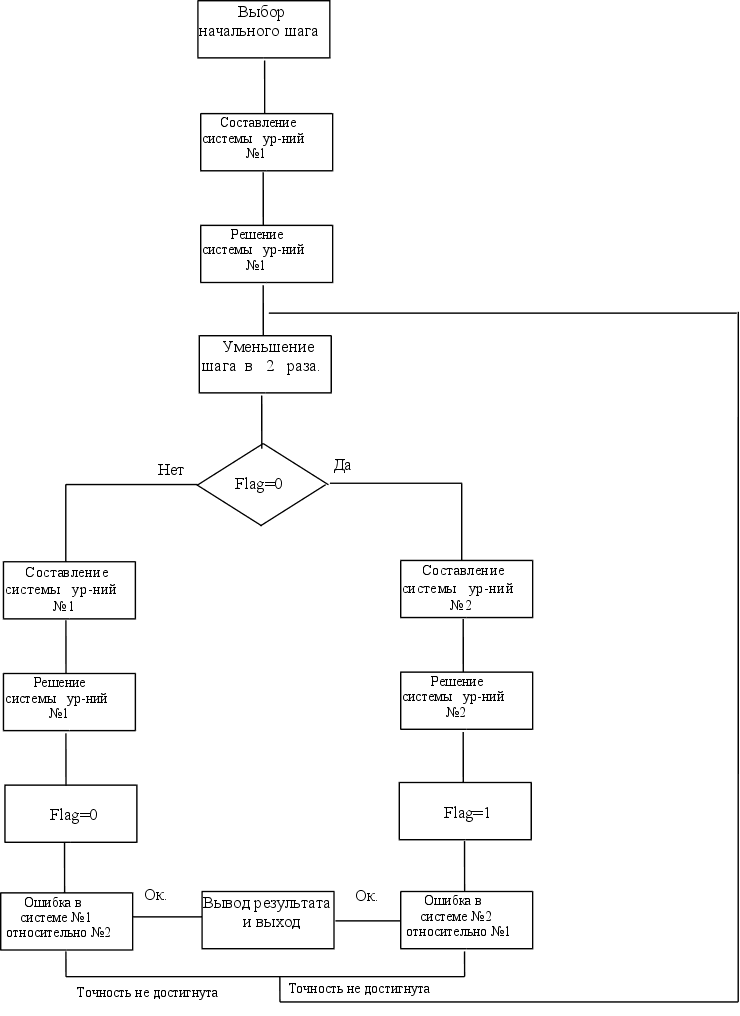
... получают последовательные приближения до тех пор, пока действительная погрешность корней не станет меньше заданной. Различные методы отличаются друг от друга способом вычисления очередного приближения, но во всех методах существуют две главные проблемы: обеспечение сходимости процесса итераций; оценка достигнутой погрешности. Пусть дана линейная система ...

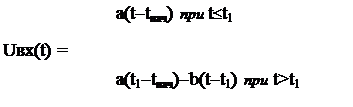
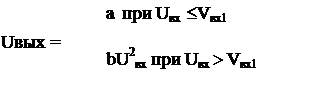


0 комментариев