Структурная схема БИХ-фильтра

2. Структурная схема БИХ-фильтра

Исходя из технического задания необходимо привести структурную схему фильтра в каноническом виде и в виде последовательного соединения звеньев первого и второго порядка.

Каноническая форма реализации рекурсивного фильтра выглядит следующим образом:

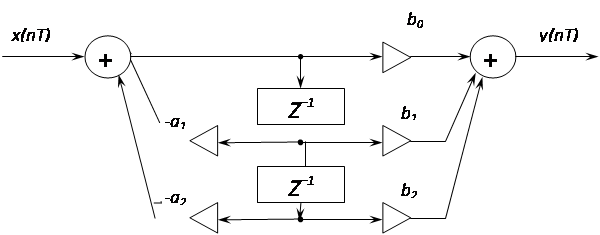
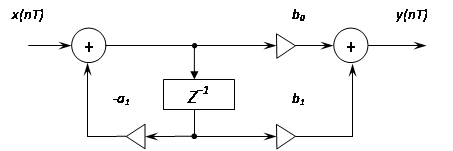
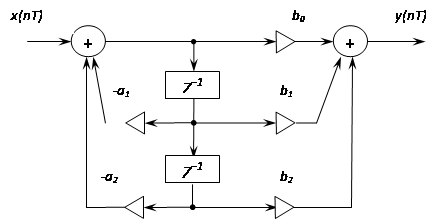
Форма реализации рекурсивного фильтра в виде последовательного соединения звеньев первого и второго порядка представлена на следующем рисунке:

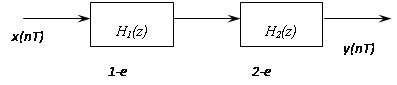
3. Методы расчета БИХ-фильтров и вид целевой функции

Расчет БИХ-фильтров можно вести в частотной и временной областях. При расчете в частотной области используется синтез по аналоговому и цифровому прототипам. Численные методы расчета разработаны для применения в частотной и временной областях.

Синтез по аналоговому прототипу основан на преобразовании p-плоскости в z-плоскость, а характеристик и параметров аналоговых фильтров - в соответствующие характеристики и параметры цифровых фильтров. Передаточная функция аналогового фильтра на p-плоскости в общем виде может быть записана так:

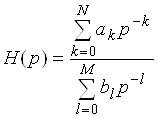. (1)

Для перехода к функции  и разностному уравнению ЦФ существуют следующие четыре метода.

Метод 1. Отображение дифференциалов. Это наиболее простой метод, сущность которого заключается в замене дифференциалов на конечные разности. В операторном уравнении (1), если дифференциалы заменяются прямыми разностями, то

или  ,

а если обратными, то

 или .

Недостатком метода является неполное соответствие частотно-избирательных свойств ЦФ свойствам аналогового прототипа. Кроме того, при использовании прямых разностей устойчивый аналоговый фильтр - прототип отображается в неустойчивый ЦФ. Поэтому, несмотря на простоту, применять этот метод не рекомендуется.

Метод 2. Инвариантное преобразование импульсной характеристики (стандартное Z-преобразование). Сущность метода заключается в расчете импульсной характеристики (ИХ) ЦФ по аналоговому прототипу и вычислении системной (передаточной) функции ЦФ.

Достоинством данного метода является подобие импульсных характеристик ЦФ и аналогового прототипа; простота. Недостатком же является наличие эффекта наложения частотных характеристик ЦФ, если полоса пропускания аналогового прототипа превышает . Поэтому точность расчетов ЦФ по данному методу тем выше, чем меньше отношение , где  - верхняя частота полосы пропускания ЦФ;  - частота дискретизации.

Метод 3. Согласованное Z-преобразование. Полюсы и нули аналогового прототипа на p-плоскости отображаются в полюсы и нули ЦФ на z-плоскости по правилу:

.

Для реализации этого метода передаточную функцию аналогового прототипа представляют в виде произведения сомножителей

,

где ,  - действительные или комплексно-сопряженные коэффициенты. Метод согласованного Z-преобразования не применим, если передаточная функция аналогового прототипа имеет только полюсы (нули расположены в бесконечности). Для устранения этого недостатка при расчетах фильтров с нулями в бесконечности рекомендуется вводить полюс того же порядка, что и нуль, в точке .

Метод 4. Билинейное (дробно-линейное) Z-преобразование. При отображении p-плоскости в z-плоскость вся мнимая ось ,  отображается в единичную окружность. Для этого необходимо выбирать нелинейную монотонную функцию частоты. Эта функция должна изменяться в пределах от  до  на оси частот дискретизации при изменении  от  до . В качестве такой функции комплексных частот можно выбрать гиперболический тангенс

или , (2)

которому при  соответствует обычный тангенс

.

Гиперболический тангенс в выражении (2) можно представить следующим образом:

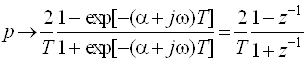. (3)

Таким образом, комплексная плоскость p преобразуется в комплексную z-плоскость заменой переменных (3).

С помощью билинейных Z-преобразований можно от аналогового ФНЧ - прототипа перейти к ЦФ нижних частот (НЧ), верхних частот (ВЧ), полосовому, режекторному, гребенчатому и др.

Билинейное Z-преобразование обладает следующими достоинствами: во-первых, физически реализуемый и устойчивый аналоговый фильтр отображается в физически реализуемый и устойчивый ЦФ: во-вторых, отсутствуют проблемы, связанные с наложениями: в-третьих, нелинейность шкалы частот ЦФ, преобразованного из прототипа, можно учесть для широкого класса фильтров.

Недостатком этого метода является не совпадение импульсной и фазовой характеристик рассчитанного прототипа, поэтому необходимо вводить корректоры и усложнять конструкцию ЦФ. Тем не менее метод билинейного Z-преобразования является самым распространенным аналитическим методом расчета ЦФ.

Для синтеза БИХ ЦФ по цифровому прототипу используются преобразования ЦФ НЧ с безразмерной частотой среза  в ЦФ НЧ с другой частотой среза, ЦФ ВЧ, полосовой, режекторный или гребенчатый фильтры. Методика расчета по цифровому прототипу проще, чем методика расчета по аналоговому прототипу, так как в ней отсутствует этап перехода от аналогового фильтра - прототипа к ЦФ.

Применение методов оптимизации для расчета БИХ-фильтров.

В последние годы широкое распространение получил другой класс методов расчета БИХ-фильтров, называемых методами оптимизации. Отличительной чертой этих методов является то, что система уравнений, составленная относительно коэффициентов фильтра, не может быть решена в явной форме. Поэтому для нахождения коэффициентов приходится использовать численные методы оптимизации, минимизирующие, согласно выбранному критерию, некоторую ошибку.

В качестве такого критерия используется критерий минимума среднеквадратической ошибки. При этом целевая функция задачи имеет вид

,

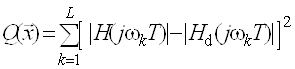где - ()-мерный вектор искомых коэффициентов,  - получаемая амплитудная характеристика фильтра,  - заданная амплитудная характеристика фильтра, ,  - дискретный ряд частот, на которых вычисляются отклонения получаемой и заданной характеристик фильтра.

Минимизация функции  сводится к нахождению оптимального значения параметрического вектора весовых коэффициентов фильтра . Так как функция  является нелинейной, для ее минимизации необходимо использовать эффективные методы оптимизации.

При использовании методов оптимизации учитывается поведение только амплитудной характеристики, поэтому некоторые полюсы или нули после завершения итераций могут оказаться за пределами единичного круга. В этом случае можно прежде всего заменить полюс с полярными координатами , оказавшийся вне единичного круга, на полюс с координатами , находящийся внутри единичного круга. Амплитудная характеристика фильтра при такой замене остается неизменной, так как полюс заменяется своим зеркальным отображением. После того, как все полюсы оказываются внутри единичного круга, появляется возможность с помощью дополнительного анализа еще больше оптимизировать квадрат ошибки. Такая ситуация возникает достаточно часто, и в этих случаях оптимизация должна производиться двумя этапами:

1.  Использование программы оптимизации для минимизации функции  без каких-либо ограничений на расположение нулей и полюсов.

2.  После завершения итераций инвертирование всех полюсов и нулей, оказавшихся вне единичного круга. После этого продолжение оптимизации для нахождения нового минимума .