Навигация
Процесс создания математической модели объекта
Содержание
1. Введение
2. Задание на курсовую работу
1.Обработка исходных данных методом площадей
2.Частотные характеристики
3.По заданному закону регулирования найти математическую модель ЗСАУ
4.Определение устойчивости ЗСАУ
5.Нахождение переходной характеристики ЗСАУ и основных ПКР
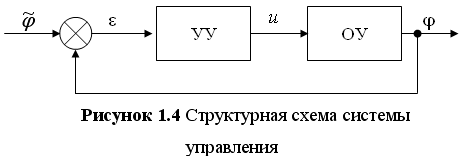
6.Функциональная схема
7.Вывод
3. Заключение
4. Список литературы
5. Приложение
Введение
Управление состоянием сложных систем всегда связано с необходимостью получения информации об этом состоянии и его целенаправленных и хаотических изменениях.
В данной работе было предложено смоделировать простую систему регулирования давления. Данные системы используются во многих отраслях промышленности, поэтому исследования их классических моделей являются довольно оправданными. Также, зачастую, проектировщики сталкиваются с тем, что в системе уже внедрены некоторые функции контроля, но их адекватность и качество работы не всегда легко определить. Поэтому было предложено определить объекты регулирования в системах по имеющимся выходным характеристикам, используя метод площадей для определения их передаточных функций, а также внедрение новых регуляторов, с заданными коэффициентами, с проверкой системы на устойчивость.
Подобные исследования в настоящее время проводятся часто, в связи с тем, что утрачивается та или иная документация по системам, и проектировщикам для модернизации необходимо знать, с чем они имеют дело изначально.
Задание на курсовую работу.
1. По экспериментальным данным найти математическую модель объекта (системы) методом площадей в виде звена 2-го или 3-го порядка. Оценить точность аппроксимации.
2. Найти и построить частотные характеристики объекта (АЧХ, ФЧХ, АФЧХ) и провести подробный анализ этих характеристик.
3. По заданному закону регулирования найти математическую модель ЗСАУ.
4. Определить устойчивость ЗСАУ по одному из критериев. Если система неустойчива, то добиться ее устойчивости.
5. Найти переходную функцию ЗСАУ и построить ее. Найти по кривой основные ПКР.
6. Привести структурную схему САУ в соответствии с требованиями ГОСТ.
7. Дать выводы по работе.
| t | 0 | 0.25 | 0.3 | 0.35 | 0,5 | 0,75 | 1 | 1.25 | 1,5 | 1.75 | 2 | 2.25 | 2,5 |
| s | 0 | 0.05 | 0.07 | 0.09 | 0.11 | 0.13 | 0.16 | 0.19 | 0.21 | 0.25 | 0.29 | 0.35 | 0.4 |
| t | 2.7 | 3 | 3,2 | 4,25 | 4.5 | 4.75 | 5 | 5,25 | 5.5 | 5.75 | 6 |
| s | 0.45 | 0.5 | 0.55 | 0.6 | 0.7 | 0.75 | 0.8 | 0.85 | 0.9 | 0.95 | 1 |
Объект регулирования АПЗ-2
Похожие работы
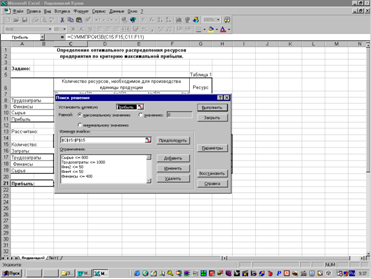
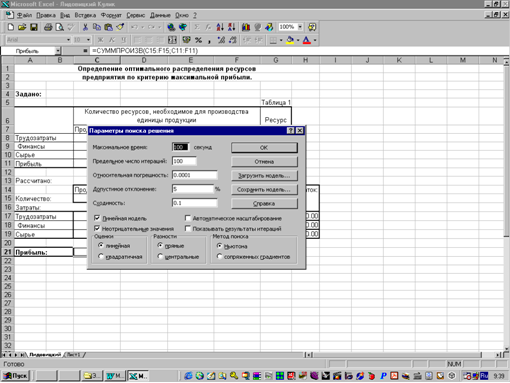
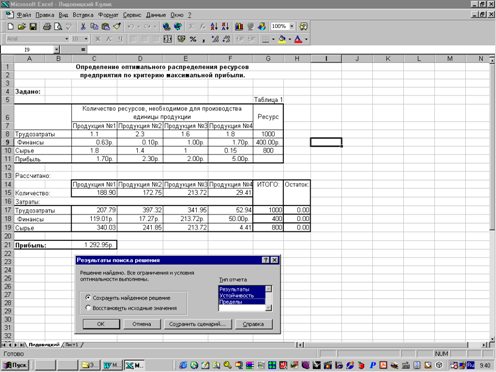
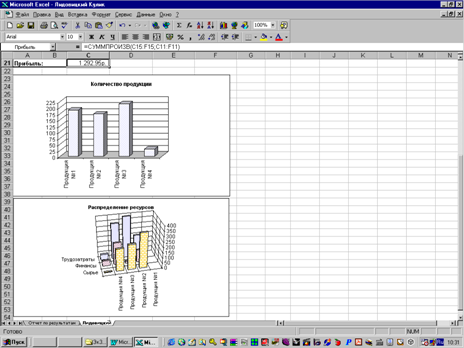
... полностью. Структура найденного решения наиболее сильно зависит от реализации единицы продукции №1 и №3, а также от уменьшения или увеличения всех имеющихся ресурсов. Часть № 2 "Расчет экономико-математической модели межотраслевого баланса Теоретические положения. Балансовый метод - метод взаимного сопоставления финансовых, материальных и трудовых ресурсов и потребностям в них. Балансовая ...
... параметрами, показателями объекта именно в то время. Дискретные модели отображают состояние объекта управления в отдельные, фиксированные моменты времени. Имитационными называют экономико-математические модели, используемые с целью имитации управляемых экономических объектов и процессов с применением средств информационной и вычислительной техники. По типу математического аппарата, применяемого в ...
... своевременное распределение средств на развитие. Данными вопросами я и занимаюсь в настоящей дипломной работе. 4. Математическое моделирование Интернет - услуг 4.1 Математическое моделирование dial-up подключений Сначала рассмотрим моделирование услуги предоставления доступа в Интернет по dial-up, так как данная услуга является показателем потенциальных абонентов для монопольной услуги ...
... проектирования. Целью проекта является создание программного продукта (ПП), основанного на математическом пакете MatLab, реализующего математическую модель системы управления, построенной на основе оптимального закона, для системы слежения РЛС. Данный проект можно отнести к научно-исследовательской работе, которая принадлежит к типу прикладных, направленных на решение научных проблем с целью ...

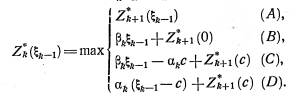
0 комментариев