Дипломна робота
Дослідження проблеми тригонометричних рівнянь
ВВЕДЕННЯ
У стародавності тригонометрія виникла у зв'язку з потребами астрономії, будівельної справи, тобто носила чисто геометричний характер і представляла головним чином <<вирахування хорд>>. Згодом у неї почали вкраплятися деякі аналітичні моменти. У першій половині 18-го століття відбувся різкий перелом, після чого тригонометрія прийняла новий напрямок і змістилася убік математичного аналізу. Саме в цей час тригонометричні залежності стали розглядатися як функції.
Тригонометричні рівняння одна із самих складних тем у шкільному курсі математики. Тригонометричні рівняння виникають при рішенні задач по планіметрії, стереометрії, астрономії, фізики й в інших областях. Тригонометричні рівняння й нерівності рік у рік зустрічаються серед завдань централізованого тестування.
Найважливіша відмінність тригонометричних рівнянь від алгебраїчних полягає в тому, що в алгебраїчних рівняннях кінцеве число корінь, а в тригонометричних нескінченне, що сильно ускладнює відбір корінь. Ще одною специфікою тригонометричних рівнянь є не одиничність форми запису відповіді.
Дана дипломна робота присвячена методам рішення тригонометричних рівнянь і нерівностей.
Дипломна робота складається з 6 розділів.
У першому розділі наведені основні теоретичні відомості: визначення й властивості тригонометричних і зворотних тригонометричних функцій; таблиця значень тригонометричних функцій для деяких аргументів; вираження тригонометричних функцій через інші тригонометричні функції, що дуже важливо для перетворення тригонометричних виражень, що особливо містять зворотні тригонометричні функції; крім основних тригонометричних формул, добре відомих зі шкільного курсу, наведені формули вираження, що спрощують, утримуючі зворотні тригонометричні функції.
У другому розділі викладені основні методи рішення тригонометричних рівнянь. Розглянуто рішення елементарних тригонометричних рівнянь, метод розкладання на множники, методи відомості тригонометричних рівнянь до алгебраїчного. Через те, що рішення тригонометричних рівнянь можна записати декількома способами, і вид цих рішень не дозволяє відразу встановити, чи є ці рішення однаковими або різними, що може <<спантеличити>> при рішенні тестів, розглянута загальна схема рішення тригонометричних рівнянь і докладно розглянуте перетворення груп загальних рішень тригонометричних рівнянь.
У третьому розділі розглядаються нестандартні тригонометричні рівняння, рішення яких засноване на функціональному підході.
У четвертому розділі розглядаються тригонометричні нерівності. Докладно розглянуті методи рішення елементарних тригонометричних нерівностей, як на одиничній окружності, так і графічним методом. Описано процес рішення неелементарних тригонометричних нерівностей через елементарні нерівності й уже добре відомий школярам метод інтервалів.
У п'ятому розділі представлені найбільш складні завдання: коли необхідно не тільки вирішити тригонометричне рівняння, але й зі знайдених корінь відібрати корінь, що задовольняють якій-небудь умові. У даному розділі наведені рішення типових завдань на відбір корінь. Наведено необхідні теоретичних відомості для відбору корінь: розбивка множини цілих чисел на непересічні підмножини, рішення рівнянь у цілих числах (діафантових).
У шостому розділі представлені задачі для самостійного рішення, оформлені у вигляді тесту. В 20 завданнях тесту наведені найбільш складні завдання, які можуть зустрітися на централізованому тестуванні.
ОСНОВНІ МЕТОДИ РІШЕННЯ ТРИГОНОМЕТРИЧНИХ РІВНЯНЬ
Елементарні тригонометричні рівняння
Елементарні тригонометричні рівняння - це рівняння виду
![]()
де ![]() - одна із тригонометричних функцій
- одна із тригонометричних функцій
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Елементарні тригонометричні рівняння мають нескінченно багато корінь. Наприклад, рівнянню
![]()
задовольняють наступні значення
![]() ,
, ![]() ,
, ![]() ,
, ![]()
і т.д. Загальна формула по який перебувають всі коріння рівняння
![]() , де
, де ![]() , така:
, така:
![]()
Тут ![]() може приймати будь-які цілі значення, кожному з них відповідає певний корінь рівняння; у цій формулі (так само як і в інших формулах, по яких вирішуються елементарні тригонометричні рівняння)
може приймати будь-які цілі значення, кожному з них відповідає певний корінь рівняння; у цій формулі (так само як і в інших формулах, по яких вирішуються елементарні тригонометричні рівняння) ![]() називають параметром. Записують звичайно
називають параметром. Записують звичайно ![]() , підкреслюючи тим самим, що параметр
, підкреслюючи тим самим, що параметр ![]() приймати будь-які цілі значення.
приймати будь-які цілі значення.
Рішення рівняння
![]()
де ![]() , перебувають по формулі
, перебувають по формулі
![]()
Рівняння ![]() вирішується застосовуючи формулу
вирішується застосовуючи формулу
![]()
а рівняння ![]() -по формулі
-по формулі
![]()
Особливо відзначимо деякі окремі випадки елементарних тригонометричних рівнянь, коли рішення може бути записане без застосування загальних формул:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
При рішенні тригонометричних рівнянь важливу роль грає період тригонометричних функцій. Тому приведемо дві корисні теореми:
Теорема Якщо ![]() --- основний період функції
--- основний період функції ![]() , то число
, то число ![]() є основним періодом функції
є основним періодом функції ![]() .
.
Періоди функцій ![]() і
і ![]() називаються порівнянними, якщо існують натуральні числа
називаються порівнянними, якщо існують натуральні числа ![]() й
й ![]() , що
, що ![]() .
.
Теорема Якщо періодичні функції ![]() й
й ![]() , мають порівнянні
, мають порівнянні ![]() й
й ![]() , те вони мають загальний період
, те вони мають загальний період
![]()
що є періодом функцій
![]() ,
, ![]() ,
, ![]()
У теоремі говориться про те, що ![]() є періодом функції
є періодом функції
![]() ,
, ![]() ,
, ![]()
і не обов'язково є основним періодом. Наприклад, основний період функцій
![]() і
і ![]() -
- ![]()
а основний період їхнього добутку - ![]() .
.
Введення допоміжного аргументу
Стандартним шляхом перетворення виражень виду
![]() є
є
наступний прийом: нехай ![]() - кут, що задається рівностями
- кут, що задається рівностями
![]()
![]()
Для будь-яких ![]() і
і ![]() такий кут існує. У такий спосіб
такий кут існує. У такий спосіб
![]()
Якщо
![]() ,
, ![]() або
або ![]() ,
, ![]() ,
, ![]() в інших випадках
в інших випадках ![]()
Схема рішення тригонометричних рівнянь
Основна схема, який ми будемо керуватися при рішенні тригонометричних рівнянь наступна:
рішення заданого рівняння зводиться до рішення елементарних рівнянь. Засоби рішення -і- перетворення, розкладання на множники, заміна невідомих. Провідний принцип -і- не втрачати корінь. Це означає, що при переході до наступного рівняння (рівнянням) ми не побоюємося появи зайвих (сторонніх) корнів, а піклуємося лише про те, щоб кожне наступне рівняння нашої "ланцюжка" (або сукупність рівнянь у випадку розгалуження) було наслідком попередні. Одним з можливих методів відбору корнів є перевірка. Відразу помітимо, що у випадку тригонометричних рівнянь труднощі, пов'язані з відбором корнів, з перевіркою, як правило, різко зростають у порівнянні з алгебраїчними рівняннями. Адже перевіряти доводиться серії, що складаються з нескінченного числа членів.
Особливо варто сказати про заміну невідомих при рішенні тригонометричних рівнянь. У більшості випадків після потрібної заміни виходить алгебраїчне рівняння. Більше того, не так уже й рідкі рівняння, які, хоча і є тригонометричними по зовнішньому вигляді, по суті такими не є, оскільки вже після першого кроку -і- заміни змінних -і- перетворюються в алгебраїчні, а повернення до тригонометрії відбувається лише на етапі рішення елементарних тригонометричних рівнянь.
Ще раз нагадаємо: заміну невідомого варто робити з першою нагодою, що вийшла після заміни рівняння необхідно вирішити до кінця, включаючи етап відбору корнів, а потім вернеться до первісного невідомого.
Одна з особливостей тригонометричних рівнянь полягає в тім, що відповідь у багатьох випадках може бути записаний різними способами. Навіть для рішення рівняння ![]() відповідь може бути записаний у такий спосіб:
відповідь може бути записаний у такий спосіб:
1) у вигляді двох серій
![]() ,
, ![]() ,
, ![]()
2) у стандартній формі що представляє собою об'єднання зазначених вище серій
![]() ,
, ![]()
3) оскільки
![]()
те відповідь можна записати у вигляд
![]() ,
, ![]()
(Надалі наявність параметра ![]() ,
, ![]() ,
, ![]() або
або ![]() в записі відповіді автоматично означає, що цей параметр приймає всілякі цілочисленні значення. Виключення будуть обмовлятися.)
в записі відповіді автоматично означає, що цей параметр приймає всілякі цілочисленні значення. Виключення будуть обмовлятися.)
Очевидно, що трьома перерахованими випадками не вичерпуються всі можливості для запису відповіді розглянутого рівняння (їх нескінченно багато).
Наприклад, при ![]() справедливо рівність
справедливо рівність
![]()
Отже, у двох перших випадках, якщо ![]() , ми можемо замінити
, ми можемо замінити
![]() на
на ![]()
Звичайно відповідь записується на підставі пункту 2. Корисно запам'ятати наступну рекомендацію: якщо на рішенні рівняння ![]() робота не закінчується, необхідно ще провести дослідження, відбір корнів, те найбільш зручна форма запису, зазначена в пункті 1. (Аналогічну рекомендацію варто дати й для рівняння
робота не закінчується, необхідно ще провести дослідження, відбір корнів, те найбільш зручна форма запису, зазначена в пункті 1. (Аналогічну рекомендацію варто дати й для рівняння ![]() .)
.)
Розглянемо приклад.
Приклад Вирішити рівняння
![]()
Рішення. Найбільш очевидним є наступний шлях. Дане рівняння розпадається на два
![]() і
і ![]()
Вирішуючи кожне з них і поєднуючи отримані відповіді, знайдемо
![]()
Інший шлях. Оскільки
![]() ,
,
те, заміняючи ![]() й
й ![]() по формулах зниження ступеня. Після невеликих перетворень одержимо
по формулах зниження ступеня. Після невеликих перетворень одержимо
![]() Звідки
Звідки ![]()
На перший погляд ніяких особливих переваг у другої формули в порівнянні з першої немає. Однак, якщо візьмемо, наприклад,
![]()
те виявиться, що
![]()
тобто рівняння
![]()
має рішення
![]()
у той час як перший спосіб нас приводить до відповіді
![]()
Побачити" і довести рівність
![]() не так просто.
не так просто.
Відповідь. ![]()
Перетворення й об'єднання груп загальних рішень тригонометричних рівнянь
Будемо розглядати арифметичну прогресію, що нескінченно простирається в обидва боки. Члени цієї прогресії можна розбити на дві групи членів, що розташовуються вправо й уліво від деякого члена, називаного центральним або нульовим членом прогресії.
Фіксуючи один зі членів нескінченної прогресії нульовим номером, ми повинні будемо вести подвійну нумерацію для всіх членів, що залишилися: позитивну для членів, розташованих вправо, і негативну для членів, розташованих уліво від нульового.
У загальному випадку, якщо різниця прогресії ![]() , нульовий член
, нульовий член ![]() , формула для кожного (
, формула для кожного (![]() -го) члена нескінченної арифметичної прогресії представляє вид:
-го) члена нескінченної арифметичної прогресії представляє вид:
![]()
Перетворення формули для будь-якого члена нескінченної арифметичної прогресії
1. Якщо до нульового члена ![]() додати або відняти різниця прогресії
додати або відняти різниця прогресії ![]() , то від цього прогресія не зміниться, а тільки переміститься нульовий член, тобто зміниться нумерація членів.
, то від цього прогресія не зміниться, а тільки переміститься нульовий член, тобто зміниться нумерація членів.
2. Якщо коефіцієнт при змінній величині ![]() помножити на
помножити на ![]() , то від цього відбудеться лише перестановка правої й лівої груп членів.
, то від цього відбудеться лише перестановка правої й лівої груп членів.
3. Якщо ![]() послідовних членів нескінченної прогресії
послідовних членів нескінченної прогресії
![]()
наприклад
![]() ,
, ![]() ,
, ![]() , ...,
, ..., ![]()
зробити центральними членами ![]() прогресій з однаковою різницею, рівної
прогресій з однаковою різницею, рівної ![]() :
:
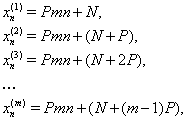
те прогресія (??) й ряд прогресій (??) виражають собою ті самі числа.
Приклад Ряд
![]()
може бути замінений наступними трьома рядами
![]() ,
, ![]() ,
, ![]()
4. Якщо ![]() нескінченних прогресій з однаковою різницею
нескінченних прогресій з однаковою різницею ![]() мають центральними членами числа, що утворять арифметичну прогресію з різницею
мають центральними членами числа, що утворять арифметичну прогресію з різницею ![]() , то ці
, то ці ![]() рядів можуть бути замінені одною прогресією з різницею
рядів можуть бути замінені одною прогресією з різницею ![]() , і із центральним членом, рівним кожному із центральних членів даних прогресій, тобто якщо
, і із центральним членом, рівним кожному із центральних членів даних прогресій, тобто якщо
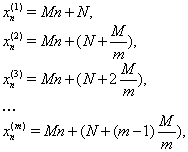
те ці ![]() прогресій поєднуються в одну
прогресій поєднуються в одну
![]()
Приклад
![]() ,
, ![]() ,
, ![]() ,
, ![]()
обидві поєднуються в одну групу
![]() , тому що
, тому що ![]()
Для перетворення груп, що мають загальні рішення, у групи, загальних рішень не дані групи, що мають, розкладають на групи із загальним періодом, а потім об'єднати групи, що вийшли, виключивши повторювані.
Розкладання на множники
Метод розкладання полягає в наступному: якщо
![]()
те всяке рішення рівняння
![]()
є рішення сукупності рівнянь
![]() (??)
(??)
Зворотне твердження, загалом кажучи невірно: не всяке рішення сукупності є рішенням рівняння. Це пояснюється тим, що рішення окремих рівнянь (??) можуть не входити в область визначення функції ![]() .
.
Приклад Вирішити рівняння
![]()
Рішення. Використовуючи основну тригонометричну тотожність, рівняння представимо у вигляді
![]()
Відповідь.![]() ;
; ![]()
Перетворення суми тригонометричних функцій у добуток
Приклад Вирішити рівняння
![]()
Рішення. Застосуємо формулу (??), одержимо рівносильне рівняння
![]()
Відповідь. ![]()
Приклад Вирішити рівняння
![]()
Рішення. У цьому випадку, перш ніж застосовувати формули суми тригонометричних функцій, варто використовувати формулу приведення
![]()
У підсумку одержимо рівносильне рівняння
![]()
Відповідь. ![]() ,
, ![]() .
.
Рішення рівнянь добутку тригонометричних функцій у суму
При рішенні ряду рівнянь застосовуються формули.
Приклад Вирішити рівняння
![]()
Рішення. Застосувавши формулу (??), одержимо рівносильне рівняння:
![]()
Відповідь. ![]() ,
, ![]()
Приклад Вирішити рівняння
![]() .
.
Рішення. Застосувавши формулу (??), одержимо рівносильне рівняння:
![]() .
.
Відповідь. ![]()
Рішення рівнянь із застосуванням формул зниження ступеня
При рішенні широкого кола тригонометричних рівнянь ключову роль грають формули.
Приклад Вирішити рівнянн
![]()
Рішення. Застосовуючи формулу, одержимо рівносильне рівняння.
![]()
![]()
![]()
![]() .
.
Відповідь. ![]() ;
; ![]() .
.
Рішення рівнянь із формул потрійного аргументу
Приклад Вирішити рівняння
![]()
Рішення. Застосуємо формулу (??), одержимо рівняння
![]()
Відповідь. ![]() ;
; ![]() .
.
Приклад Вирішити рівняння
![]() .
.
Рішення
Застосуємо формули зниження ступеня одержимо
![]()
Застосовуючи (??) одержуємо
![]()
Відповідь. ![]() ;
; ![]()
Рівність однойменних тригонометричних функцій
![]()
![]()
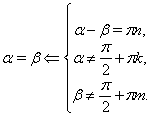
Приклад Вирішити рівняння
![]() .
.
Рішення
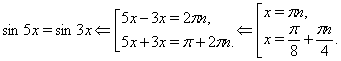
Відповідь. ![]() ,
, ![]() .
.
Приклад Вирішити рівняння
![]()
Рішення. Перетворимо рівняння
![]()
Відповідь. ![]() .
.
Приклад Відомо, що ![]() й
й ![]() задовольняють рівнянню
задовольняють рівнянню
![]()
Знайти суму ![]() .
.
Рішення. З рівняння треба, що
![]()
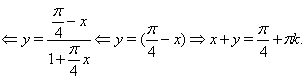
Відповідь. ![]()
Помноження на деяку тригонометричну функцію
Розглянемо суми виду
![]()
![]()
Дані суми можна перетворити в добуток, до множив і розділивши їх на
![]() , тоді одержимо
, тоді одержимо
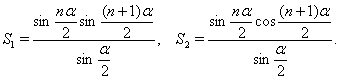
Зазначений прийом може бути використаний при рішенні деяких тригонометричних рівнянь, однак варто мати на увазі, що в результаті можлива поява сторонніх корінь. Приведемо узагальнення даних формул:
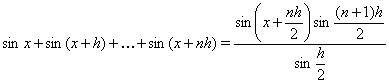
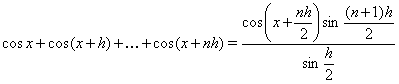
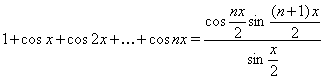
Приклад Вирішити рівняння
![]()
Рішення. Видно, що множина ![]() є рішенням вихідного рівняння. Тому множення лівої й правої частини рівняння на
є рішенням вихідного рівняння. Тому множення лівої й правої частини рівняння на ![]() не приведе до появи зайвих корінь.
не приведе до появи зайвих корінь.
Маємо ![]()
Відповідь. ![]() ;
; ![]()
Приклад Вирішити рівняння
![]()
Рішення. До множимо ліву й праву частини рівняння на
![]()
й застосувавши формули перетворення добутку тригонометричних функцій у суму, отримаємо
![]()
Це рівняння рівносильне сукупності двох рівнянь
![]() і
і ![]() , звідки
, звідки ![]() й
й ![]()
Тому що корінь рівняння
![]()
не є коріннями рівняння, то з отриманих множин рішень варто виключити
![]()
Значить у множині
![]() потрібно виключити
потрібно виключити ![]() .
.
Відповідь. ![]() і
і ![]() ,
, ![]() .
.
Приклад Вирішити рівняння
![]()
Рішення. Перетворимо вираження
![]()
![]()
Рівняння запишеться у вигляді
![]()
Приймаючи ![]() , одержуємо
, одержуємо ![]() .
. ![]() ,
, ![]()
Отже
Відповідь. ![]()
Відомість тригонометричних рівнянь до алгебраїчних
Зведених до квадратних
Якщо рівняння має вигляд
![]()
те заміна ![]() приводить його до квадратного, оскільки
приводить його до квадратного, оскільки
![]() ((??) ) і (??).
((??) ) і (??).
Якщо замість доданка ![]() буде
буде![]() , то потрібна заміна буде
, то потрібна заміна буде
![]()
Рівняння
![]()
зводиться до квадратного рівняння
![]()
поданням ![]() як
як ![]() . Легко перевірити, що
. Легко перевірити, що ![]() при яких
при яких ![]() , не є коріннями рівняння, і, зробивши заміну
, не є коріннями рівняння, і, зробивши заміну ![]() , рівняння зводиться до квадратного.
, рівняння зводиться до квадратного.
Приклад Вирішити рівняння
![]()
Рішення. Перенесемо ![]() в ліву частину, замінимо її на
в ліву частину, замінимо її на
![]() ,
, ![]() і
і ![]() виразимо через
виразимо через ![]() і
і ![]()
Після спрощень одержимо
![]()
Розділимо по членне на ![]() , зробимо заміну
, зробимо заміну ![]() :
:
![]()
Вертаючись до ![]() , знайдемо
, знайдемо
![]()
Рівняння, однорідні відносно ![]() ,
, ![]()
Розглянемо рівняння виду
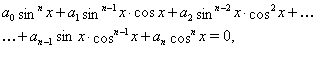 (8)
(8)
де ![]() ,
, ![]() ,
, ![]() , ...,
, ..., ![]() ,
, ![]() --- дійсні числа. У кожному складати^ся лівої частини рівняння (??) ступеня одночленів рівні
--- дійсні числа. У кожному складати^ся лівої частини рівняння (??) ступеня одночленів рівні ![]() , тобто сума ступенів синуса й косинуса та сама й дорівнює
, тобто сума ступенів синуса й косинуса та сама й дорівнює ![]() . Таке рівняння називається однорідним відносно
. Таке рівняння називається однорідним відносно ![]() й
й ![]() , а число
, а число ![]() називається показником однорідності.
називається показником однорідності.
Ясно, що якщо ![]() , те рівняння прийме вид:
, те рівняння прийме вид:
![]()
рішеннями якого є значення ![]() , при яких
, при яких ![]() , тобто числа
, тобто числа ![]() ,
, ![]() . Друге рівняння, записане в дужках також є однорідним, але ступеня на 1 нижче.
. Друге рівняння, записане в дужках також є однорідним, але ступеня на 1 нижче.
Якщо ж ![]() , то ці числа не є коріннями рівняння (??).
, то ці числа не є коріннями рівняння (??).
При ![]() одержимо:
одержимо: ![]() ,
, ![]() і ліва частина рівняння (1) приймає значення
і ліва частина рівняння (1) приймає значення ![]() .
.
Отже, при ![]() ,
, ![]() і
і ![]() , тому можна розділити обидві частини рівняння на
, тому можна розділити обидві частини рівняння на ![]() . У результаті одержуємо рівняння:
. У результаті одержуємо рівняння:
![]()
яке, підстановкою ![]() легко зводиться до алгебраїчного:
легко зводиться до алгебраїчного:
![]()
Однорідні рівняння з показником однорідності 1. При ![]() маємо рівняння
маємо рівняння ![]() .
.
Якщо ![]() , то це рівняння рівносильне рівнянню
, то це рівняння рівносильне рівнянню
![]() ,
, ![]() , звідки
, звідки ![]() ,
, ![]()
Приклад Вирішите рівняння
![]()
Рішення. Це рівняння однорідне першого ступеня ![]() . Розділимо обидві його частини на
. Розділимо обидві його частини на ![]() одержимо:
одержимо:
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Відповідь. ![]() .
.
Приклад При ![]() одержимо однорідне рівняння виду
одержимо однорідне рівняння виду
![]()
Рішення
Якщо ![]() , тоді розділимо обидві частини рівняння на
, тоді розділимо обидві частини рівняння на ![]() , одержимо рівняння
, одержимо рівняння ![]() , що підстановкою
, що підстановкою ![]() легко приводиться до квадратного:
легко приводиться до квадратного: ![]() . Якщо
. Якщо ![]() , то рівняння має дійсні коріння
, то рівняння має дійсні коріння ![]() ,
, ![]() . Вихідне рівняння буде мати дві групи рішень:
. Вихідне рівняння буде мати дві групи рішень: ![]() ,
, ![]()
![]() ,
, ![]() .
.
Якщо ![]() , то рівняння не має рішень.
, то рівняння не має рішень.
Приклад Вирішите рівняння ![]() .
.
Рішення
Це рівняння однорідне другого ступеня. Розділимо обидві честі рівняння на ![]() , одержимо
, одержимо![]()
Нехай ![]() , тоді
, тоді
![]() ,
, ![]() ,
, ![]() .
. ![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
, ![]()
Відповідь. ![]()
До рівняння виду (??) зводиться рівняння
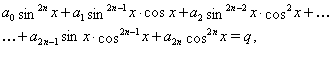
Для цього досить скористатися тотожністю
![]()
Зокрема, рівняння
![]()
зводиться до однорідного, якщо замінити ![]() на
на
![]()
тоді одержимо рівносильне рівняння
![]()
![]()
Приклад Вирішите рівняння
![]()
Рішення. Перетворимо рівняння до однорідного
![]()
![]()
Розділимо обидві частини рівняння на ![]() , одержимо рівняння:
, одержимо рівняння:
![]()
Нехай ![]() , тоді приходимо до квадратного рівняння
, тоді приходимо до квадратного рівняння
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]()
![]()
Відповідь. ![]() .
.
Приклад Вирішите рівняння
![]()
Рішення
Зведемо обидві частини рівняння у квадрат, з огляду на, що вони мають позитивні значення:
![]() ,
, ![]()
![]()
![]()
Нехай ![]() , тоді одержимо
, тоді одержимо
![]() ,
, ![]() ,
, ![]()
![]()
Відповідь. ![]()
Рівняння, розв'язувані за допомогою тотожностей
![]()
Корисно знати наступні формули
![]() (??)
(??)
Приклад Вирішити рівняння
![]()
Рішення. Використовуючи (??), одержуємо
![]()
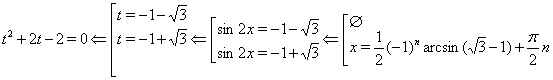
Відповідь. ![]()
Пропонуємо не самі формули, а спосіб їхнього висновку:
![]()
отже,
![]()
Аналогічно, ![]() .
.
Приклад Вирішити рівняння ![]() .
.
Рішення. Перетворимо вираження
![]() :
:
![]() .
.
Рівняння запишеться у вигляді
![]()
Приймаючи ![]() , одержуємо
, одержуємо
![]() .
. ![]() ,
, ![]() . Отже
. Отже
Відповідь. ![]() .
.
Універсальна тригонометрична підстановка
Тригонометричне рівняння виду
![]()
де ![]() --- раціональна функція за допомогою формул (??) -- (??), а так само за допомогою формул (??)-- (??) можна звести до раціонального рівняння щодо аргументів
--- раціональна функція за допомогою формул (??) -- (??), а так само за допомогою формул (??)-- (??) можна звести до раціонального рівняння щодо аргументів ![]() ,
, ![]() ,
, ![]() ,
, ![]() , після чого рівняння може бути зведене до алгебраїчного раціонального рівняння відносно
, після чого рівняння може бути зведене до алгебраїчного раціонального рівняння відносно
![]()
за допомогою формул універсальної тригонометричної підстановки
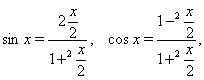 (??)
(??)
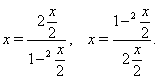 (??)
(??)
Слід зазначити, що застосування формул (??) може приводити до звуження ОДЗ вихідного рівняння, оскільки ![]() не визначений у крапках
не визначений у крапках ![]() , тому в таких випадках потрібно перевіряти, чи є кути
, тому в таких випадках потрібно перевіряти, чи є кути ![]() , коріннями вихідного рівняння.
, коріннями вихідного рівняння.
Приклад Вирішити рівняння
![]()
Рішення. За умовою задачі ![]() . Застосувавши формули (??) й зробивши заміну
. Застосувавши формули (??) й зробивши заміну ![]() , одержимо
, одержимо
![]()
звідки ![]() й, отже,
й, отже, ![]() .
.
Рівняння виду
![]()
Рівняння виду
![]()
де ![]() --- багаточлен, вирішуються за допомогою замін невідомих
--- багаточлен, вирішуються за допомогою замін невідомих
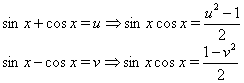 (??)
(??)
Приклад Вирішити рівняння
![]()
Рішення. Зробивши заміну (??) й з огляду на, що
![]() , одержимо
, одержимо
![]()
звідки ![]() ,
, ![]() .
. ![]() - сторонній корінь, тому що
- сторонній корінь, тому що
![]()
Коріннями рівняння
![]() є
є ![]() .
.
НЕСТАНДАРТНІ ТРИГОНОМЕТРИЧНІ РІВНЯННЯ
Використання обмеженості функцій
У практиці тестування не так вуж рідко зустрічаються рівняння, рішення яких ґрунтується на обмеженості функцій ![]() і
і ![]() . Наприклад:
. Наприклад:
Приклад Вирішити рівняння ![]() .
.
Рішення. Оскільки
![]() ,
, ![]()
те ліва частина не перевершує ![]() й дорівнює
й дорівнює ![]() , якщо
, якщо
![]()
Для знаходження значень ![]() , що задовольняють обом рівнянням, надійдемо в такий спосіб. Вирішимо одне з них, потім серед знайдених значень відберемо ті, які задовольняють і іншому
, що задовольняють обом рівнянням, надійдемо в такий спосіб. Вирішимо одне з них, потім серед знайдених значень відберемо ті, які задовольняють і іншому
Почнемо із другого:
![]() ,
, ![]()
Тоді ![]() ,
, ![]() .
.
Зрозуміло, що лише для парних ![]() буде
буде ![]() .
.
Відповідь. ![]() .
.
Інша ідея реалізується при рішенні наступного рівняння:
Приклад Вирішити рівняння
![]() .
.
Рішення. Скористаємося властивістю показової функції
![]() ,
, ![]()
Склавши по членне ці нерівності будемо мати
![]()
Отже ліва частина даного рівняння дорівнює ![]() тоді й тільки тоді, коли виконуються дві рівності
тоді й тільки тоді, коли виконуються дві рівності
![]()
т. е. ![]() може приймати значення
може приймати значення ![]() ,
, ![]() ,
, ![]() , а
, а ![]() може приймати значення
може приймати значення ![]() ,
, ![]() .
.
Відповідь. ![]() ,
, ![]() .
.
Приклад Вирішити рівняння
![]()
Рішення ![]() ,
, ![]() . Отже,
. Отже,
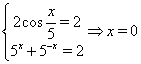
Відповідь. ![]() .
.
Приклад Вирішити рівняння
![]() (??)
(??)
Рішення. Позначимо ![]() , тоді з визначення зворотної тригонометричної функції
, тоді з визначення зворотної тригонометричної функції ![]() маємо
маємо ![]() й
й ![]() .
.
Тому що ![]() , те з рівняння (??) треба нерівність
, те з рівняння (??) треба нерівність ![]() , тобто
, тобто ![]() . Оскільки
. Оскільки ![]() й
й ![]() , те
, те ![]() й
й ![]() . Однак
. Однак ![]() і тому
і тому ![]() .
.
Якщо ![]() й
й ![]() , то
, то ![]() . Тому що раніше було встановлено, що
. Тому що раніше було встановлено, що ![]() , те
, те ![]() .
.
Відповідь. ![]() ,
, ![]() .
.
Приклад Вирішити рівняння
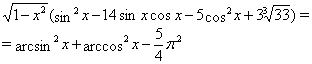 (??)
(??)
Рішення. Областю припустимих значень рівняння (??) є ![]() .
.
Спочатку покажемо, що функція
![]() при будь-яких
при будь-яких ![]() може приймати тільки позитивні значення.
може приймати тільки позитивні значення.
Представимо функцію ![]() в такий спосіб
в такий спосіб
![]()
Оскільки
![]()
те має місце ![]() , тобто
, тобто ![]() .
.
Отже, для доказу нерівності ![]() , необхідно показати, що
, необхідно показати, що
![]()
Із цією метою зведемо в куб обидві частини даної нерівності, тоді
![]()
![]()
![]()
Отримана чисельна нерівність свідчить про те, що ![]() . Якщо при цьому ще врахувати, що
. Якщо при цьому ще врахувати, що ![]() , то ліва частина рівняння (??) ненегативна.
, то ліва частина рівняння (??) ненегативна.
Розглянемо тепер праву частину рівняння (??).
Тому що ![]() , те
, те
![]() .
.
Однак відомо, що
![]()
Звідси треба, що
![]()
тобто права частина рівняння (??) не перевершує ![]() . Раніше було доведено, що ліва частина рівняння (??) ненегативна, тому рівність у (??) може бути тільки в тому випадку, коли обидві його частини рівні
. Раніше було доведено, що ліва частина рівняння (??) ненегативна, тому рівність у (??) може бути тільки в тому випадку, коли обидві його частини рівні ![]() , а це можливо лише при
, а це можливо лише при ![]() .
.
Відповідь. ![]() .
.
Приклад Вирішити рівняння
![]()
Рішення. Позначимо
![]() й
й ![]() .
.
Застосовуючи нерівність Коші-Буняковського, одержуємо
![]()
Звідси треба, що
![]()
C іншої сторони має місце
![]()
Отже, рівняння не має корінь.
Відповідь. ![]() .
.
Приклад Вирішити рівняння
![]()
Рішення. Перепишемо рівняння у вигляді
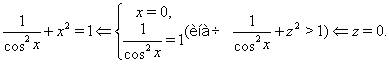
Відповідь. ![]() .
.
Функціональні методи рішення тригонометричних і комбінованих рівнянь
Не всяке рівняння ![]() в результаті перетворень може бути зведене до рівняння того або іншого стандартного виду, для якого існує певний метод рішення. У таких випадках виявляється корисним використовувати такі властивості функцій
в результаті перетворень може бути зведене до рівняння того або іншого стандартного виду, для якого існує певний метод рішення. У таких випадках виявляється корисним використовувати такі властивості функцій ![]() і
і ![]() , як монотонність, обмеженість, парність, періодичність і ін. Так, якщо одна з функцій убуває, а друга зростає на проміжку
, як монотонність, обмеженість, парність, періодичність і ін. Так, якщо одна з функцій убуває, а друга зростає на проміжку ![]() , то при наявності в рівняння
, то при наявності в рівняння ![]() кореня на цьому проміжку, цей корінь єдиний, і тоді його, наприклад, можна знайти підбором. Якщо ж функція
кореня на цьому проміжку, цей корінь єдиний, і тоді його, наприклад, можна знайти підбором. Якщо ж функція ![]() обмежена зверху, причому
обмежена зверху, причому ![]() , а функція
, а функція ![]() обмежена знизу, причому
обмежена знизу, причому ![]() , то рівняння
, то рівняння ![]() рівносильне системі рівнянь
рівносильне системі рівнянь
![]()
Приклад Вирішити рівняння
![]()
Рішення. Перетворимо вихідне рівняння до виду
![]()
і вирішимо його як квадратне відносно ![]() . Тоді одержимо
. Тоді одержимо
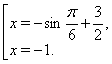
Вирішимо перше рівняння сукупності. Урахувавши обмеженість функції ![]() , доходимо висновку, що рівняння може мати корінь тільки на відрізку
, доходимо висновку, що рівняння може мати корінь тільки на відрізку ![]() . На цьому проміжку функція
. На цьому проміжку функція ![]() зростає, а функція
зростає, а функція ![]() убуває. Отже, якщо це рівняння має корінь, то він єдиний. Підбором знаходимо
убуває. Отже, якщо це рівняння має корінь, то він єдиний. Підбором знаходимо ![]() .
.
Відповідь. ![]() .
.
Приклад Вирішити рівняння
![]()
Рішення. Нехай
![]() ,
, ![]() і
і ![]()
тоді вихідне рівняння можна записати у вигляді функціонального рівняння
![]()
Оскільки
![]()
функція непарна, те
![]() .
.
У такому випадку одержуємо рівняння
![]()
Тому що ![]() ,
, ![]() і
і ![]()
монотонна на
![]()
те рівняння
![]() рівносильне рівнянню
рівносильне рівнянню
![]() , тобто
, тобто ![]() , що має єдиний корінь
, що має єдиний корінь ![]() .
.
Відповідь. ![]()
Приклад Вирішити рівняння
![]()
Рішення. На підставі теореми про похідну складну функцію ясно, що функція ![]() убутна (функція
убутна (функція ![]() убутна,
убутна, ![]() зростаюча,
зростаюча, ![]() убутна). Звідси зрозуміло, що функція
убутна). Звідси зрозуміло, що функція ![]() певна на
певна на ![]() , що убуває. Тому дане рівняння має не більше одного кореня. Тому що
, що убуває. Тому дане рівняння має не більше одного кореня. Тому що ![]() , те
, те
Відповідь. ![]() .
.
Приклад Вирішити рівняння ![]() .
.
Рішення. Розглянемо рівняння на трьох проміжках.
а) Нехай ![]() . Тоді на цій множині вихідне рівняння рівносильне рівнянню
. Тоді на цій множині вихідне рівняння рівносильне рівнянню ![]() . Яке на проміжку
. Яке на проміжку ![]() рішень не має, тому що
рішень не має, тому що ![]() ,
, ![]() , а
, а ![]() . На проміжку
. На проміжку ![]() вихідне рівняння так само не має корінь, тому що
вихідне рівняння так само не має корінь, тому що ![]() , а
, а ![]() .
.
б) Нехай ![]() . Тоді на цій множині вихідне рівняння рівносильне рівнянню
. Тоді на цій множині вихідне рівняння рівносильне рівнянню
![]()
коріннями якого на проміжку ![]() є числа
є числа ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
в) Нехай ![]() . Тоді на цій множині вихідне рівняння рівносильне рівнянню
. Тоді на цій множині вихідне рівняння рівносильне рівнянню
![]()
Яке на проміжку ![]() рішень не має, тому що
рішень не має, тому що ![]() , а
, а ![]() . На проміжку
. На проміжку ![]() рівняння так само рішень не має, тому що
рівняння так само рішень не має, тому що
![]() ,
, ![]() , а
, а ![]()
Відповідь. ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Метод симетрії
Метод симетрії зручно застосовувати, коли у формулюванні завдання присутня вимога одиничності рішення рівняння, нерівності, системи й т.п. або точна вказівка числа рішень. При цьому варто виявити яку-небудь симетрію заданих виражень.
Потрібно також ураховувати різноманіття різних можливих видів симетрії.
Не менш важливим є чітке дотримання логічних етапів у міркуваннях із симетрією.
Звичайно симетрія дозволяє встановити лише необхідні умови, а потім потрібна перевірка їхньої достатності.
Приклад Знайти всі значення параметра ![]() , при яких рівняння
, при яких рівняння
![]() має єдине рішення.
має єдине рішення.
Рішення. Помітимо, що ![]() й
й ![]() --- парні функції, тому ліва частина рівняння є парна функція.
--- парні функції, тому ліва частина рівняння є парна функція.
Значить якщо ![]() --- рішення рівняння, тобто
--- рішення рівняння, тобто ![]() також рішення рівняння. Якщо
також рішення рівняння. Якщо ![]() --- єдине рішення рівняння, те, необхідно,
--- єдине рішення рівняння, те, необхідно, ![]() .
.
Відберемо можливі значення ![]() , зажадавши, щоб
, зажадавши, щоб ![]() було коренем рівняння.
було коренем рівняння.
![]()
Відразу ж відзначимо, що інші значення ![]() не можуть задовольняти умові задачі.
не можуть задовольняти умові задачі.
Але поки не відомо, чи всі відібрані ![]() в дійсності задовольняють умові задачі.
в дійсності задовольняють умові задачі.
Достатність
1) ![]() , рівняння прийме вид
, рівняння прийме вид ![]() .
.
2) ![]() , рівняння прийме вид:
, рівняння прийме вид:
![]()
Очевидно, що ![]() , для всіх
, для всіх ![]() і
і ![]()
Отже, останнє рівняння рівносильне системі:
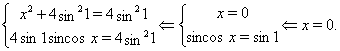
Тим самим, ми довели, що при ![]() , рівняння має єдине рішення.
, рівняння має єдине рішення.
Відповідь. ![]() .
.
тригонометричний рівняння комбінований графічний
Рішення з дослідженням функції
Приклад [??] Доведіть, що всі рішення рівняння
![]()
і- цілі числа.
Рішення. Основний період вихідного рівняння дорівнює ![]() . Тому спочатку досліджуємо це рівняння на відрізку
. Тому спочатку досліджуємо це рівняння на відрізку
![]()
Перетворимо рівняння до виду
![]()
За допомогою мікрокалькулятора одержуємо
![]()
Знаходимо
![]()
Якщо ![]() , то з попередніх рівностей одержуємо
, то з попередніх рівностей одержуємо
![]()
Вирішивши отримане рівняння, одержимо
![]()
Виконані обчислення представляють можливість припустити, що коріннями рівняння, що належать відрізку
![]() , є
, є ![]() ,
, ![]() і
і ![]()
Безпосередня перевірка підтверджує цю гіпотезу. Таким чином, доведено, що коріннями рівняння є тільки цілі числа
![]() ,
, ![]()
Приклад Вирішите рівняння ![]()
Рішення. Знайдемо основний період рівняння. У функції ![]() основний період дорівнює
основний період дорівнює ![]() . Основний період функції
. Основний період функції ![]() дорівнює
дорівнює ![]() . Найменше загальне кратне чисел
. Найменше загальне кратне чисел ![]() і
і ![]() дорівнює
дорівнює ![]() . Тому основний період рівняння дорівнює
. Тому основний період рівняння дорівнює ![]() . Нехай
. Нехай ![]() .
.
Очевидно, ![]() є рішенням рівняння. На інтервалі
є рішенням рівняння. На інтервалі ![]() . Функція
. Функція ![]() негативна. Тому інших корінь рівняння варто шукати тільки на інтервалах
негативна. Тому інших корінь рівняння варто шукати тільки на інтервалах
![]() і
і ![]()
За допомогою мікрокалькулятора спочатку знайдемо наближені значення корінь рівняння. Для цього становимо таблицю значень функції
![]()
на інтервалах
![]() і
і ![]() ; тобто на інтервалах
; тобто на інтервалах ![]() і
і ![]()
| |
|
|
|
| 0 | 0 | 202,5 | 0,85355342 |
| 3 | -0,00080306 | 207 | 0,6893642 |
| 6 | -0,00119426 | 210 | 0,57635189 |
| 9 | -0,00261932 | 213 | 0,4614465 |
| 12 | -0,00448897 | 216 | 0,34549155 |
| 15 | -0,00667995 | 219 | 0,22934931 |
| 18 | -0,00903692 | 222 | 0,1138931 |
| 21 | -0,01137519 | 225 | 0,00000002 |
| 24 | -0,01312438 | 228 | -0,11145712 |
| 27 | -0,01512438 | 231 | -0,21961736 |
| 30 | -0,01604446 | 234 | -0,32363903 |
| 33 | -0,01597149 | 237 | -0,42270819 |
| 36 | -0,01462203 | 240 | -0,5160445 |
| 39 | -0,01170562 | 243 | -0,60290965 |
| 42 | -0,00692866 | 246 | -0,65261345 |
| 45 | 0,00000002 | 249 | -0,75452006 |
| 48 | 0,00936458 | 252 | -0,81805397 |
| 51 | 0,02143757 | 255 | -0,87270535 |
| 54 | 0,03647455 | 258 | -0,91803444 |
| 57 | 0,0547098 | 261 | -0,95367586 |
| 60 | 0,07635185 | 264 | -0,97934187 |
| 63 | 0,10157893 | 267 | -0,99482505 |
| 66 | 0,1305352 | 270 | -1 |
| 67,5 | 0,14644661 |
З таблиці легко вбачаються наступні гіпотези: коріннями рівняння, що належать відрізку ![]() , є числа:
, є числа: ![]() ;
; ![]() ;
; ![]() . Безпосередня перевірка підтверджує цю гіпотезу.
. Безпосередня перевірка підтверджує цю гіпотезу.
Відповідь. ![]() ;
; ![]() ;
; ![]() .
.
ТРИГОНОМЕТРИЧНІ НЕРІВНОСТІ
Рішення тригонометричних нерівностей за допомогою одиничної окружності
При рішенні тригонометричних нерівностей виду
![]()
де ![]() --- одна із тригонометричних функцій, зручно використовувати тригонометричну окружність для того, щоб найбільше наочно представити рішення нерівності й записати відповідь. Основним методом рішення тригонометричних нерівностей є відомість їх до найпростіших нерівностей типу
--- одна із тригонометричних функцій, зручно використовувати тригонометричну окружність для того, щоб найбільше наочно представити рішення нерівності й записати відповідь. Основним методом рішення тригонометричних нерівностей є відомість їх до найпростіших нерівностей типу ![]() . Розберемо на прикладі, як вирішувати такі нерівності.
. Розберемо на прикладі, як вирішувати такі нерівності.
Приклад Вирішите нерівність ![]() .
.
Рішення. Намалюємо тригонометричну окружність і відзначимо на ній крапки, для яких ордината перевершує ![]()

Для
![]()
рішенням даної нерівності будуть
![]() .
.
Ясно також, що якщо деяке число ![]() буде відрізнятися від якого-небудь числа із зазначеного інтервалу на
буде відрізнятися від якого-небудь числа із зазначеного інтервалу на ![]() , те
, те ![]() також буде не менше
також буде не менше ![]() . Отже, до кінців знайденого відрізка рішення потрібно просто додати
. Отже, до кінців знайденого відрізка рішення потрібно просто додати ![]() . Остаточно, одержуємо, що рішеннями вихідної нерівності будуть усе
. Остаточно, одержуємо, що рішеннями вихідної нерівності будуть усе
![]()
Відповідь. ![]()
Для рішення нерівностей з тангенсом і котангенсом корисне поняття про лінію тангенсів і котангенсів. Такими є прямі ![]() й
й ![]() відповідно (на малюнку (1) і (2)), що стосуються тригонометричної окружності.
відповідно (на малюнку (1) і (2)), що стосуються тригонометричної окружності.
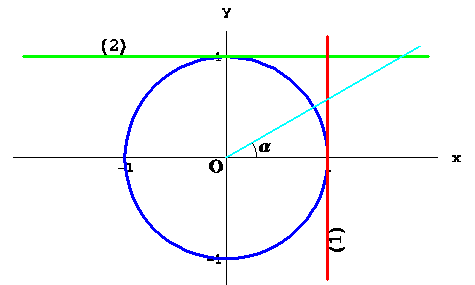
Легко помітити, що якщо побудувати промінь із початком на початку координат, що становить кут ![]() з позитивним напрямком осі абсцис, то довжина відрізка від крапки
з позитивним напрямком осі абсцис, то довжина відрізка від крапки ![]() до крапки перетинання цього променя з лінією тангенсів у точності дорівнює тангенсу кута, що становить цей промінь із віссю абсцис. Аналогічне спостереження має місце й для котангенса.
до крапки перетинання цього променя з лінією тангенсів у точності дорівнює тангенсу кута, що становить цей промінь із віссю абсцис. Аналогічне спостереження має місце й для котангенса.
Приклад Вирішите нерівність
![]()
Рішення
Позначимо ![]() , тоді нерівність прийме вид найпростішого:
, тоді нерівність прийме вид найпростішого: ![]() . Розглянемо інтервал
. Розглянемо інтервал ![]() довжиною, рівної найменшому позитивному періоду (НПП) тангенса. На цьому відрізку за допомогою лінії тангенсів установлюємо, що
довжиною, рівної найменшому позитивному періоду (НПП) тангенса. На цьому відрізку за допомогою лінії тангенсів установлюємо, що ![]() . Згадуємо тепер, що необхідно додати
. Згадуємо тепер, що необхідно додати ![]() , оскільки НПП функції
, оскільки НПП функції ![]()
![]() . Отже,
. Отже,
![]()
Вертаючись до змінного ![]() , одержуємо, що
, одержуємо, що
![]()
Відповідь. ![]()
Нерівності зі зворотними тригонометричними функціями зручно вирішувати з використанням графіків зворотних тригонометричних функцій. Покажемо, як це робиться на прикладі.
Рішення тригонометричних нерівностей графічним методом
Помітимо, що якщо ![]() --- періодична функція, то для рішення нерівності
--- періодична функція, то для рішення нерівності ![]()
![]() необхідно знайти його рішення на відрізку, довжина якого дорівнює періоду функції
необхідно знайти його рішення на відрізку, довжина якого дорівнює періоду функції ![]() . Всі рішення вихідної нерівності будуть складатися зі знайдених значень
. Всі рішення вихідної нерівності будуть складатися зі знайдених значень ![]() , а також всіх
, а також всіх ![]() , що відрізняються від знайдених на будь-яке ціле число періодів функції
, що відрізняються від знайдених на будь-яке ціле число періодів функції ![]() .
.
Розглянемо рішення нерівності ![]() (
(![]() ).
).
Оскільки ![]() , те при
, те при ![]() нерівність рішень не має. Якщо
нерівність рішень не має. Якщо ![]() , то множина рішень нерівності
, то множина рішень нерівності ![]() --- множина всіх дійсних чисел.
--- множина всіх дійсних чисел.
Нехай ![]() . Функція синус має найменший позитивний період
. Функція синус має найменший позитивний період ![]() , тому нерівність
, тому нерівність ![]() можна вирішити спочатку на відрізку довжиною
можна вирішити спочатку на відрізку довжиною ![]() , наприклад, на відрізку
, наприклад, на відрізку
![]()
Будуємо графіки функцій
![]() і
і ![]() (
(![]() )
)
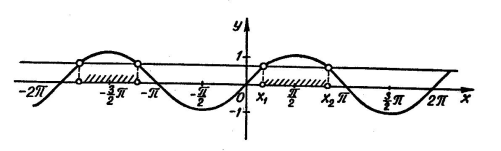
На відрізку ![]() функція синус зростає, і рівняння
функція синус зростає, і рівняння ![]() , де
, де ![]() , має один корінь
, має один корінь ![]() . На відрізку
. На відрізку ![]() функція синус убуває, і рівняння
функція синус убуває, і рівняння ![]() має корінь
має корінь ![]() . На числовому проміжку
. На числовому проміжку ![]() графік функції
графік функції ![]() розташована вище графіка функції
розташована вище графіка функції ![]() . Тому для всіх
. Тому для всіх ![]() із проміжку
із проміжку ![]() ) нерівність
) нерівність ![]() виконується, якщо
виконується, якщо ![]() . У силу періодичності функції синус всі рішення нерівності
. У силу періодичності функції синус всі рішення нерівності ![]() задаються нерівностями виду:
задаються нерівностями виду:
![]()
Аналогічно вирішуються нерівності ![]() ,
, ![]() , і т.п.
, і т.п.
Приклад Вирішимо нерівність ![]() .
.
Рішення. Розглянемо графік функції ![]()
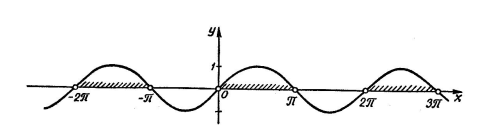
і виберемо із проміжку ![]() на осі
на осі ![]() значення аргументу
значення аргументу ![]() , яким відповідають крапки графіка, що лежать вище осі
, яким відповідають крапки графіка, що лежать вище осі ![]() . Таким проміжком є інтервал
. Таким проміжком є інтервал ![]() . З огляду на періодичність функції
. З огляду на періодичність функції ![]() всі рішення нерівності
всі рішення нерівності ![]() можна записати так:
можна записати так:
![]()
Відповідь. ![]()
Приклад Вирішите нерівність ![]() .
.
Рішення. Намалюємо графік функції ![]() . Знайдемо крапку перетинання цього графіка з горизонтальної прямої
. Знайдемо крапку перетинання цього графіка з горизонтальної прямої ![]() .
.
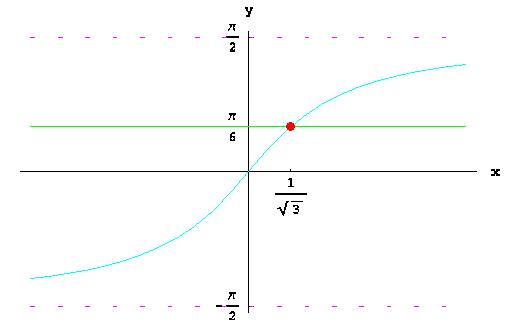
Це крапка з абсцисою ![]() . За графіком видно, що для всіх
. За графіком видно, що для всіх ![]() графік функції лежить нижче прямій
графік функції лежить нижче прямій ![]() . Отже, ці
. Отже, ці ![]() й становлять:
й становлять:
Відповідь. ![]()
ВІДБІР КОРНІВ
Проблема відбору корнів, відсівання зайвих корнів при рішенні тригонометричних рівнянь досить специфічна й звичайно виявляється більше складної, чим це мало місце для рівнянь алгебраїчних. Приведемо рішення рівнянь, що ілюструють типові випадки появи сторонніх корнів і методи <<боротьби>> з ними.
Приклад Знайти найближчий до числа ![]() корінь рівняння
корінь рівняння
![]()
Рішення
![]()
![]()
![]()
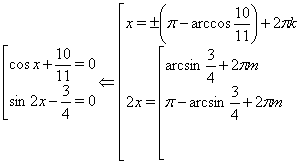
Підставляючи послідовно у формул
![]()
замість змінної ![]() виписані вище серії рішень рівнянь, відшукаємо для кожної з них
виписані вище серії рішень рівнянь, відшукаємо для кожної з них ![]() , а потім зрівняємо отримані мінімальні
, а потім зрівняємо отримані мінімальні ![]() між собою
між собою
a) ![]()
Ясно, що ![]() досягається при
досягається при ![]() , тобто
, тобто ![]()
б)![]()
![]() .
.
в)![]() .
.
г)![]() .
.
![]() .
.
Виберемо мінімальне із чисел ![]() ,
, ![]() . Відразу ясно, що
. Відразу ясно, що ![]() й що
й що ![]() . Залишилося зрівняти
. Залишилося зрівняти ![]() й
й ![]() . Припустимо, що
. Припустимо, що
![]()
![]()
![]()
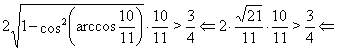
![]()
Остання нерівність --- вірне, а всі зроблені переходи --- рівносильні. Тому вірно вихідна нерівність. Обґрунтуємо рівносиль переходів (*) і (**) (рівносиль інших переходів треба із загальних властивостей числових нерівностей). У випадку перетворення (*), досить помітити, що числа ![]() й
й ![]() розташований на ділянці
розташований на ділянці ![]() монотонного зростання функції
монотонного зростання функції ![]() . У випадку переходу (**) формула
. У випадку переходу (**) формула ![]() справедлива, тому що
справедлива, тому що
![]()
Відповідь. ![]()
Приклад Знайти корінь рівняння: ![]() .
.
Рішення цього рівняння розпадається на два етапи: 1) рішення рівняння, що виходить із даного піднесенням у квадрат обох його частин; 2) відбір тих корінь, які задовольняють умові ![]() . При цьому піклується про умову
. При цьому піклується про умову ![]() немає необхідності. Всі значення
немає необхідності. Всі значення ![]() , що задовольняють зведеному у квадрат рівнянню, цій умові задовольняють.
, що задовольняють зведеному у квадрат рівнянню, цій умові задовольняють.
Перший крок нас приводить до рівняння ![]() , звідки
, звідки
![]()
Тепер треба визначити, при яких ![]() буде
буде
![]()
Для цього досить для ![]() розглянути значення
розглянути значення ![]() ,
, ![]() ,
, ![]() , тобто <<обійти один раз коло>>, оскільки далі значення косинуса почнуть повторюватися, що вийшли кути будуть відрізнятися від уже розглянутих на величину, кратну
, тобто <<обійти один раз коло>>, оскільки далі значення косинуса почнуть повторюватися, що вийшли кути будуть відрізнятися від уже розглянутих на величину, кратну ![]()
Відповідь. ![]() ,
, ![]()
Отже, основна схема відбору корнів полягає в наступному. Перебуває найменший загальний період всіх тригонометричних функцій вхідних у рівняння. На цьому періоді відбираються коріння, а потім, що залишилися коріння, періодично тривають.
Приклад Вирішити рівняння
![]()
Рішення. Рівняння рівносильне змішаній системі
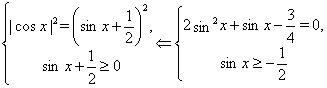
![]()
Але ![]() - не годиться.
- не годиться.
Відповідь. ![]() .
.
Розкриваючи знак модуля одержуємо більше громохке рішення. А відповідь у цьому випадку приймає вид:
Відповідь. ![]()
ЗАДАЧІ ДЛЯ САМОСТІЙНОГО РІШЕННЯ
Тест по темі <<Тригонометричні рівняння>>
• Об'єднання яких множин ![]() ,
, ![]() ,
, ![]() ,
, ![]() є рішенням рівняння
є рішенням рівняння
![]()
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
a) ![]() ,
, ![]() б)
б) ![]() ,
, ![]() в)
в) ![]() ,
, ![]() г)
г) ![]() ,
, ![]()
• Вирішите рівняння![]()
a)![]() б)
б)![]() в)
в) ![]() г)
г) ![]()
• Вирішите рівняння ![]()
a) ![]()
б) ![]()
в) ![]()
г) ![]()
• Вирішите рівняння ![]()
a) ![]()
б) ![]()
в) ![]()
г) ![]()
Вирішите рівняння ![]()
a) ![]()
б) ![]()
в) ![]()
г) ![]()
• Серед множин ![]() ,
, ![]() знайдіть рішення рівняння
знайдіть рішення рівняння
![]()
і вкажіть ті, які не є підмножинами один одного.
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
• Серед множин ![]() ,
, ![]() знайдіть рішення рівняння
знайдіть рішення рівняння
![]()
![]()
![]()
![]()
![]()
а) ![]() б)
б) ![]() в)
в) ![]() г)
г)![]()
• Вирішите рівняння
![]()
а) ![]() б)
б) ![]()
в) ![]() г)
г) ![]()
• Вирішите рівняння
![]()
а) ![]()
б) ![]()
в) ![]()
г) ![]()
• Вирішите рівняння
![]() .
.
а) ![]() б)
б) ![]()
в) ![]() г)
г) ![]()
• Сума корінь рівняння ![]() на відрізку
на відрізку ![]() дорівнює:
дорівнює:
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
• Вирішите рівняння
![]()
У відповіді записати кількість корінь рівняння, що належать відрізку
![]()
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
• Вирішити рівняння ![]()
а) ![]() б)
б) ![]()
в) ![]() г)
г) ![]()
• Вирішите рівняння ![]() .
.
a) ![]() б)
б) ![]()
в) ![]() г)
г) ![]()
• Вирішите рівняння ![]()
a) ![]()
б) ![]()
в) ![]()
г) ![]()
Знайдіть найбільший негативний корінь рівняння
![]()
a) ![]() б)
б) ![]()
в) ![]() г)
г) ![]()
• Вирішите рівняння ![]() на множині
на множині ![]()
a) ![]()
б) ![]()
в) ![]()
г) ![]()
• Вирішите рівняння ![]()
a) ![]() б)
б) ![]()
в) ![]() г)
г) ![]()
• Вирішити рівняння ![]()
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
• Вирішите рівняння ![]()
a) ![]()
б) ![]() або
або ![]()
в) ![]() або
або ![]() й
й ![]()
г) ![]() або
або ![]() й
й ![]()
Відповіді 1а 2б 3б 4г 5б 6б 7а 8б 9г 10б 11а 12б 13в або г 14а 15в 16в 17в 18а або б 19г 20в
ВИСНОВОК
У даній роботі були розглянуті методи рішення тригонометричних рівнянь і нерівностей, як найпростіших, так і рівня олімпіади. Були розглянуті основні методи рішення тригонометричних рівнянь і нерівностей, причому, як специфічні -і- характерні тільки для тригонометричних рівнянь і нерівностей,-і- так і загальні функціональні методи рішення рівнянь і нерівностей, стосовно до тригонометричних рівнянь.
У дипломній роботі наведені основні теоретичні відомості: визначення й властивості тригонометричних і зворотних тригонометричних функцій; вираження тригонометричних функцій через інші тригонометричні функції, що дуже важливо для перетворення тригонометричних виражень, що особливо містять зворотні тригонометричні функції; крім основних тригонометричних формул, добре відомих зі шкільного курсу, наведені формули вираження, що спрощують, утримуючі зворотні тригонометричні функції. Розглянуто рішення елементарних тригонометричних рівнянь, метод розкладання на множники, методи відомості тригонометричних рівнянь до алгебраїчного. Через те, що рішення тригонометричних рівнянь можна записати декількома способами, і вид цих рішень не дозволяє відразу встановити, чи є ці рішення однаковими або різними, розглянута загальна схема рішення тригонометричних рівнянь і докладно розглянуте перетворення груп загальних рішень тригонометричних рівнянь. Докладно розглянуті методи рішення елементарних тригонометричних нерівностей, як на одиничній окружності, так і графічним методом. Описано процес рішення неелементарних тригонометричних нерівностей через елементарні нерівності й уже добре відомий школярам метод інтервалів. Наведено рішення типових завдань на відбір корнів. Наведено необхідні теоретичних відомості для відбору корнів: розбивка множини цілих чисел на непересічні підмножини, рішення рівнянь у цілих числах.
Результати даної дипломної роботи можуть бути використані як навчальний матеріал при підготовці курсових і дипломних робіт, при складанні факультативів для школярів, так само робота може застосовуватися при підготовці учнів до вступних іспитів зовнішнього оцінювання.
СПИСОК ДЖЕРЕЛ
[1] Вигодський Я.Я., Довідник по елементарній математиці. – К., 2003
[2] Ігудисман О., Математика на усному іспиті. – К., 2001.
[3] Азаров А.І., Рівняння., - К., 2005
[4] Литвиненко В.Н., Практикум по елементарній математиці. – К., 2000
[5] Шаригін І.Ф., Факультативний курс по математиці: рішення задач. – К., 2000
[6] Бардушкин В., Тригонометричні рівняння. Відбір корнів. – К., 2005
[7] Василевський А.Б., Завдання для позакласної роботи з математики. – К., 2005
[8]Сапунів П. І., Перетворення й об'єднання груп загальних рішень тригонометричних рівнянь. – К., 2003
[9]Самусенко А.В., Математика: Типові помилки абітурієнтів. – К., 1991.
Похожие работы
... що найбільший теоретичний і прикладний інтерес представляє випадок викладений у другому розділі. Розділ 2 Всі результати першого розділу, що стосуються дзета-функції Римана, були отримані в припущенні, що її аргумент s – дійсне число. Однак, найвидатніші дослідження й численні важливі додатки стали можливі лише після включення в область визначення функції комплексних чисел. Уперше розглянув ...
... нтуватися на використання підручників [53; 54; 5]. У класах фізико-математичного спрямування доцільно орієнтуватись на використання підручників [53; 54; 5; 1]. РОЗДІЛ 2 ОСОБЛИВОСТІ ВИВЧЕННЯ МАТЕМАТИКИ У ПРОФІЛЬНИХ КЛАСАХ В СУЧАСНИХ УМОВАХ 2.1. ОСНОВНІ ПОЛОЖЕННЯ ПРОФІЛЬНОЇ ДИФЕРЕНЦІАЦІЇ НАВЧАННЯ МАТЕМАТИКИ Математика є універсальною мовою, яка широко застосовується в усіх ...
... навчальних досягнень учнів в умовах модульного навчання” розкриті загальні питання експериментальної роботи, обґрунтовані необхідні дидактичні умови організації перевірки ефективності моделей оцінювання навчальних досягнень старшокласників в умовах модульного навчання. У процесі дослідження були змодельовані контрольно-оцінювальні системи навчальних досягнень старшокласників, що адаптовані до ...
... Зауваження. Отже, при рішенні рівнянь із радикалами потрібне вміти користуватися кожним із цих методів і вибирати в кожному випадку оптимальний. 3. Не стандартні методи рішення ірраціональних рівнянь Існують ірраціональні рівняння, які вважаються для школярів звичайних освітніх шкіл задачами підвищених труднощів. Для рішення таких рівнянь краще застосовувати не традиційні методи, а прийоми, ...

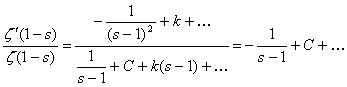
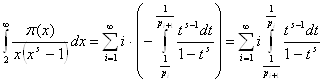
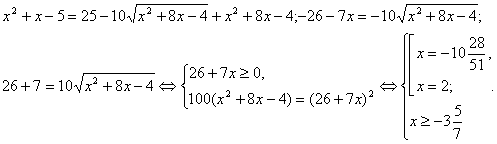
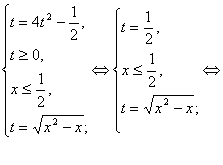
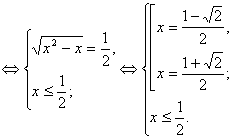
0 комментариев