Навигация
Сложение, умножение и свертывание объектов
9984
знака
0
таблиц
0
изображений
3. Сложение, умножение и свертывание объектов
В алгебре объектов со многими индексами имеются три главные операции, которые называются сложением, умножением и свертыванием.
а) Сложение. Эта операция применима только к объектам одного и того же порядка и типа. Если нам даны два объекта одного и того же порядка и типа и если мы складываем каждую составляющую первого объекта с соответствующей составляющей второго, то мы, очевидно, приходим к объекту того же порядка и типа, что и слагаемые. Этот процесс есть операция сложения, и результирующий объект называется суммой двух объектов. Таким образом, если arst и brst — два объекта третьего порядка, то объект 
, определенный равенством
есть сумма 
и 
. Мы подразумеваем здесь алгебраическую сумму; поэтому вычитание включено сюда как частный случай. Кроме того, эта операция может быть распространена непосредственно на случай любого количества объектов, если только они все одного и того же порядка и типа.
б) Умножение. Мы сейчас определим произведение двух объектов. Если мы берем два объекта любого типа и умножаем каждую составляющую первого объекта на каждую составляющую второго, мы получаем объект, порядок которого равен сумме порядков двух исходных объектов; этот результирующий объект называется произведением двух объектов. Например, если arst — объект третьего порядка и bmn — объект второго порядка, то мы видим, что объект сrmn, составляющие которого определяются равенством
есть объект пятого порядка и является произведением arst и bmn. Этот процесс, конечно, может быть распространен на любое количество объектов.
в) Свертывание. Процесс свертывания может быть пояснен на примере. Возьмем объект пятого порядка
который имеет как верхние, так и нижние индексы. Если мы теперь положим и равным р, мы получим объект arsfp, и так как р является теперь повторяющимся индексом, то необходимо произвести суммирование от 1 до 3, в соответствии с нашим условием. Итак, полученный таким путем новый
Мы видим, что наш новый объект A2) —третьего по- рядка, т. е. его порядок на два ниже, чем порядок исходного объекта. Операция может быть, очевидно, повторена несколько раз, т. е. мы можем произвести свертывание относительно любой пары индексов, один из которых является нижним,, а другой—верхним. В приведенном выше примере мы можем произвести свертывание еще раз по индексам rp, получив объект первого порядка
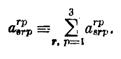
Имеется еще одна операция, называемая внутренним умножением, которая не является новой, так как в действительности она является комбинацией умножения и свертывания. Чтобы выполнить эту операцию над двумя объектами, мы сначала перемножаем их, а затем свертываем произведение по нижнему индексу одного объекта и верхнему индексу другого. Таким образом, внутреннее произведение двух объектов есть, например,
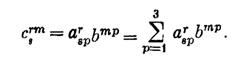
4. Симметричные и антисимметричные объекты
Если мы имеем объект аmn с двумя нижними индексами, то может случиться, что каждая из составляющих не изменится по величине и знаку при перемене мест индексов, т. е.
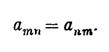
Такой объект называют симметричным. В более общем случае объект, имеющий любое число нижних индексов, называется симметричным относительно двух из них, если составляющие не изменяются при перемене мест этих двух индексов. Объект называется абсолютно симметричным относительно нижних индексов, если при перемене мест любых двух из них составляющие не изменяются. Абсолютно симметричный объект третьего порядка будет, следовательно, удовлетворять соотношениям
С другой стороны, объект аmn называется антисимметричным, если перемена мест индексов изменяет знак составляющей, но не изменяет ее численного значения; в таком случае мы имеем
Эти равенства, выписанные полностью, выглядят так:
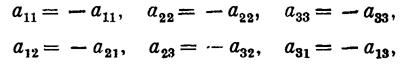
откуда мы немедленно заключаем, что 
Как и выше, объект может быть антисимметричным либо относительно двух каких-нибудь нижних индексов, либо относительно всех пар индексов; в последнем случае объект называется абсолютно антисимметричным. Абсолютно антисимметричный объект третьего порядка должен удовлетворять соотношениям
Все сказанное выше о симметрии и антисимметрии в равной степени применимо и к верхним индексам.
Литература
1. Рашевский П.К., Риманова геометрия и тензорный анализ, Гостехиздат, Москва, 1953.
2. Гуревич Г.В., Основы теории алгебраических инвариантов, Гостехиздат, Москва, 1948.
3. Труды семинара по векторному и тензорному анализу, вып. I—X, Гостехиздат, Москва, 1933, 1956.
4. Каган В.Ф., Основы теории поверхностей, т, 1, Гостехиздат, Москва, 1943, т. Ц, Москва, 1947.
Похожие работы
... ;0,0(p2) = P0,0. В силу теоремы 2.8. главы I разложения I, Р1 и Р2 также определяются однозначно. § 2. Два ортопроектора в сепарабельном гильбертовом пространстве 2.1. Неприводимые *-представления *-алгебры P2 . Пусть А = Р1 - Р1┴ = 2Р1 – I и В = Р2 – Р2┴ = 2Р2 – I. Тогда А2 = I , В2 = I. Следовательно А и В самосопряженные унитарные операторы в Н. Положим U=АВ, тогда U-1=ВА и А-1UА ...
... ;0,0(p2) = P0,0. В силу теоремы 2.8. главы I разложения I, Р1 и Р2 также определяются однозначно. § 2. Два ортопроектора в сепарабельном гильбертовом пространстве 2.1. Неприводимые *-представления *-алгебры P2 . Пусть А = Р1 - Р1┴ = 2Р1 – I и В = Р2 – Р2┴ = 2Р2 – I. Тогда А2 = I , В2 = I. Следовательно А и В самосопряженные унитарные операторы в Н. Положим U=АВ, тогда U-1=ВА и А-1UА = ...
... последняя цифра делится на 2; на 3 или на 9, если сумма цифр делится соответственно на 3 или на 9; на 5, если оно оканчивается на 0 или 5. Единица, наименьшее из натуральных чисел n = 1. В современной математике понятие единицы (единичного элемента) рассматривают в алгебраических структурах более общей природы (напр., группах). Сложение, арифметическое действие. Обозначается знаком + (плюс). В ...
... (5.16) Непосредственное использование оценок погрешности (5.4), (5.8) и (5.12) неудобно, так как при этом требуется вычисление производных функции f(x). В вычислительной практике используются другие оценки. Вычтем из равенства (5.15) равенство (5.16): Ih/2 – Ih » Chk(2k – 1). (5.17) Учитывая приближенное равенство (5.16), получим следующее приближенное ...
0 комментариев