Навигация
Решение систем линейных уравнений
3. Решение систем линейных уравнений
Векторные и матричные операторы и функции позволяют решать широкий круг задач линейной алгебры.
Например, если задана матрица A и вектор B для системы линейных уравнений в матричной форме ![]() , то вектор решения X можно получить из уравнения
, то вектор решения X можно получить из уравнения ![]() .
.
Поскольку решение систем линейных уравнений довольно распространенная задача, то в Mathcad введена специальная функция lsolve(A,B), которая возвращает вектор X для системы линейных уравнений ![]() при заданной матрице коэффициентов A и векторе свободных членов B. Если уравнений n, то размер вектора B должен быть n, а матрицы A - n´n.
при заданной матрице коэффициентов A и векторе свободных членов B. Если уравнений n, то размер вектора B должен быть n, а матрицы A - n´n.
Пусть необходимо решить систему уравнений
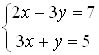 .
.
В нашем случае матрицы A и B определяется следующим образом:
 ,
, 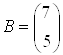 . Два способа решения этой системы уравнений в Matcad приведены на рисунке 2.3.
. Два способа решения этой системы уравнений в Matcad приведены на рисунке 2.3.
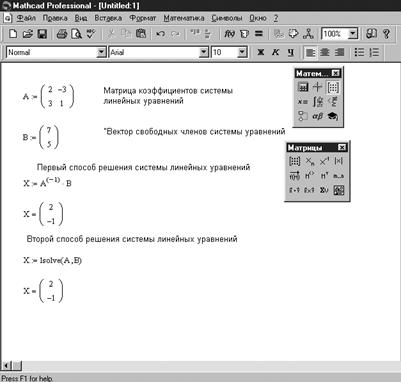
Рис. 2.3. Примеры решения системы линейных уравнений
4. Решение нелинейных уравнений
Многие уравнения, например трансцендентные, не имеют аналитических решений. Однако они могут решаться численными методами с заданной погрешностью (не более значения, заданного системной переменной TOL).
Для уравнений вида ![]() решение находится с помощью следующей функции:
решение находится с помощью следующей функции:
root(Выражение, Имя_переменной).
Эта функция возвращает с заданной точностью значение переменной, при котором выражение равно 0. Функция реализует вычисления итерационным методом, причем можно задать начальное значение переменной. Это особенно полезно если уравнение имеет несколько корней.
Для поиска корней полинома степени n существует специальная функция polyroots(V). Она возвращает вектор всех корней полинома степени n, коэффициенты которого находятся в векторе V, который имеет длину n+1. Заметим, что корни полинома могут быть как вещественными, так и комплексными числами. Не рекомендуется пользоваться этой функцией, если степень полинома выше пятой, поскольку в этом случае трудно получить малую погрешность вычисления корней.
Пример использования функции root приведен на рисунке 2.4, а функции polyroots - на рисунке 2.5.
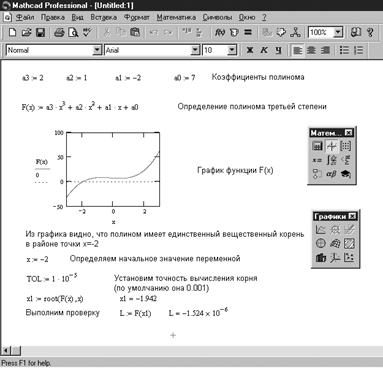
Рис. 2.4. Пример использования функции root
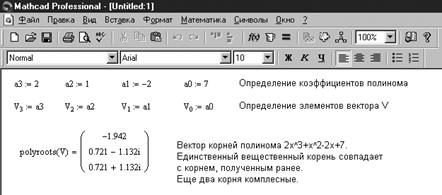
Рис. 2.5. Пример использования функции polyroots
5. Решение систем нелинейных уравнений
При решении систем нелинейных уравнений используется специальный вычислительный блок, открываемый директивой Given и имеющий следующую структуру:
- Начальные условия (задаются в виде переменная:=значение).
- Директива Given.
- Уравнения.
- Ограничительные условия.
- Выражения с функциями Find, Minerr, Maximize, Minimize.
Начальные условия определяют начальные значения искомых переменных. Они задаются обычным присваиванием переменным начальных значений. Если переменных несколько, то используется векторное представление для начальных значений. Уравнения задаются в виде expr_left=expr_right с применением жирного знака равно = между левой и правой частью каждого уравнения (вводится с клавиатуры как Ctrl+= или панели булевых операторов). Ограничительные условия обычно задаются в виде неравенств и равенств, которые должны удовлетворяться при решении уравнений.
В блоке используется одна из следующих функций:
- Find(v1,v2,…,vn) - возвращает значение одной или ряда переменных для точного решения;
- Minerr(v1,v2,…,vn) - возвращает значение одной или ряда переменных для приближенного решения.
Между этими функциями существует принципиальное различие. Первая функция используется, когда решение реально существует, хотя и не является аналитическим. Вторая функция пытается найти наилучшее приближение даже к несуществующему значению путем минимизации среднеквадратичной погрешности решения.
Логические операторы в качестве ограничительных условий вводятся следующим образом:
| Оператор | Клавиши | Описание |
| e1>e2 | e1>e2 | e1 больше e2 |
| e1<e2 | e1<e2 | e1 меньше e2 |
| e1³e2 | e1 Ctrl+) e2 | e1 больше или равно e2 |
| e1£e2 | e1 Ctrl+( e2 | e1 меньше или равно e2 |
| e1¹e2 | e1 Ctrl+# e2 | e1 не равно e2 |
| e1=e2 | e1 Ctrl+= e2 | e1 равно e2 |
В качестве примера рассмотрим решение (рис. 2.6.) следующей системы нелинейных уравнений:
 .
.
mathcad матрица уравнение линейный
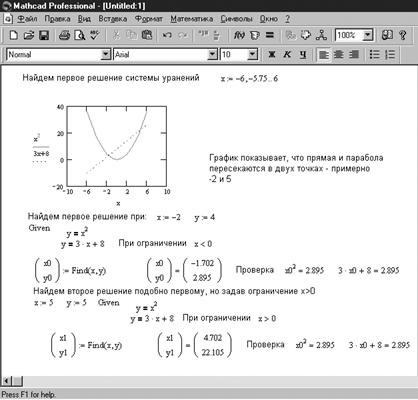
Рис. 2.6. Пример решения системы нелинейных уравнений
При решении системы нелинейных уравнений с использованием функции Minerr надо проявлять осторожность и обязательно проверять полученное решение. Нередки случаи, когда решения могут оказаться ошибочными. Полезно как можно точнее указывать начальные приближения к решению.
Заключение
И так, перечислим основные достоинства MATHCAD`a.
Во-первых, это универсальность пакета MATHCAD, который может быть использован для решения самых разнообразных инженерных, экономических, статистических и других научных задач.
Во-вторых, программирование на общепринятом математическом языке позволяет преодолеть языковой барьер между машиной и пользователем. Потенциальные пользователи пакета - от студентов до академиков.
И в-третьих, совместно применение текстового редактора, формульного транслятора и графического процессора позволяет пользователю в ходе вычислений получить готовый документ.
Но, к сожалению, популярный во всем мире пакет MATHCAD фирмы MathSoft, в России распространен еще слабо, как и все программные продукты подобно рода.
Библиографический список
1. Дьяконов В.П. Matcad 8/2000: Специальный справочник. - СПб.: Питер, 2001. - 592 с.
2. Артемкин Д.Е., Пылькин А.Н. Основы работы в системе MATHCAD. Рязань: Рязанский областной институт развития образования, 1999. - 72 с.
3. Соломоник В.С. Сборник вопросов и задач по математике. - М.: Высшая школа, 1978. - 264 с.
4. Гусев В.А., Мордкович А.Г. Математика : Справочные материалы. - М.: Просвещение, 1988. - 416 с.
Похожие работы
... с единицами измерений физических величин в системе MathCAD? 11. Подробно охарактеризуйте текстовые, графические и математические блоки. Лекция №2. Задачи линейной алгебры и решение дифференциальных уравнений в среде MathCAD В задачах линейной алгебры практически всегда возникает необходимость выполнять различные операции с матрицами. Панель операторов с матрицами находится на панели Math. ...
... 2.4 Массивы Массив — имеющая уникальное имя совокупность конечного числа числовых или символьных элементов, упорядоченных некоторым образом и имеющих определенные адреса. В пакете MathCAD используются массивы двух наиболее распространенных типов: - одномерные (векторы); - двухмерные (матрицы). Вывести шаблон матрицы или вектора можно одним из способов: · ...
... красного и синего нулевые, то вы должны записать #00FF00. И таким образом можно получить все 16 млн. цветов, которые научились воспроизводить современные мониторы. Вопрос №3. СУБД Microsoft Access: создание запросов с параметрами и запросов действия Запросы - важнейший инструмент любой системы управления базами данных (СУБД). Они служат для выборки определенных записей из базы, ...
... численных методов (при решении реальных, а не учебных задач!) предполагает использование компьютеров с достаточным быстродействием. Использование для численного решения дифференциальных уравнений компьютерного пакета MathCAD предполагает знание алгоритма работы численных методов для разумного их применения (знание границ применимости, оценки точности, затрат компьютерных ресурсов и др.). Дело в ...
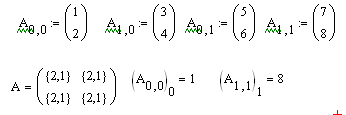



0 комментариев