Проблемы формирования и использования финансовых ресурсов

7. Проблемы формирования и использования финансовых ресурсов

 

Экономический кризис наиболее остро отразился на реальном векторе экономики, характеризующемся деградацией его структуры, беспрецедентным падением объемов производства, параличом инвестиционной деятельности предприятий, ослаблением научно-технического потенциала промышленности, расстройством финансовой системы общественного воспроизводства. Основными причинами этого являются углубление диспропорций в развитии реального сектора и сферы обращения (отток финансовых ресурсов из материального производства в процессе «ваучерной» приватизации, изъятие свободных этапов через рынок ГКО), не разработанность правовых норм регулирования некоторых видов экономической деятельности.

В настоящее время для большинства предприятий первоочередными стали задачи поддержания устойчивого производства стабилизации текущей финансовой деятельности. Вопросы же стратегического развития, инвестиций в основное производство в некоторой мере отошли на второй план. Ключевой проблемой, обусловившей снижение текущей финансовой устойчивости предприятий, является дефицит денежных оборотных средств, необходимых для обеспечения текущего производства. Основными порами, сдерживающими развитие предприятий, стали, с одной стороны, неплатежи покупателей, с другой стороны - большая доля денежной составляющей в расчетах за поставленную продукцию.

За последние годы произошли изменения в структуре источников финансовых ресурсов. Восполнение потерь от снижения доходов по основной хозяйственной деятельности в большинстве отраслей стало долечиваться главным образом за счет поступлений от операций по основной деятельности, что было обусловлено их усиливающейся, ориентацией на зарубежные рынки сбыта и операции с валютой, активным выходом на финансовые спекулятивные рынки, расширением практики «натурообменных» сделок и взаимозачетов, переводом части счетов через дочерние структуры. За короткое время этот источник стал вторым по значению при формировании совокупных финансовых ресурсов большинства отраслей экономики, а для строительства и отдельных промышленных отраслей – доминирующим. Резкий рост прочих поступлений - в целом негативное явление. Оно свидетельствует об усилении непредсказуемости при формировании финансовых ресурсов, снижении точности расчета вероятных объемов, повышений риска «недополучения» финансовых средств.

Хронический недостаток финансовых ресурсов привел к переходу производственных предприятий на взаимное кредитование посредством выписываемых векселей, которые во многих случаях обходятся дешевле, чем кредиты коммерческих банков, и росту взаимных неплатежей.

Ухудшилось соотношение между кредиторской и дебиторской задолженностью. Просроченная кредиторская задолженность в целом по промышленности составляет половину задолженности этого типа. Такой высокий рост просроченной задолженности в экономическом плане означает столь же быстрое и значительное сокращение финансовых источников восстановления промышленности, ее отраслевой структуры, нормального воспроизводства. Основной причиной отрицательной динамики показателей соотношения дебиторской и кредиторской задолженности, а также устойчивой тенденции к росту просроченной задолженности в ее общей сумме, является физическое сокращение и разрушение основных производственных фондов, прекращение в большинстве случаев на только их расширенного воспроизводства, но и простого. В результате -резкое падение объемов производства, которое сопровождается сокращением собственных источников финансирования производства [6].

В результате осуществления воспроизводства в сокращающихся масштабах (в основном за счет заемных средств) увеличиваются затраты по обслуживанию долга, образующегося при банковском кредитовании. Все это свидетельствует о существенном расстройстве финансовой системы, обслуживающей процесс воспроизводства в промышленном комплексе.

Существует тенденция замещения задолженностью поставщикам и другим кредиторам части собственных оборотных средств предприятия и недостающих краткосрочных кредитов банка. Предприятия заинтересованы в замещении названных источников кредиторской задолженностью, пользование которой дешевле, чем банковскими кредитами.

8. Расчетная часть

 

Пусть x- количество крупных и средних организаций за год , y - сумма прибыли крупных и средних организаций за год, z - сумма убытка крупных и средних организаций за год. Занесем данные в таблицу 1.

 

Таблица 1. Исходные данные

Периоды времени	Количество крупных и средних организаций, единица, РФ, знание пок-ля за год Рос-ая соб-сть,	Сумма прибыли крупных и средних орг-ций, млн руб., знач-ие пок-ля за год	Сумма убытка крупных и средних орг-ций, млн руб., знач-ие пок-ля за год
	x	y	z
2002	137582	238493	113504
2003	140668	309008	135010
2004	144858	357579	472690
2005	144040	884868	161710
2007	136715	1357806	216553
2008	130572	1273415	350095
2010	108670	2778551	293113

 

Графический анализ исходных данных

 

График 1. Динамические ряды исходных данных

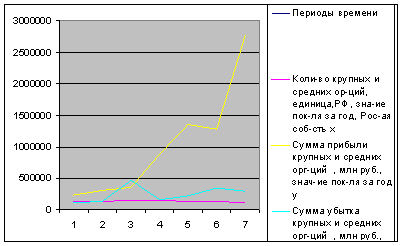
Графический анализ:

На основе графического анализа можно сделать вывод о том, что сумма прибыли крупных и средних организаций резко растут вплоть до 2010 года, а убытки крупных и средних организаций и число крупных и средних организаций постепенно падают, который на прямую зависит от прибыли и убытков организации.

 

Таблица 2. Исходные данные

Периоды времени	Показатель	Показатель	Показатель
	x	y	z
2002	137582	238493	113504
2003	140668	309008	135010
2004	144858	357579	472690
2005	144040	884868	161710
2007	136715	1357806	216553
2008	130572	1273415	350095
2010	108670	2778551	293113

Графический анализ исходных данных

 

График 2. Динамические ряды исходных данных

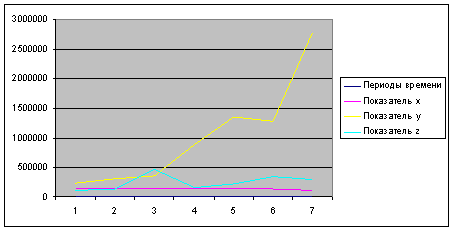
Вывод:

На графике видно, что прибыль организаций до конца 2007 растет равномерно. Затем наблюдается резкий рост прибыли организаций вплоть до конца 2010. Одновременно число крупных и средних организаций до конца 2005 года растут, а потом начинает снижаться и постепенно стабилизируется. Убытки крупных и средних организаций медленно растут до 2004 года, а потом резко снижаются и постепенно стабилизируется только к концу периода. Представляется, что имеется тесная обратная связь между прибылью и убытками организаций. Для проверки необходимо рассчитать линейные коэффициенты корреляции между числом организации , прибылью и убытками.

Расчет линейных коэффициентов корреляции

Рассмотрим расчеты с различными аналитическими показателями динамики. Для этого нужно построить вспомогательные таблицы и произвести расчеты.

Таблица 3. Показатели динамики х

Периоды	xt	Абсолютный прирост		Кофф-ты роста		Коэфф-ты прироста		Темпы роста		Темпы прироста
времени		Цепные	Базисные	Цепные	Базисные	Цепные	Базисные	Цепные	Базисные	Цепные	Базисные
2002	137582
2003	140668	3086	3086	1,0	1,0	0,0	0,0	0%	0%	- 100%	-100%
2004	144858	4190	7276	1,0	1,1	0,0	0,1	0%	10%	-100%	-110%
2005	144040	-818	-818	1,0	1,0	0,0	0,0	0%	0%	-100%	-100%
2007	136715	-7325	-7325	0,9	1,0	-0,1	0,0	-10%	0%	-110%	-100%
2008	130572	-6143	-13468	1,0	1,0	0,0	0,0	0%	0%	-100%	- 100%
2010	108670	-21902	-21902	0,8	0,8	-0,2	-0,2	-20%	-20%	-120%	-120 %
Средние значения:		-28912	-33151	5,8	5,9	-0,15	- 0.05	- 15%	-5%	-105%	- 105 %

 

Таблица 4. Показатели динамики - у

Периоды	yt	Абсолютный прирост		Кофф-ты роста		Коэфф-ты прироста		Темпы роста		Темпы прироста
времени		Цепные	Базисные	Цепные	Базисные	Цепные	Базисные	Цепные	Базисные	Цепные	Базисные
2002	238493
2003	309008	70515	70515	1,3	1,3	0.3	0.3	30%	30%	- 70%	- 70%
2004	357579	48571	119086	1,2	1,5	0.2	0,5	20%	50%	-80%	-50%
2005	884868	527289	646375	2,9	3,7	0.9	2,7	90%	270%	-10%	170%
2007	1357806	472938	1119313	1,5	5,7	0,5	4,7	50%	470%	-50%	370%
2008	1273415	-84391	1034922	0,9	5,3	-0,1	4,3	-10%	430%	-110%	210%
2010	2778551	1505136	2540058	2,2	12,0	0.2	11,0	20%	1100%	-80%	180%
Средние значения:		423343	921712	1.7	5	2	4	33%	391%	67%	135%

 

Таблица 5. Показатели динамики - z

Периоды	zt	Абсолютный прирост		Кофф-ты роста		Коэфф-ты прироста		Темпы роста		Темпы прироста
времени		Цепные	Базисные	Цепные	Базисные	Цепные	Базисные	Цепные	Базисные	Цепные	Базисные
2002	113504
2003	135010	21506	21506	1,2	1,2	0,2	0,2	20%	20%	- 80%	- 80 %
2004	472690	337680	359186	3,5	4,2	2,5	3,2	250%	320%	150%	220%
2005	161710	-310980	48206	0,3	1,4	-0,7	0,4	-70%	40%	-170%	-60%
2007	216553	54843	103049	1,3	1,9	0,3	0,9	30%	90%	-70%	- 10%
2008	350095	133542	236591	1,6	3,1	0,6	2,1	60%	210%	-40%	110%
2010	293113	-56982	179609	0,8	2,6	-0,2	1,6	-20%	160%	-80%	80%
Средние значения:		29934,833	158024,5	1,5	2,4	0,5	1,4	45%	140%	90 %	260%

 

Таблица 6. Средние показатели динамики

Сравнительный анализ средних показателей динамики для трех показателей
		показатель x		показатель y		показатель z
		Цепной	Базисный	Цепной	Базисный	Цепной	Базисный
Средний абсолютный прирост		-28912	-33151	423343	921712	29934,8	158024,5
Средний темп роста		- 15%	-5%	33%	391%	45%	140%
Средний темп прироста		-105%	- 105 %	67%	135%	90 %	260%

 

Вывод:

Наиболее высокими темпами растет показатель у ( прибыль оранизаций), а наиболее низкими темпами – показатель z – убытки организаций. В абсолютном выражении среднегодовые приросты доходов и расходов незначительно отличаются.

Расчет линейных коэффициентов корреляции

Вначале рассчитаем коэффициент корреляции между показателем x и показателем y. Построим вспомогательную таблицу 7 для расчета.

Таблица 7. Вспомогательная таблица для расчета коэффициента корреляции между показателем x и показателем y

Расчет линейного коэффициента корреляции между показателем x и показателем y
Периоды времени	Исходные данные		Вспомогательные расчеты
	Показатель	Показатель
	x	y
2002	137582	238493	146481	109254	21456683361	11936436516	16003635174
2003	140668	309008	149567	179769	22370287489	32316893361	26887510023
2004	144858	357579	153757	228340	23641215049	52139155600	35108873380
2005	144040	884868	152939	755629	23390337721	570975185641	115 565 143 631
2007	136715	1357806	145614	1228567	21203436996	1509376873489	178 896 555 138
2008	130572	1273415	139471	1144176	24912142609	1309138718976	159 579 370 896
2010	108670	2778551	117569	2649312	26183070169	7018854073344	311 476 962 528
	943105	7200320	1005398	6295047	163157173394	39627616732209	843518050770

Средние значения:

= - 8899; = 192239

Линейный коэффициент корреляции рассчитывается по формуле:

 

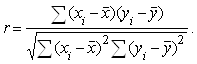
Таким образом

Вывод:

Коэффициент корреляции равен 0,25. Значит, связь между двумя показателями не тесная.

Теперь рассчитаем коэффициент корреляции между показателями у и z. Построим вспомогательную таблицу для расчета коэффициента корреляции между показателем y и показателем z.

 

Таблица 8 . Вспомогательная таблица для расчета коэффициента корреляции между показателем у и показателем z

Периоды времени	Расчет линейного коэффициента корреляции между показателем y и показателем z
	Исходные данные		Вспомогательные расчеты
	y	z
2002	238493	113504	109254	-74990	11936436516	5623545094,09	-8192990236,20
2003	309008	135010	179769	-53484	32316893361	2860570346,49	-9614819126,70
2004	357579	472690	228340	284196	52139155600	80767195898,49	64893246138,00
2005	884868	161710	755629	-26784	570975185641	717398726,49	-20238993824,70
2007	1357806	216553	1228567	28059	1509376873489	787290645,69	34471992882,90
2008	1273415	350095	1144176	161601	1309138718976	26114786240,49	184899642523,20
2010	2778551	293113	2649312	104619	7018854073344	10945072389,69	277167577334,40
	7200320	1742675	6295047	423215	10504737336927	127815859341,43	523385655690,90

Средние значения:

= 192239 , = 188494,3

r (y,z) =  ;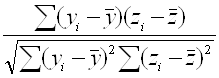

Таким образом

Вывод:

Коэффициент корреляции равен 0,23. Значит связь между двумя показателями не тесная.

В данном примере получилось, что связь y более тесная с показателем x, так как коэффициент корреляции 0,25 больше, чем 0,23.

Расчет параметров линейного и квадратического тренда для показателей x и y

Для расчета параметров уравнений линейного и квадратического тренда построим вспомогательную таблицу.

 

Таблица 9. Вспомогательная таблица для расчета параметров линейного и квадратического тренда

Исходные данные		Вспомогательные расчеты
Периоды времени		Условное обозначение времени			yt	yt2
	у	t	t2	t4
2002	238493	-3	9	81	-715479	2146437
2003	309008	-2	4	16	-618016	1236032
2004	357579	-1	1	1	-357579	357579
2005	884868	0	0	0	0	0
2007	1357806	1	1	1	1357806	1357806
2008	1273415	2	4	16	2546830	5093660
2010	2778551	3	9	81	8335653	25006959
S	7200320	0	28	196	10549215	35198473

Формулы для расчета параметров линейного тренда:

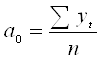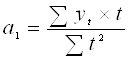Формулы для расчета параметров квадратичного тренда:

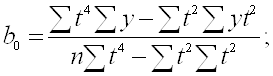Подставляя в эти формулы все суммы, рассчитанные в последней (итоговой) строке вспомогательной таблицы 4 (Σy =7200320 , Σt² = 28 Σt⁴=196, Σyt = 10549215, Σyt² = 35198473 ) , получаем следующие результаты:

Линейный тренд y		Квадратический тренд y
y^ = a0 + a1* t		y^^ = b0 + b1* t + b2*t2
a0 =	1507031	b0 =	142850,80
a1 =	53822,5	b1 =	53822,5
		b2 =	166659,2

 

Аналогичным образом рассчитаем параметры уравнений линейного и квадратического тренда для показателя x.

Таблица 10. Вспомогательная таблица для расчета параметров линейного и квадратического тренда

Периоды		Условное обозначение времени			x*t	x*t2
времени	x	t	t2	t4
2002	137582	-3	9	81	-412746	170359260516
2003	140668	-2	4	16	-281336	79149944896
2004	144858	-1	1	1	-144858	20983840164
2005	144040	0	0	0	0	0
2007	136715	1	1	1	136715	18690991225
2008	130572	2	4	16	261144	68196188736
2010	108670	3	9	81	326010	106282520100
∑	943105	0	28	196	-115071	463662745637

 

Линейный тренд x		Квадратический тренд x
х^ = a0 +a1* t		х^^ = b0 + b1* t + b*t2
a0 =	16438,71	b0 =	269458,57
a1 =	41073,96	b1 =	4109,67
		b2 =	1908420333761170

 

Чтобы выбрать, какое из уравнений тренда (линейное или квадратическое) лучше описывает исходный ряд данных, строится вспомогательная таблица для расчета так называемой ошибки аппроксимации, которая находится по формуле:

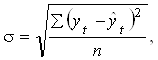
В этой формуле:

 –исходные значения уровня ряда;

– расчетные значения уровня ряда; т.е. f(t), где f(t) – уравнение соответствующей функции.

Таблица 11. Вспомогательная таблица для расчета ошибок аппроксимации

Периоды времени	Исходные данные		Расчетные данные
	y	t	y^	y^^	(y^ -y)2	(y^^ - y)2
2002	238493	-3	1345563,20	1481316,10	1225604427728	1544609257893,6
2003	309008	-2	1399385,70	701842,60	1188923528657	154319022957,2
2004	357579	-1	1453208,20	255687,50	1201003343893	10381877772,3
2005	884868	0	1507030,70	142850,80	387086425271	550589525095,8
2007	1357806	1	1560853,20	363332,50	41228165428	988977542202,3
2008	1273415	2	1614675,70	917132,60	116458865364	126937148549,8
2010	2778551	3	1668498,20	1804251,10	1232217218788	281786965063,2
S	7200320	0	10549214,90	5666413,20	5391921975129	3657601339534,1

 

Вид уравнения тренда	Ошибка
y^ = a0 + a1* t		8776528,60
y^^ = b0 + b1* t + b2*t2		6565569,50

 

Таблица 12. Расчет прогнозных значений по тренду

Вид уравнения тренда	Прогноз	Ошибка
y^ = a0 + a1* t	1776143,5	8776528,60
y^^ = b0 + b1* t + b2*t2	4578443,3	6565569,50

 

Вывод:

Из двух прогнозных значений более достоверным является y** = 6565569,5 так как ошибка аппроксимации для него меньше.

 

Таблица 16. Вспомогательная таблица для расчета ошибок аппроксимации

Периоды	Исходные данные		Расчетные данные
времени	x	t	2950075,2	x^^	(x^ - x)2	(x^^-х)2
2002	137582	-3	58273090,0	17175783004107700	59714336309	2950075,2
2003	140668	-2	3642068,0	7633681335305920	42591552807	58273090,0
2004	144858	-1	1572982,5	1908420334026520	28727961795	3642068,0
2005	144040	0	3642068,0	269459	16282089209	1572982,5
2007	136715	1	582773090,0	1908420334034740	6273009077	3642068,0
2008	130572	2	2950075,2	7633681335322360	10230638940	582773090,0
2010	108670	3	655803448,9	17175783004132300	960416668	2950075,2
∑	943105	0	16438,71	53435769347199000	164780004805	655803448,9

 

Ошибки аппроксимации и прогнозные значения для разных уравнений тренда
Вид уравнения тренда	Ошибка
x^ = a0 + a1* t	= 153427,51
x^^ = b0 + b1* t + b*t2	 9679,164
Вид уравнения тренда	Прогнозные значения
x^ = a0 +a1* t	x* = 221808,51
x^^ = b0 + b1* t + b*t2	x** = 1,9213572218

 

Вывод:

Из двух прогнозных значений более достоверным является x** = 1,9213572218 так как ошибка аппроксимации для него меньше.

Расчет параметров парной линейной регрессии

Для расчета параметров уравнения парной линейной регрессии y = a₀+a₁x составляется система нормальных уравнений:

na₀ + a₁Σx = Σy;

a₀Σx + a₁Σx² = Σxy.

Решают с помощью метода определителей. В результате получаются следующие формулы для расчета параметров уравнения парной линейной регрессии:

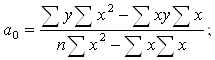
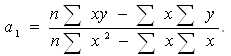
Построим вспомогательную таблицу. Обозначать их параметры разными буквами. Поэтому заменим a₀ на k₀ и a₁ на k₁.

Рассчитаем соответствующие суммы и подставим Σx, Σy, Σx², Σxy в формулы для расчета параметров парной линейной регрессии:

 

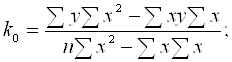
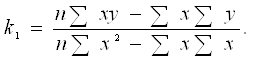
В результате расчетов получаем следующие значения параметров регрессии:

Параметры регрессии
k0 =	14004771,9
k1 =	63335,6

Ошибка аппроксимации
	3692,48

y	7761508,3

yx	7638683,7

R2 =	0,98

R² = 7638683,7 /7761508,3 = 0,98

Вывод: Ошибка аппроксимации равна 0,98 т.е. менее 10 % среднего значения y, равного 16438,71. Допустимо, если ошибка аппроксимации не превышает 10-15% от среднего значения результативного показателя. Индекс детерминации равен 0,98, то есть очень близок к 1. Значит, построенное уравнение регрессии является значимым, то есть описывает существенную зависимость между показателями.

Таблица 17. Вспомогательная таблица для расчета параметров уравнения парной линейной регрессии (y = k₀ + k₁*x )

Исходные данные		Вспомогательные расчеты				Расчет дисперсии фактических значений y		Расчет дисперсии расчетных значений yx
		Расчет параметров		Расчет ошибки()
x	y	x2	xy	yx=k0+k1*x	(y - yx)2
137582	238493	18928806724	32812343926	8727848794	761711815727542	-854159	729587597281	8726756142	76156272768567100000
140668	309008	19787486224	43467537344	8923302579	796198142756026	-783644	614097918736	8922209927	79605829988952006000
144858	357579	20983840164	51798178782	9188678911	844252489004537	-735073	540332315329	9187586259	84411741266933100000
144040	884868	20747521600	127456386720	9136870358	834662308643545	-207784	43174190656	9135777706	83462434284310800000
136715	1357806	18690991225	185632447290	8672936795	751962821537946	265154	70306643716	8671844143	75200880831811600000
130572	1273415	17049047184	166272343380	8283865958	686013392330279	180763	32675262169	8282773306	68604333638254900000
108670	2778551	11809168900	301945137170	6896688771	475259981172841	1685899	2842255438201	6895596119	47549245832230500000
943105	7200320	127996862021	68905323943135	59746163534	356874379758234	6107068	37296279556624	59745070882	3569473494707150000000

Расчет прогноза результирующего показателя y по регрессии

Рассчитанные параметры уравнений тренда для определения прогнозного значения показателя x. Были получены следующие результаты.

 

Ошибки аппроксимации и прогнозные значения для разных уравнений тренда
Вид уравнения тренда	Ошибка
x= a0 + a1* t	1 =	153427,51
x = b0 + b1* t + b2*t2	=	9679,164
Прогноз по линейному тренду	x* =	221808,51
Прогноз по квадратическому тренду	x**=	1,9213572218

Вывод:

Что более достоверным для показателя x является прогнозное значение по квадратическому тренду x**= 1,9213572218, так как для него ошибка аппроксимации меньше. Именно его и подставляем его в уравнение регрессии. Подставляем это число вместо x в уравнение: y = 14004771,9+ 63335,6x, получаем y***= 14125107.

Вывод (заключительный): Были рассчитаны тремя способами три разных прогнозных значения показателя y. По линейному тренду: y* =8776528,6; по квадратическому тренду y** = 6565569,5 и по уравнению регрессии y***=14125107.

Наиболее достоверным представляется прогнозное значение 6565569,5, рассчитанное по уравнению квадратического тренда, так как для данного уравнения ошибка аппроксимации наименьшая.

В целом следует сделать вывод о том, что от способа расчета зависит результат прогноза и что для получения более достоверного результата необходимо рассматривать различные варианты возможных видов математических функций, используемых для построения уравнений тренда.

Заключение

 

Финансы предприятий различных форм собственности, являясь основой единой финансовой системы страны, обслуживают процесс создания и распределения общественного продукта и национального дохода.

От состояния финансов предприятий зависит обеспеченность централизованных денежных фондов финансовыми ресурсами. При этом активное использование финансов предприятий в процессе производства и реализации продукции не исключает участия в этом процессе бюджета, банковского кредита, страхования.

В условиях рыночной экономики на основе хозяйственной и финансовой независимости предприятия осуществляют свою деятельность на началах коммерческого расчета, целью которого является обязательное получение прибыли. Они самостоятельно распределяют выручку от реализации продукции, формируют и используют фонды производственного и социального назначения, изыскивают необходимые им средства для расширения производства продукции, используя кредитные ресурсы и возможности финансового рынка. Развитие предпринимательской деятельности способствует расширению самостоятельности предприятий, освобождению их от мелочной опеки со стороны государства и вместе с тем повышению ответственности за фактические результаты работы.

 

Список использованных источников

 

1  Елисеева И.И., Юзбашев М.М. Общая теория статистики. М.: Финансы и статистика, 2006.

2  Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. М.: Финансы и статистика, 2009.

3  Салин В.Н., Шпаковская Е.П.Социально-экономическая статистика. М.: Финансы и статистика, 2005

4  Статистика/ Под ред. И.И. Елисеевой. М.: Финансы и статистика, 2010.

5  Статистика / Под ред. В.Г.Ионина. М.: Инфра-М, 2007.

6  Статистика финансов / Под ред. В.Н. Салина. М.: Финансы и статистика, 2010.

7  Теория статистики / Под ред. Р.А. Шмойловой. М.: Финансы и статистика, 2009.

8  Экономическая статистика / Под ред. Ю.Н. Иванова. М.: Инфра-М, 2006.