Навигация
Конечный хэш-адрес А(К) вычисляется по формуле А(К) = [M*F(K)], где М — размер хэш-таблицы, а скобки [] означают целую часть результата умножения
2. Конечный хэш-адрес А(К) вычисляется по формуле А(К) = [M*F(K)], где М — размер хэш-таблицы, а скобки [] означают целую часть результата умножения.
Удобно рассматривать эти две формулы вместе:
А(К) = М*(С*К) mod 1.
Кнут в качестве значения С рекомендует использовать «золотое сечение» — величину, равную ((л/5)-1)/2«0,6180339887. Значение F(K) можно формировать с помощью как команд сопроцессора, так и целочисленных команд. Команды сопроцессора вам хорошо известны и трудностей с реализацией формулы (2.4) не возникает. Интерес представляет реализация вычисления А(К) с помощью целочисленных команд. Правда, в отличие от реализации сопроцессором здесь все же Удобнее ограничиться условием, когда М является степенью 2. Тогда процесс вычисления с использованием целочисленных команд выглядит так:
Выполняем произведение С*К. Для этого величину «золотого сечения» С~0,6180339887 нужно интерпретировать как целочисленное значение,
обходимо стремиться к тому, чтобы появление 0 и 1 в выделяемых позициях было как можно более равновероятным. Здесь трудно дать рекомендации, просто нужно провести анализ как можно большего количества возможных ключей, разделив составляющие их байты на тетрады. Для формирования хэш-адреса нужно будет взять биты из тех тетрад (или полностью тетрады), значения в которых изменялись равномерно.
Метод квадрата
В литературе часто упоминается метод квадрата как один из первых методов генерации последовательностей псевдослучайных чисел. При этом он непременно подвергается критике за плохое качество генерируемых последовательностей. Но, как упомянуто выше, для процесса хеширования это не является недостатком. Более того, в ряде случаев это наиболее предпочтительный алгоритм вычисления значения хэш-функции. Суть метода проста: значение ключа возводится в квадрат, после чего берется необходимое количество средних битов результата. Возможны варианты — при различной длине ключа биты берутся с разных позиций. Для принятия решения об использовании метода квадрата для вычисления хэш-функции необходимо провести статистический анализ возможных значений ключей. Если они часто содержат большое количество нулевых битов, то это означает, что распределение значений битов в средней части квадрата ключа недостаточно равномерно. В этом случае использование метода квадрата неэффективно.
На этом мы закончим знакомство с методами хеширования, так как полное обсуждение этого вопроса не является предметом книги. Информацию об остальных методах (сегментации, перехода к новому основанию, алгебраического кодирования) можно получить из различных источников.
В ходе реализации хеширования с помощью методов деления и умножения возможные коллизии мы лишь обозначали без их обработки. Настало время разобраться с этим вопросом.
Обработка коллизий
Для обработки коллизий используются две группы методов:
· закрытые — в качестве резервных используются ячейки самой хэш-таблицы;
· открытые — для хранения элементов с одинаковыми хэш-адресами используется отдельная область памяти.
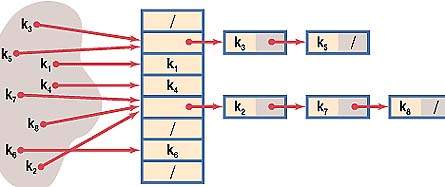
Видно, что эти группы методов разрешения коллизий соответствуют классификации алгоритмов хеширования — они тоже делятся на открытые и закрытые. Яркий пример открытых методов — метод цепочек, который сам по себе является самостоятельным методом хеширования. Он несложен, и мы рассмотрим его несколько позже.
Закрытые методы разрешения коллизий более сложные. Их основная идея — при возникновении коллизии попытаться отыскать в хэш-таблице свободную ячейку. Процедуру поиска свободной ячейки называют пробитом, или рехешированием (вторичным хешированием). При возникновении коллизии к первоначальному хэш-адресу А(К) добавляется некоторое значение р, и вычисляется выражение (2.5). Если новый хэш-адрес А(К) опять вызывает коллизию, то (2.5) вычисляется при р2, и так далее:
А(К) = (A(K)+Pi)mod М (I = 0..М). (2.5)
push ds popes
lea si .buf.len_in
mov cl .buf .lenjn
inccx :длину тоже нужно захватить
add di .lenjd repmovsb
jmp ml displ: :выводим идентификатор, вызвавший коллизию, на экран
рехэширование
;ищем место для идентификатора, вызвавшего коллизию в таблице, путем линейного рехэширования i nc bx mov ax.bx jmp m5
Квадратичное рехеширование
Процедура квадратичного рехеширования предполагает, что процесс поиска резервных ячеек производится с использованием некоторой квадратичной функции, например такой:
Pi = а,2+Ь,+с. (2.6)
Хотя значения а, Ь, с можно задавать любыми, велика вероятность быстрого зацикливания значений р(. Поэтому в качестве рекомендации опишем один из вариантов реализации процедуры квадратичного рехеширования, позволяющий осуществить перебор всех элементов хэш-таблицы [32]. Для этого значения в формуле (2.6) положим равными: а=1,Ь = с = 0. Размер таблицы желательно задавать равным простому числу, которое определяется формулой М = 4п+3, где п — целое число. Для вычисления значений р> используют одно из соотношений:
pi = (K+i2)modM. (2.7) Pi = [M+2K-(K+i2)modM]modM. (2.8)
где i = 1, 2, ..., (M-l)/2; К — первоначально вычисленный хэш-адрес.
Адреса, формируемые с использованием формулы (2.7), покрывают половину хэш-таблицы, а адреса, формируемые с использованием формулы (2.8), — вторую половину. Практически реализовать данный метод можно следующей процедурой.
1. Задание I = -М.
2. Вычисление хэш-адреса К одним из методов хэширования.
3. Если ячейка свободна или ключ элемента в ней совпадает с искомым ключом, то завершение процесса поиска. Иначе, 1:=1+1.
4. Вычисление h := (h+|i|)modM.
5. Если I < М, то переход к шагу 3. Иначе (если I > М), таблица полностью заполнена.
Программа та же, что приведена в методе линейного рехеширования, за исключением добавления одной команды для инициализации процесса рехеширования, самого фрагмента рехеширования и небольших изменений сегмента данных. могут являться методы, основанные на деревьях поиска, и т. п. Наибольший эффект от хеширования — при поиске по заданным идентификаторам или дескрипторам, что характерно для задач баз данных, обработки документов и т. д. Для задач, в которых поиск ведется сравнением или вычислением сложных логических функций, лучше использовать традиционные методы сортировки и поиска. Для того, чтобы совершить плавный переход к рассмотрению следующей структуры данных — спискам, вернемся еще раз к одной проблеме, связанной с массивами. Упоминалось, что среди массивов можно выделить массивы специального вида, которые называют разреженными. В этих массивах большинство элементов равны нулю. Отводить место для хранения всех элементов расточительно. Естественно, возникает желание сэкономить. Что для этого можно предпринять?
Техника обработки массивов предполагает, что все элементы расположены в соседних ячейках памяти. Для ряда приложений это недопустимое ограничение.
Обобщенно можно сказать, что все перечисленные выше структуры имеют общие свойства:
· постоянство структуры данных на всем протяжении ее существования;
· память для хранения отводится сразу всем элементам структуры и все элементы находятся в смежных ячейках памяти;
· отношения между элементами просты настолько, что можно исключить потребность в средствах хранения информации об их отношениях в какой бы то ни было форме.
Исходя из этих свойств, данные структуры данных и называют статическими. Снять подобные ограничения можно, используя другой тип данных — списки. Для них подобных ограничений не существует.
Преобразование ключей
Наиболее часто встречается операция поиска записи по идентифицирующему его полю - ключу. Поэтому файл, как правило, индексируется по ключевому полю. Поиск по ключу в общем виде может рассматриваться как преобразование значения ключевого поля в адрес записи в файле (или номер записи), то есть как функция вида f(key) -> m.
Очевидно, можно сформулировать обратную задачу: если некоторым образом подобрать функцию f(), то ее можно использовать для определения места в файле, куда следует поместить запись с ключом key. Основное требование к такой функции: она должна как можно более равномерно распределять записи с различными значениями ключа по файлу, то есть иметь "случайный" вид. Кроме того, необходимо каким-то образом решить проблему "коллизий", то есть попадания нескольких записей с различными ключами в один физический адрес (номер записи).
Функция f() называется распределяющей или рассеивающей функцией. Пример одной из таких функций: берется квадрат значения ключа, из него извлекаются n значащих цифр из середины, которые и дают значение номера записи в файле:
int Place1024(key) // Функция рассеивания для файла из
unsigned key; // 1024 записей и 16 разрядного
{ // ключа
unsigned long n,n1;
int m;
n = (unsigned long)key * key;
for (m=0, n1 = n; n1 !=0; m++, n1 >>= 1); // Подсчет количества значащих
if (m < 10) return(n); // битов в n
m = (m - 10) / 2; // m - количество битов по краям
return( (n >> m) & 0x3FF);
}
Известны два способа решения проблемы коллизий. В первом случае файл содержит область переполнения. Если функция f() вычисляет адрес записи в файле, а соответствующее место уже заполнено записью с другим значением ключа, то новая запись помещается в область переполнения. При этом возможны два варианта:
- записи в области переполнения не связаны между собой, и для поиска в ней используется последовательный просмотр всех записей;
- в области переполнения организуются списки записей, участвующих в коллизии: то есть запись в основной области является заголовком списка записей в области переполнения, куда попадают все записи, вступающие в коллизию.
В другом случае запись, вступившая в коллизию, помещается в некоторое свободное место файла, начиная от текущей занятой позиции. Возможные варианты поиска:
- первая свободная позиция, начиная от текущей;
- проверяются позиции, пропорциональные квадрату шага относительно текущей занятой, то есть m = ( f(key) + i * i ) mod n, где i - номер шага, n - размер таблицы. Такое размещение позволяет лучше "рассеивать" записи при коллизии.
Рассматриваемый метод обозначается терминами расстановка или хеширование (от hash - смешивать, перемалывать).
Одним из существенных недостатков метода является необходимость заранее резервировать файл для размещения записей с номерами от 0 до m - в диапазоне возможных значений функции рассеивания. Кроме того, при заполнении файла увеличивается количество коллизий и эффективность метода падает. Если же количество записей возрастает настолько, что файл необходимо расширять, то это связано с изменением функции рассеивания и перераспределением (перезаписью) уже имеющихся записей в соответствии с новой функцией.
ГЛАВА 2. ПРАКТИЧЕСКАЯ ЧАСТЬ
Похожие работы
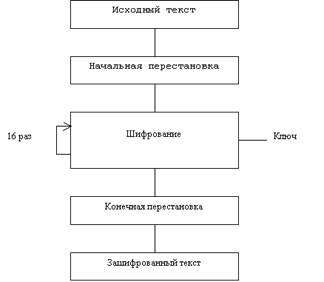
... ; - длина обрабатываемого блока; - сложность аппаратной/программной реализации; - сложность преобразования. В данном курсовом проекте предлагается программная реализация алгоритма шифровании DES (режим ЕСВ). 1. Описание алгоритма Стандарт шифрования данных DES опубликован в 1977 г. Национальным бюро стандартом США. Стандарт DES предназначен для защиты от несанкционированного доступа к ...
... и исправления ошибок в текстах на естественных языках (назовем их автокорректорами - АК, хотя терминология ещё не сложилась) получают все большее распространение. Они используются, в частности, в пакетах WINWORD и EXCEL для проверки орфографии текстовой информации. Говоря точнее, АК производят автоматически лишь обнаружение ошибок, а собственно коррекция ведется обычно при участии человека. 1. ...
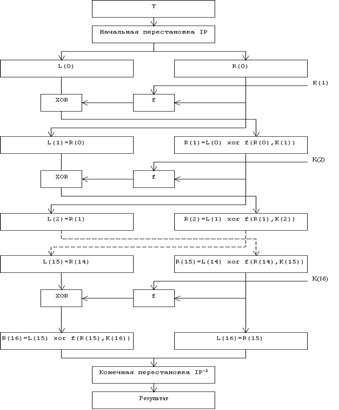
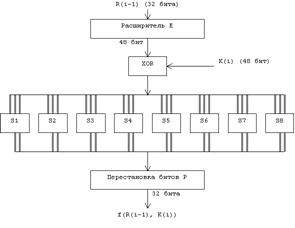
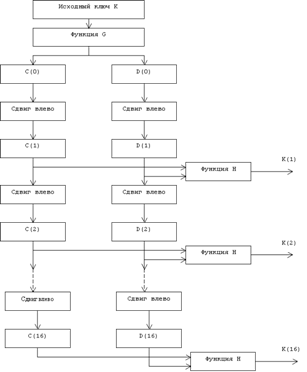
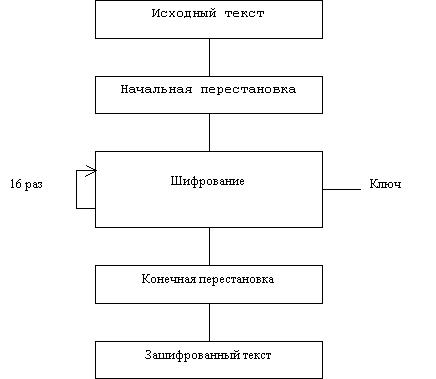
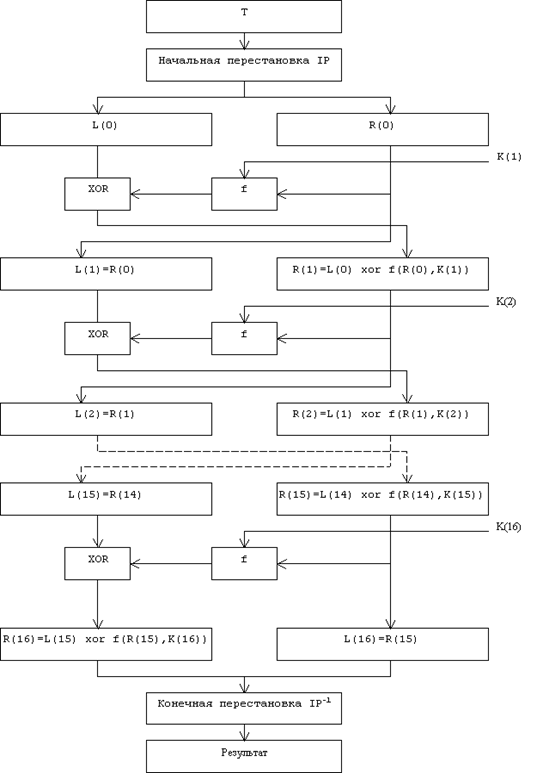
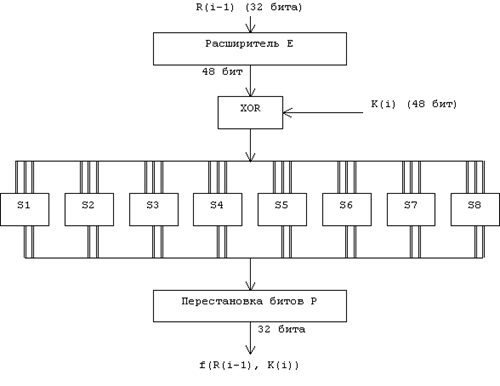
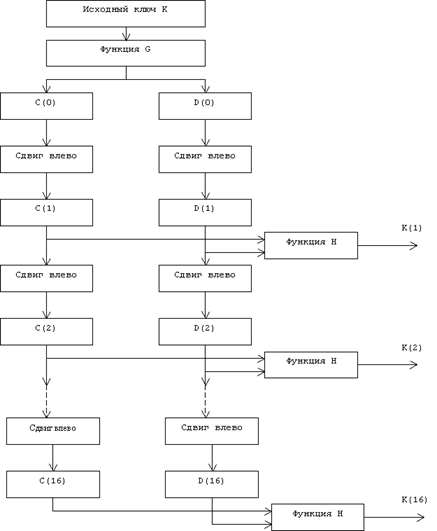
... виде. Все перестановки и коды в таблицах подобраны разработчиками таким образом, чтобы максимально затруднить процесс расшифровки путем подбора ключа. Структура алгоритма DES приведена на рис.2. Рис.2. Структура алгоритма шифрования DES Пусть из файла считан очередной 8-байтовый блок T, который преобразуется с помощью матрицы начальной перестановки IP (табл.1) следующим образом: бит 58 ...
... примененного алгоритма), так и возможность априорного задания требуемой криптостойкости. Криптостойкость данной системы определяется длиной ключа, криптостойкостью отдельных функциональных элементов алгоритма криптографических преобразований, а также количеством таких преобразований. Шифр взбивания Результат шифрования можно ощутимо улучшить, если вместо перестановки использовать линейное ...
0 комментариев