Навигация
Вставка элемента в в-дерево
2.1. Вставка элемента в в-дерево
Рассмотрим структуру узла B-дерева.
В каждом узле мы будем хранить не более NumberOfItems записей. Также нам надо будет хранить текущее количество записей в узле. Для удобства возврата назад к корню дерева будем запоминать для каждого узла указатель на его узел-предок.
Type
PBTreeNode = ^TBTreeNode;
TBTreeNode = record {узел дерева}
Count: Integer;
PreviousNode: PBTreeNode;
Items: array[0..NumberOfItems+1] of record
Value: ItemType;
NextNode: PBTreeNode;
end;
end;
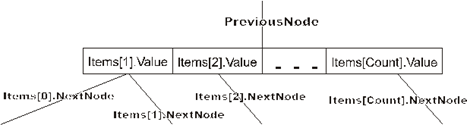
У элемента Items[0] будет использоваться только поле NextNode. Дополнительный элемент Items[NumberOfItems+1] предназначен для обработки переполнения, о чем будет рассказано ниже, где будет обсуждаться алгоритм добавления элемента в B-дерево.
Поскольку дерево упорядочено, то Items[1].Value<Items[2].Value<…< Items[Count].Value. Указатель Items[i].NextNode указывает на поддерево элементов, больших Items[i].Value и меньших Items[i+1].Value. Понятно, что указатель Items[0].NextNode будет указывать на поддерево элементов, меньших Items[1].Value, а указатель Items[Count].NextNode – на поддерево элементов, больших Items[Count].Value.
Само дерево можно задать просто указанием корневой вершины. Естественно, что у такой вершины PreviousNode будет равен nil.
Type
TBTree = TBTreeNode;
Прежде чем рассматривать алгоритмы, соберем воедино все требования к B-дереву:
1. каждый узел имеет не более NumberOfItems сыновей;
2. каждый узел, кроме корня, имеет не менее NumberOfItems/2 сыновей;
3. корень, если он не лист, имеет не менее 2-х сыновей;
4. все листья расположены на одном уровне (дерево сбалансировано);
5. нелистовой узел с k сыновьями содержит не менее k-1 ключ.
Из всего вышесказанного можно сразу сформулировать алгоритм поиска элемента в B-дереве.
Поиск элемента в B-дереве
Поиск будем начинать с корневого узла. Если искомый элемент присутствует в загруженной странице поиска, то завершаем поиск с положительным ответом, иначе загружаем следующую страницу поиска, и так до тех пор, когда либо найдем искомый элемент, либо не окажется «следующей страницы поиска» (пришли в лист B-дерева).
Посмотрим на примере, как это будет работать. Пусть мы имеем такое дерево (в наших примерах мы будем разбирать небольшие деревья, хотя в реальности B-деревья применяются при работе с большими массивами информации):
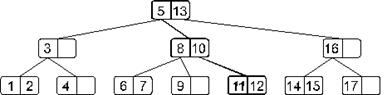
Будем искать элемент 11. Сначала загрузим корневой узел. Эта страница поиска содержит элементы 5 и 13. Наш искомый элемент больше 5, но меньше 13. Значит, идем по ссылке, идущей от элемента 5. Загружаем следующую страницу поиска (с элементами 8 и 10). Эта страница тоже не содержит искомого элемента. Замечаем, что 11 больше 10 – следовательно, двигаемся по ссылке, идущей от элемента 10. Загружаем соответствующую страницу поиска (с элементами 11 и 12), в которой и находим искомый элемент. Итак, в этом примере, чтобы найти элемент, нам понадобилось три раза обратиться к внешней памяти для чтения очередной страницы.
Если бы в нашем примере мы искали, допустим, элемент 18, то, просмотрев 3 страницы поиска (последней была бы страница с элементом 17), мы бы обнаружили, что от элемента 17 нет ссылки на поддерево с элементами большими 17, и пришли бы к выводу, что элемента 18 в дереве нет.
Теперь точно сформулируем алгоритм поиска элемента Item в B-дереве, предположив, что дерево хранится в переменной BTree, а функция LookFor возвращает номер первого большего или равного элемента узла (фактически производит поиск в узле).
function BTree.Exist(Item: ItemType): Boolean;
Var
CurrentNode: PBTreeNode;
Position: Integer;
begin
Exist := False;
CurrentNode := @BTree;
Repeat
Position := LookFor(CurrentNode, Item);
if (CurrentNode.Count>=Position)and
(CurrentNode.Items[Position].Value=Item) then
begin
Exist := True;
Exit;
end;
if CurrentNode.Items[Position-1].NextNode=nil then
Break
else
CurrentNode := CurrentNode.Items[Position-1].NextNode;
until False;
end;
Здесь мы пользуемся тем, что, если ключ лежит между Items[i].Value и Items[i+1].Value, то во внутреннюю память надо подкачать страницу поиска, на которую указывает Items[i].NextNode.
Заметим, что для ускорения поиска ключа внутри страницы поиска (функция LookFor), можно воспользоваться дихотомическим поиском, который описан ранее в главе, где разбирались способы хранения множества элементов в последовательном массиве.
Учитывая то, что время обработки страницы поиска есть величина постоянная, пропорциональная размеру страницы, сложность алгоритма поиска в B-дереве будет T(h), где h – глубина дерева.
Добавление элемента в B-дерево
Для того чтобы наше дерево можно было считать эффективной структурой данных для хранения множества значений, необходимо, чтобы каждый узел заполнился хотя бы наполовину. Дерево строится снизу. Это означает, что любой новый элемент добавляется в листовой узел. Если при этом произойдет переполнение (на этот случай в каждом узле зарезервирован лишний элемент), то есть число элементов в узле превысит NumberOfItems, то надо будет разделить узел на два узла, и вынести средний элемент на верхний уровень. Может случиться, что при этой операции на верхнем уровне тоже получится переполнение, что вызовет еще одно деление. В худшем случае эта волна докатится до корня дерева.
В общем виде алгоритм добавления элемента Item в B-дерево можно описать следующей последовательностью действий:
1. Поиск листового узла Node, в который следует произвести добавление элемента Item.
2. Добавление элемента Item в узел Node.
3. Если Node содержит больше, чем NumberOfItems элементов (произошло переполнение), то
o делим Node на две части, не включая в них средний элемент;
o Item=средний элемент Node;
o Node=Node.PreviousNode;
o Переходим к пункту 2.
Заметим, что при обработке переполнения надо отдельно обработать случай, когда Node – корень, так как в этом случае Node.PreviousNode=nil.
Посмотрим, как это будет работать, на примере.
Возьмем нарисованное ниже дерево и добавим в него элемент 13.
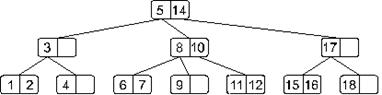
Двигаясь от корня, найдем узел, в который следует добавить искомый элемент. Таким узлом в нашем случае окажется узел, содержащий элементы 11 и 12. Добавим. В результате наше дерево примет такой вид:
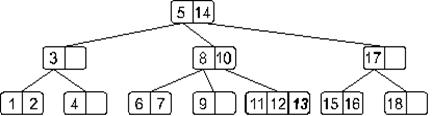
Понятно, что мы получили переполнение. При его обработке узел, содержащий элементы 11, 12 и 13 разделится на две части: узел с элементом 11 и узел с элементом 13, – а средний элемент 12 будет вынесен на верхний уровень. Дерево примет такой вид:
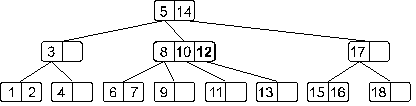
Мы опять получили переполнение, при обработке которого узел, содержащий элементы 8, 10 и 12 разделится на два узла: узел с элементом 8 и узел с элементом 12, – а средний элемент 10 будет вынесен на верхний уровень. И теперь дерево примет такой вид:
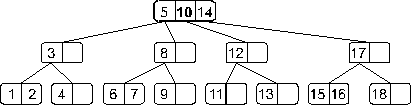
Теперь мы получили переполнение в корне дерева. Как мы оговаривали ранее этот случай надо обработать отдельно. Это связано с тем, что здесь мы должны будем создать новый корень, в который во время деления будет вынесен средний элемент:
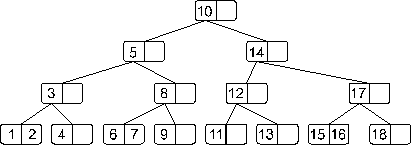
Теперь полученное дерево не имеет переполнения.
В этом случае, как и при поиске, время обработки страницы поиска есть величина постоянная, пропорциональная размеру страницы, а значит, сложность алгоритма добавления в B-дерево будет также T(h), где h – глубина дерева.
Итак, как мы заметили с самого начала, у B-деревьев есть своя сфера применения: хранение настолько больших массивов информации, что их невозможно целиком разместить в выделяемой оперативной памяти, но требуется обеспечить быстрый доступ к ним.
В таких случаях B-деревья являются хорошим средством программно ускорить доступ к данным.
Ярким примером практического применения B-деревьев является файловая система NTFS, где B-деревья применяются для ускорения поиска имен в каталогах. Если сравнить скорость поиска в этой файловой системе и в обычной FAT на примере поиска на жестком диске большого объема или в каталоге, содержащем очень много файлов, то можно будет констатировать превосходство NTFS. А ведь поиск файла в каталоге всегда предшествует запуску программы или открытию документа.
B-деревья обладают прекрасным качеством: во всех трех операциях над данными (поиск/удаление/добавление) они обеспечивают сложность порядка T(h), где h – глубина дерева. Это значит, что чем больше узлов в дереве и чем сильнее дерево ветвится, тем меньшую часть узлов надо будет просмотреть, чтобы найти нужный элемент. Попробуем оценить T(h).
Число элементов в узле есть величина вероятностная с постоянным математическим ожиданием MK. Математическое ожидание числа узлов равно:
![]() ,
,
где n – число элементов, хранимых в B-дереве. Это дает сложность T(h)=T(log(n)), а это очень хороший результат.
Поскольку узлы могут заполняться не полностью (иметь менее NumberOfItems элементов), то можно говорить о коэффициенте использования памяти. Эндрю Яо доказал, что среднее число узлов после случайных вставок при больших n и NumberOfItems составит N/(m*ln(2))+F(n/m2), так что память будет использоваться в среднем на ln(2)*100%.
В отличие от сбалансированных деревьев B-деревья растут не вниз, а вверх. Поэтому (и из-за разной структуры узлов) алгоритмы включения/удаления принципиально различны, хотя цель их в обоих случаях одна – поддерживать сбалансированность дерева.
Идея внешнего поиска с использованием техники B-деревьев была предложена в 1970 году Р.Бэйером и Э.Мак-Крэйтом и независимо от них примерно в то же время М.Кауфманом. Естественно, что за это время было предложено ряд усовершенствований B-деревьев, связанных с увеличением коэффициента использования памяти и уменьшением общего количества расщеплений.
Одно из таких усовершенствований было предложено Р.Бэйером и Э.Мак-Крэйтом и заключалось в следующем. Если узел дерева переполнен, то прежде чем расщеплять этот узел, следует посмотреть, нельзя ли «перелить» часть элементов соседям слева и справа. При использовании такой методики уменьшается общее количество расщеплений и увеличивается коэффициент использования памяти.
| program PTree; {$APPTYPE CONSOLE} type TInfo = Byte; PItem = ^Item; Item = record Key: TInfo; Left, Right: PItem; end; TTree = class private Root: PItem; public constructor Create; procedure Add(Key: TInfo); procedure Del(Key: TInfo); procedure View; procedure Exist(Key: TInfo); destructor Destroy; override; end; //--------------------------------------------------------- constructor TTree.Create; begin Root := nil; end; //--------------------------------------------------------- procedure TTree.Add(Key: TInfo); procedure IniTree(var P: PItem; X: TInfo); //создание корня дерева begin New(P); P^.Key :=X; P^.Left := nil; P^.Right := nil; end; procedure InLeft (var P: PItem; X : TInfo); //добавление узла слева var R : PItem; begin New(R); R^.Key := X; R^.Left := nil; R^.Right := nil; P^.Left := R; end; procedure InRight (var P: PItem; X : TInfo); //добавить узел справа var R : PItem; begin New(R); R^.Key := X; R^.Left := nil; R^.Right := nil; P^.Right := R; end; procedure Tree_Add (P: PItem; X : TInfo); var OK: Boolean; begin OK := false; while not OK do begin if X > P^.Key then //посмотреть направо if P^.Right <> nil //правый узел не nil then P := P^.Right //обход справа else begin //правый узел - лист и надо добавить к нему элемент InRight (P, X); //и конец OK := true; end else //посмотреть налево if P^.Left <> nil //левый узел не nil then P := P^.Left //обход слева else begin //левый узел -лист и надо добавить к нему элемент InLeft(P, X); //и конец OK := true end; end; //цикла while end; begin if Root = nil then IniTree(Root, Key) else Tree_Add(Root, Key); end; //------------------------------------------------------------- procedure TTree.Del(Key: TInfo); procedure Delete (var P: PItem; X: TInfo); var Q: PItem; procedure Del(var R: PItem); //процедура удаляет узел имеющий двух потомков, заменяя его на самый правый //узел левого поддерева begin if R^.Right <> nil then //обойти дерево справа Del(R^.Right) else begin //дошли до самого правого узла //заменить этим узлом удаляемыйQ^.Key := R^.Key; Q := R; R := R^.Left; end; end; //Del begin //Delete if P <> nil then //искать удаляемый узел if X < P^.Key then Delete(P^.Left, X) else if X > P^.Key then Delete(P^.Right, X) | //искать в правом поддереве else begin //узел найден, надо его удалить //сохранить ссылку на удаленный узел Q := P; if Q^.Right = nil then //справа nil //и ссылку на узел надо заменить ссылкой на этого потомка P := Q^.Left else if Q^.Left = nil then //слева nil //и ссылку на узел надо заменить ссылкой на этого потомка P := P^.Right else //узел имеет двух потомков Del(Q^.Left); Dispose(Q); end else WriteLn('Такого элемента в дереве нет'); end; begin Delete(Root, Key); end; //------------------------------------------------------------- procedure TTree.View; procedure PrintTree(R: PItem; L: Byte); var i: Byte; begin if R <> nil then begin PrintTree(R^.Right, L + 3); for i := 1 to L do Write(' '); WriteLn(R^.Key); PrintTree(R^.Left, L + 3); end; end; begin PrintTree (Root, 1); end; //------------------------------------------------------------- procedure TTree.Exist(Key: TInfo); procedure Search(var P: PItem; X: TInfo); begin if P = nil then begin WriteLn('Такого элемента нет'); end else if X > P^. Key then //ищется в правом поддереве Search (P^. Right, X) else if X < P^. Key then Search (P^. Left, X) else WriteLn('Есть такой элемент'); end; begin Search(Root, Key); end; //------------------------------------------------------------- destructor TTree.Destroy; procedure Node_Dispose(P: PItem); //Удаление узла и всех его потомков в дереве begin if P <> nil then begin if P^.Left <> nil then Node_Dispose (P^.Left); if P^.Right <> nil then Node_Dispose (P^.Right); Dispose(P); end; end; begin Node_Dispose(Root); end; //------------------------------------------------------------- procedure InputKey(S: String; var Key: TInfo); begin WriteLn(S); ReadLn(Key); end; var Tree: TTree; N: Byte; Key: TInfo; begin Tree := TTree.Create; repeat WriteLn('1-Добавить элемент в дерево'); WriteLn('2-Вывести узлы дерева'); WriteLn('3-Проверить существование узла'); WriteLn('4-Выход'); ReadLn(n); with Tree do begin case N of 1: begin InputKey('Введите значение добавляемого элемента', Key); Add(Key); end; 2: View; 3: begin InputKey('Введите элемент, существование которого вы хотите проверить', Key); Exist(Key); end; end; end; until N=4; Tree.Destroy; end. |
2.2 ОБРАБОТКА ТЕКСТОВЫХ ФАЙЛОВ
Разработать блок-схему алгоритма и составить программу обработки текстовых данных, хранящихся в произвольном файле на магнитном диске. Вид обработки данных: подсчитать количество слов, которые содержат определённое количество согласных.
Привожу исходный текст программы: Program file; uses crt; label fin; Const mn=['б','в','д','ж','з','к','л','м','н','п','р','с','т','ф','х','ц','ч','ш','щ']; Var f3:text; i,j,ch,sl:integer; name:string; s:char; wrd :string; dbase:string; Begin clrScr; writeln('vvedite imya faila'); readln(name); assign(f3,name); reset(f3); s:=' '; sl:=0; ch:=0; while not eof(f3) do begin readln(f3,wrd); i:=1; While i<=length(wrd) do begin if wrd[i]<>' ' then sl:=sl+1; while (wrd[i]<>' ') and (i<=length(wrd)) do inc(i); inc(i) end; end; close(f3); reset(f3); while not eof(f3) do begin while not eoln(f3) do begin read(f3,s); if (s in mn) then ch:=ch+1; end; end; wrd:='c:\den.txt'; assign(f3,wrd); {$I-} append(f3); {$I+} if IOResult <> 0 then begin {$I-} rewrite(f3); {$I+} if IOResult <> 0 then begin writeln('ERROR!'); goto fin; end; end; write(f3,' kol-vo slov --',sl,' kol-vo soglasnih --',ch,''); writeln('chislo slov: ',sl,' chiso soglasnih: ',ch); close(f3); fin: readkey; End.Приложение к выполненным программам
1. Обработка текстовых файлов
¦ Ввод данных ¦
¦ Запись в файл ¦
¦ Считывание файла ¦
¦ Обработка данных ¦
¦ Вывод результата ¦
+------ Выход ------+
Ввод данных:
Я хочу есть и спать, ещё я бы поиграл в комп. Запись в файл TEXT.pasВывод результата:
chislo slov: 11 chiso soglasnih: 17 Содержание выходного файла DEN.txt: kol-vo slov --11 kol-vo soglasnih --17 2. Вставка элемента в В-дерево 1-Dobavit element v derevo 2-Vivesti uzli dereva 3-Provtrit sushestvovanie uzla 4-vihod 1 Vvedite znacgenie dobavlayemogo elementa 33 1-Dobavit element v derevo 2-Vivesti uzli dereva 3-Provtrit sushestvovanie uzla 4-vihod 1 Vvedite znacgenie dobavlayemogo elementa 22 1-Dobavit element v derevo 2-Vivesti uzli dereva 3-Provtrit sushestvovanie uzla 4-vihod 1 Vvedite znacgenie dobavlayemogo elementa 44 1-Dobavit element v derevo 2-Vivesti uzli dereva 3-Provtrit sushestvovanie uzla 4-vihod 1 Vvedite znacgenie dobavlayemogo elementa 11 1-Dobavit element v derevo 2-Vivesti uzli dereva 3-Provtrit sushestvovanie uzla 4-vihod 2 44 33 22 11 1-Dobavit element v derevo 2-Vivesti uzli dereva 3-Provtrit sushestvovanie uzla 4-vihodЗАКЛЮЧЕНИЕ Была выполнена курсовая работа по предмету «Структуры и алгоритмы компьютерной обработки данных» на тему «Алгоритмы преобразования ключей (расстановка)». В данной курсовой работе рассмотрены теоретические вопросы и выполнены практические задания, которые соответствуют выданному заданию. В данной курсовой работе можно выделить 3 основных части, которые соответствуют следующим статусам: 1. Теоретическая часть; 2. Теоретическая + практическая часть; 3. Практическая часть; В курсовой представлена вся необходимая информация по данной курсовой, использована как научная литература, так и возможности всемирной сети Internet. Выполнены практические задания, и использованием знаний и умений программировать на алгоритмических языках высокого уровня Turbo Pascal, Borland Delphi.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Hellerman H. Digital Computer System Principles. McGraw-Hill, 1967.
2. Ершов А.П. Избранные труды. Новосибирск: ВО «Наука», 1994.
3. Кнут Д. Искусство программирования, т.3. М.: Вильямс, 2000.
4. Peterson W.W. Addressing for Random-Access Storage // IBM Journal of Research and Development. 1957. V.1, N2. Р.130—146.
5. Morris R. Scatter Storage Techniques // Communications of the ACM, 1968. V.11, N1. Р.38—44.
6. Ахо А., Хопкрофт Дж., Ульман Дж. Структуры данных и алгоритмы. М.: Вильямс, 2000.
7. Чмора А. Современная прикладная криптография. М.: Гелиос АРВ, 2001.
8. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. М.: МЦНМО, 2001.
9. Вирт Н. Алгоритмы + структуры данных = программы. М.: Мир, 1985.
10. Керниган Б., Пайк Р. Практика программирования. СПб.: Невский диалект, 2001.
11. Шень А. Программирование: теоремы и задачи. М.: МЦНМО, 1995.
Похожие работы
... ; - длина обрабатываемого блока; - сложность аппаратной/программной реализации; - сложность преобразования. В данном курсовом проекте предлагается программная реализация алгоритма шифровании DES (режим ЕСВ). 1. Описание алгоритма Стандарт шифрования данных DES опубликован в 1977 г. Национальным бюро стандартом США. Стандарт DES предназначен для защиты от несанкционированного доступа к ...
... и исправления ошибок в текстах на естественных языках (назовем их автокорректорами - АК, хотя терминология ещё не сложилась) получают все большее распространение. Они используются, в частности, в пакетах WINWORD и EXCEL для проверки орфографии текстовой информации. Говоря точнее, АК производят автоматически лишь обнаружение ошибок, а собственно коррекция ведется обычно при участии человека. 1. ...
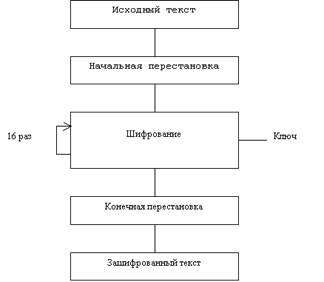
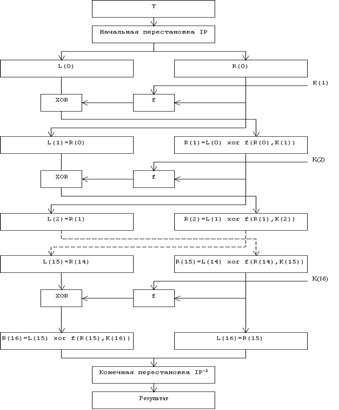
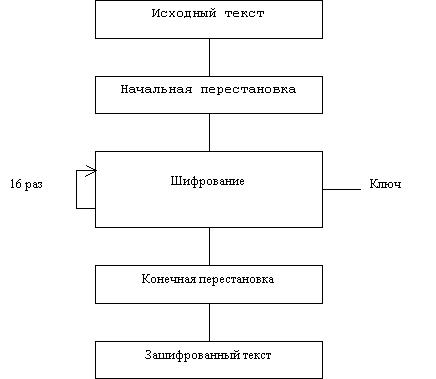
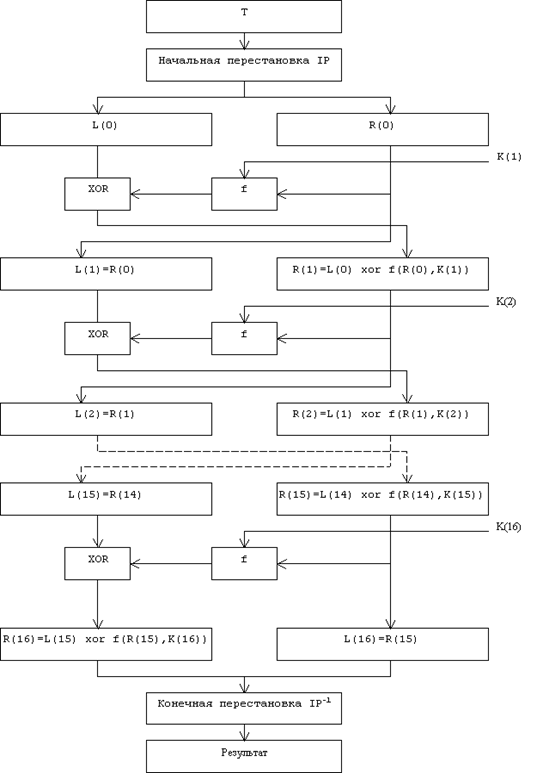
... виде. Все перестановки и коды в таблицах подобраны разработчиками таким образом, чтобы максимально затруднить процесс расшифровки путем подбора ключа. Структура алгоритма DES приведена на рис.2. Рис.2. Структура алгоритма шифрования DES Пусть из файла считан очередной 8-байтовый блок T, который преобразуется с помощью матрицы начальной перестановки IP (табл.1) следующим образом: бит 58 ...
... примененного алгоритма), так и возможность априорного задания требуемой криптостойкости. Криптостойкость данной системы определяется длиной ключа, криптостойкостью отдельных функциональных элементов алгоритма криптографических преобразований, а также количеством таких преобразований. Шифр взбивания Результат шифрования можно ощутимо улучшить, если вместо перестановки использовать линейное ...
0 комментариев