Моделирование связи социально-экономических явлений

2.  Моделирование связи социально-экономических явлений

 

После априорного анализа исходных статистических данных следует моделирование связи социально-экономических явлений.

Моделирование предполагает:

·  отбор факторных признаков

·  построение модели связи и оценка ее существенности

·  интерпретацию модели связи (уравнения регрессии)

2.1  Отбор факторных признаков

 

Признаки, обуславливающие изменение других, связанных с ними признаков, называют факторными, или просто факторами. Признаки, изменяющиеся под воздействием факторных признаков, называют результативными.

Для выявления наличия связи между признаками, ее характера и направления в статистике используются методы приведения параллельных данных, аналитических группировок, графический, корреляционный и регрессионный.

Метод приведения параллельных данных основан на сопоставлении двух или нескольких рядов статистических величин.

В таблице 2.1 предприятия ранжированы по величине себестоимости проданных товаров, продукции, работ, услуг.

Таблица 2.1

Показатели доходов и расходов по обычным видам деятельности предприятий, ранжированные по величине себестоимости, тыс. руб.

Номер предприятия	Себестоимость проданных товаров, продукции, работ, услуг	Выручка от продажи товаров, продукции, работ, услуг	Коммерческие и управленческие расходы
1	2	3	4
1	8109	21903	13697
13	14860	33702	19372
5	24126	35475	11042
2	46692	76581	28889
6	50729	78417	26413
9	66579	82279	20556
3	71378	116565	43834
4	83304	139317	54508
14	90233	139722	42770
7	102338	149687	44716
10	108977	158161	37419
15	155565	221771	60932
11	157775	225792	56192
17	163552	176430	11529
8	218436	287056	65048
12	222019	297921	73114
18	223176	244843	22200
16	284117	374199	81486
19	360237	395322	32614
Итого	2452202	3255143	746331

Отсюда видно, что с увеличением себестоимости увеличивается и выручка от продаж, хотя в отдельных случаях такая зависимость не наблюдается. Это говорит о возможном наличии прямой корреляционной связи. Связь между величиной коммерческих и управленческих расходов и другими признаками не наблюдается.

Статистическую связь между двумя признаками можно изобразить графически. За x обозначается факторный признак, в данном случае себестоимость. За у обозначается результативный признак – выручка.

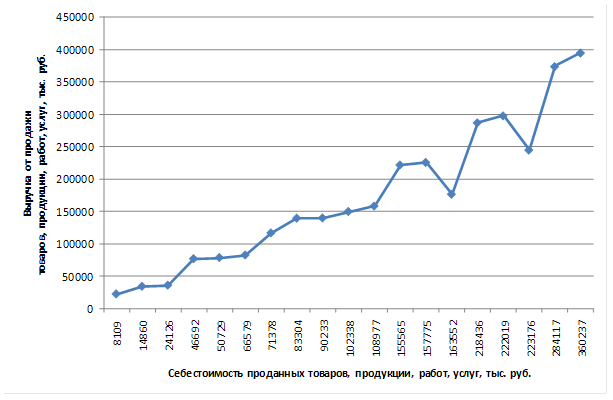Рис. 2.1 Зависимость величины выручки от себестоимости

Линия, соединенная точками, называется «ломаная регрессии». Число точек ломаной регрессии соответствует числу предприятий.

Точнее определить наличие и тесноту связи можно с помощью различных показателей. Зная показатели, можно выявить те факторы, которые в данных конкретных условиях являются решающими и главным образом воздействуют на формирование величины результативного признака.

К показателям тесноты связи относится линейный коэффициент корреляции.

В статистической теории разработаны и на практике применяются различные модификации формул расчета данного коэффициента:

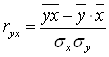 ,(2.1)

где x – факторный признак;

y – результативный признак.

Выполнив несложные преобразования можно получить следующую формулу (2.2):

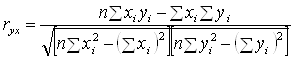.(2.2)

При пользовании этой формулой отпадает необходимость вычислять отклонения индивидуальных значений признаков от средней величины, что исключает ошибку в расчетах при округлении средних величин.

Линейный коэффициент корреляции может принимать любые значения в пределах от -1 до +1. Чем ближе коэффициент корреляции по абсолютной величине к 1, тем теснее связь между признаками. Знак при линейном коэффициенте корреляции указывает на направление связи - прямой зависимости соответствует знак плюс, обратной – знак минус.

На основе данных таблицы 1.1(2.1), с помощью формулы (2.2), было определено два коэффициента корреляции.

Во-первых, коэффициент корреляции, показывающий степень тесноты связи между себестоимостью и выручкой от продаж.

Пусть x₁ – величина себестоимости проданных товаров, продукции, работ, услуг. Тогда, y – величина выручки от продажи товаров, продукции, работ, услуг.

Отсюда r = 0,98, связь является прямой и очень сильной. Что значит, с увеличением себестоимости увеличивается и выручка.

Во-вторых, рассчитан коэффициент корреляции, показывающий степень тесноты связи между расходами и выручкой от продаж. В данной ситуации x₂ – величина коммерческих и управленческих расходов, а y – величина выручки от продажи товаров, продукции, работ, услуг.

Коэффициент корреляции равен 0,66, что говорит о прямой связи между признаками.

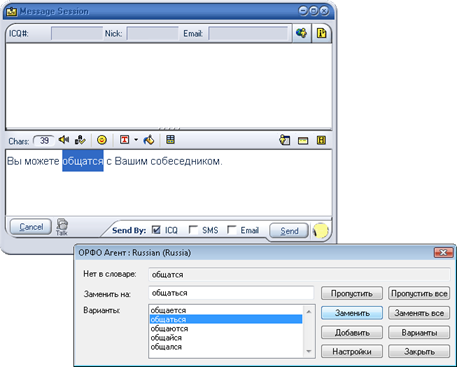
Тесноту связи между факторными признаками можно также рассчитать по формуле (2.1), заменяя результативный признак на факторный:

.

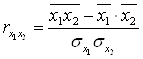(2.3)

= 0,51.

Полученная величина свидетельствует о наличии прямой зависимости между значениями себестоимости и расходов.

Для наглядности была построена матрица парных коэффициентов корреляции:

y – величина выручки от продажи товаров, продукции, работ, услуг;

x₁ – величина себестоимости проданных товаров, продукции, работ, услуг;

x₂ – величина коммерческих и управленческих расходов.

Таблица 2.2

Матрица парных коэффициентов корреляции

	y	x1	x2
y	1,00	0,98	0,66
x1	0,98	1,00	0,51
x2	0,66	0,51	1,00

Матрица парных коэффициентов корреляции показывает, что результативный показатель наиболее тесно связан с показателем x₁.

Так как существует линейная связь между результативным и двумя факторными признаками, а также между парой факторных признаков, то имеет смысл рассчитать множественный коэффициент корреляции.

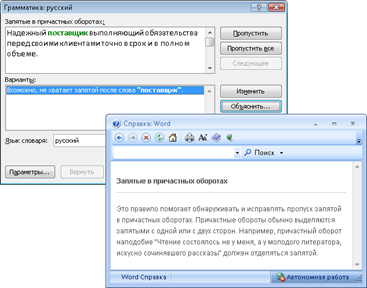
В данной работе множественный коэффициент корреляции был вычислен по формуле (2.4):

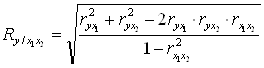.(2.4)

= 0,99.

Связь между показателями сильная, факторы x₁ и x₂ практически полностью обуславливают величину y.

При построении модели связи, или регрессии, может возникнуть проблема мультиколлинеарности (наличие сильной корреляции между независимыми переменными, входящими в уравнение регрессии). Мультиколлинеарность существенно искажает результаты исследования.

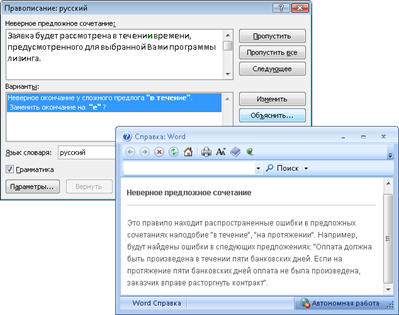
Наиболее распространенный метод выявления коллинеарности основан на анализе парных коэффициентов корреляции. Он состоит в том, что две или несколько переменных признаются коллинеарными (мультиколлинеарными), если парные коэффициенты корреляции больше определенной величины. На практике наиболее часто считают, что два аргумента коллинеарны, если парный коэффициент корреляции между ними по абсолютной величине больше 0,8.

В данном примере парный коэффициент корреляции не превышает величины 0,8 (= 0,51), что говорит об отсутствии явления мультиколлинеарности.