Навигация
Физическая трактовка процессов интерполяции сигналов
2. Физическая трактовка процессов интерполяции сигналов
Основное математическое соотношение интерполяционной обработки:
![]() , (8)
, (8)
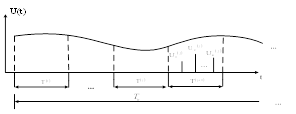
можно проиллюстрировать следующим образом (рисунок 3).
В качестве интерполяционной функции в этом примере используется функция ![]() . Интервалы интерполяции
. Интервалы интерполяции![]() и обработки
и обработки ![]() должны последовательно сдвигаться по времени. Операцию интерполяции можно выполнить с помощью линейного фильтра с импульсной характеристикой вида:
должны последовательно сдвигаться по времени. Операцию интерполяции можно выполнить с помощью линейного фильтра с импульсной характеристикой вида:
![]() . (9)
. (9)
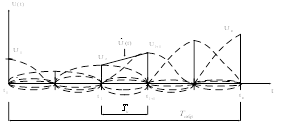
Рисунок 3
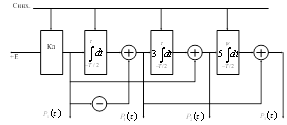
Для доказательства этого утверждения обозначим сигнал на входе и выходе линейного фильтра через ![]() и
и ![]() (рисунок 4):
(рисунок 4):
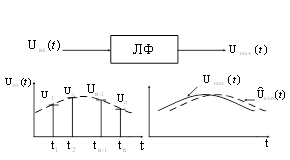
Рисунок 4
Представим сигнал на входе линейного фильтра в виде последовательности кратковременных импульсов, площадь которых равна соответствующим выборкам
![]() . (10)
. (10)
Из свойств линейных систем следует, что сигнал на выходе равен:
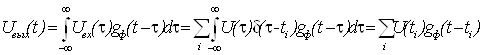 (11)
(11)
Выражение (11) получается с учетом фильтрующего свойства δ-функции. Если импульсная характеристика линейного фильтра ![]() удовлетворяет выражению (9), то соотношение (11) переходит в формулу для интерполяционной обработки:
удовлетворяет выражению (9), то соотношение (11) переходит в формулу для интерполяционной обработки:
![]() . (12)
. (12)
Идеальное восстановление функции на выходе линейного фильтра невозможно, т.к.:
- отклик на выходе линейного фильтра не может появиться раньше соответствующей выборки на входе;
- число выборок не равно бесконечности;
- АЧХ фильтра отличается от идеальной.
3. Задачи идеальной интерполяции
В общем случае формула интерполяции имеет вид:
![]() , (13)
, (13)
![]() - оценка значения i-ой выборки,
- оценка значения i-ой выборки, ![]() - восстановленный первичный сигнал,
- восстановленный первичный сигнал,
![]() .
.
Интерполяция возможна в том случае, если в сигнале имеются корреляционные связи. Может быть поставлена задача оптимального выбора вида функции ![]() , при которой ошибка интерполяции минимальна.
, при которой ошибка интерполяции минимальна.
Рассмотрим задачу идеальной интерполяции сигнала при предположении, что ![]() , т.е. отсутствуют внешние шумы и ошибки системы.
, т.е. отсутствуют внешние шумы и ошибки системы.
Пусть непрерывный первичный сигнал описывается корреляционной
функцией ![]() . Требуется определить форму интерполирующей функции, обеспечивающей при заданных значениях коэффициента корреляции минимум СКО
. Требуется определить форму интерполирующей функции, обеспечивающей при заданных значениях коэффициента корреляции минимум СКО
![]() . (14)
. (14)
Можно показать, что в этом случае оптимальная интерполирующая функция имеет вид:
![]() , (15)
, (15)
где ![]() - весовые коэффициенты, однозначно связанные со значениями коэффициентов корреляции в точках
- весовые коэффициенты, однозначно связанные со значениями коэффициентов корреляции в точках ![]() ,
, ![]() .
.
Т.о., оптимальная интерполирующая функция может быть определена как взвешенная сумма функций времени равных корреляционной функции первичного сигнала. Как следствие этой теории может бать доказана следующая теорема:
Если на интервале интерполяции ![]() корреляционная функция
корреляционная функция ![]() и ее взвешенная сумма хорошо аппроксимируются полиномом, то использование этого приближения обеспечит среднеквадратическое приближение близкое к идеальному. Т.е. требуется хорошая аппроксимация не всей корреляционной функции, а только ее части, приходящейся на интервал интерполяции (рисунок 5).
и ее взвешенная сумма хорошо аппроксимируются полиномом, то использование этого приближения обеспечит среднеквадратическое приближение близкое к идеальному. Т.е. требуется хорошая аппроксимация не всей корреляционной функции, а только ее части, приходящейся на интервал интерполяции (рисунок 5).
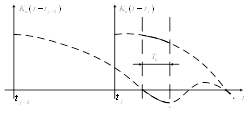
Рисунок 5
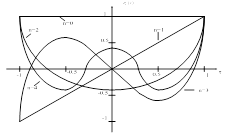
Чем меньше ![]() , тем точнее возможна аппроксимация в виде многочлена и тем проще могут быть аппроксимирующие полиномы. Проиллюстрируем эту теорему для сигнала с прямоугольным спектром (рисунок 6):
, тем точнее возможна аппроксимация в виде многочлена и тем проще могут быть аппроксимирующие полиномы. Проиллюстрируем эту теорему для сигнала с прямоугольным спектром (рисунок 6):

Рисунок 6
Известно, что в этом случае в соответствии с теоремой
В.А. Котельникова возможно разложение первичного сигнала в ряд:
![]() , (16)
, (16)
где ![]() - частота опроса. В точках
- частота опроса. В точках ![]()
![]() интерполирующая функция равна:
интерполирующая функция равна:
![]() . (17)
. (17)
Сопоставим этот результат с выражением для идеальной интерполирующей функции:
![]() . (18)
. (18)
Чтобы эти формулы совпали, необходимо чтобы при ![]() , а в случае
, а в случае ![]()
![]()
![]() , т. е. чтобы корреляционная функция имела вид:
, т. е. чтобы корреляционная функция имела вид:
![]() . (19)
. (19)
Такой функцией корреляции обладает сигнал с прямоугольным спектром, а условие ![]() при
при ![]() приводит к требованию, чтобы частота опроса
приводит к требованию, чтобы частота опроса ![]() .
.
Это соотношение не может быть использовано на практике по следующим причинам:![]()
Похожие работы
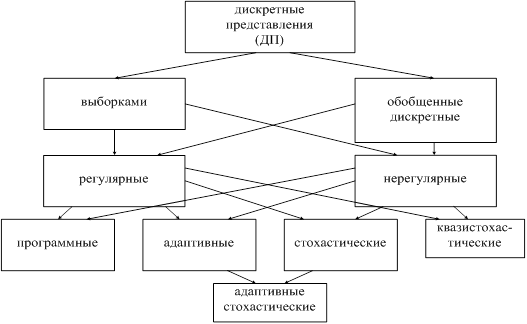
... аналоговых выборок, которые формируются через определенные интервалы времени (используются АИМ, ШИМ, ВИМ). Дискретно-квантованное представление отличается от дискретно-аналогового тем, что выборки формируются в цифровой форме. При обобщенном дискретном представлении координаты сообщения представляют собой коэффициенты некоторого ряда, это позволяет сократить количество координат, т.е. объем выб
... представления – результат соединения адаптивных и стохастических представлений, при которых одна группа характеристик изменяется стохастически, а другая адаптируется к измененному сообщению. 3. Рациональное представление информации При ракетно-космических исследованиях наметилась постоянная тенденция к росту космических измерений и регистрации на борту летательного объекта информации. На ...
... разработаны технические устройства, в частности компьютеры, которые специально предназначены для автоматической обработки информации. 2. Кодирование информации. Способы кодирования. Кодирование информации В процессе преобразования информации из одной формы представления (знаковой системы) в другую осуществляется кодирование. Средством кодирования служит таблица соответствия, которая ...
... функций в виде зависимости их значений от определенных аргументов Δвремени, линейной или пространственной координаты и т.п.) при анализе и обработке данных широко используется математическое описание сигналов по аргументам, обратным аргументам динамического представления. Так, например, для времени обратным аргументом является частота. Возможность такого описания определяется тем, что любой ...




0 комментариев