Навигация
Сигнала с идеальным прямоугольным спектром не существует
16090
знаков
1
таблица
15
изображений
1. Сигнала с идеальным прямоугольным спектром не существует.
2. Число выборок 
.
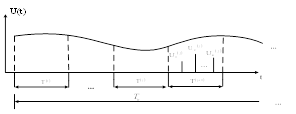
На практике при представлении регулярными выборками частота опроса выбирается исходя из соотношения
æ
, (20)
где определяется формой спектра сигнала, а æ – коэффициент запаса, зависящий от вида интерполирующих полиномов и требуемых значений показателя верности.
4. Интерполяция алгебраическими полиномами
цифровой кодирование алгебраический полином
Как было показано выше, для первичных сигналов с разными корреляционными функциями необходимо использовать разные интерполирующие функции. Такой подход не приемлем для практики, т.к. требует выполнения большого объема предварительных работ для определения вида интерполирующих функций. Для преодоления этих затруднений возможны два пути:
1. Использование для группы сигналов с близкими корреляционными функциями интерполирующей функции одного вида.
2. Применение в качестве интерполирующих функций хорошо программируемых функций с выбором частоты опроса, обеспечивающих во всех случаях требуемую верность.
Второй путь наиболее прост, но приводит к завышенным частотам опроса и, следовательно, к увеличению загрузки радиолинии. Наиболее рациональным является комбинированное использование обоих путей.
Во многих случаях в качестве интерполирующих путей используются алгебраические полиномы низких степеней, в частности полиномы Лагранжа. Интерполирующая функция по Лагранжу записывается в следующем виде:
(21)
где 
- символ произведения, в котором отсутствуют сомножители при 
. Нетрудно убедиться, что 
при 
и 
при 
.
При интерполяции по Лагранжу требуется определенным образом выбрать интервал обработки 
.
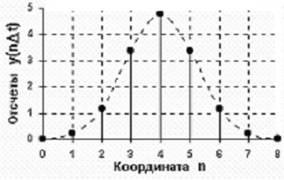
1) Число точек опроса n четное (рисунок 7).
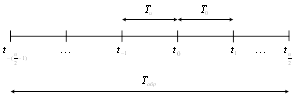
Рисунок 7
2) Число точек опроса n нечетное (рисунок 8).
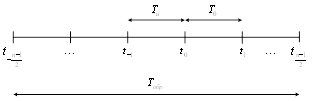
Рисунок 8
Запишем момент времени, в котором ищется интерполяционная оценка в виде
, (22)
где 
- точка отсчета, 
- период опроса, 
- безразмерное время, которое может непрерывно изменяться в пределах
, при 
(23)
, при 
, 
(24)
На практике интерполяция по Лагранжу используется при n = 1, 2, 3:
1. Ступенчатая интерполяция (полиномы нулевой степени) (рисунок 9).
В этом случае n = 1 и для интерполяции используется лишь одна выборка
, 
, 
и 
.
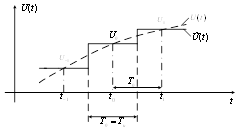
Рисунок 9
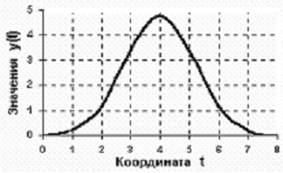
2. Линейная интерполяция (полиномы первой степени) (рисунок 10).
При этом 
, 
, 
и интерполирующие функции имеют вид
, 
.
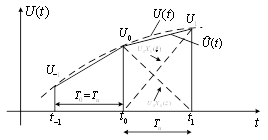
Рисунок 10
Похожие работы
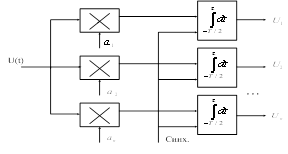
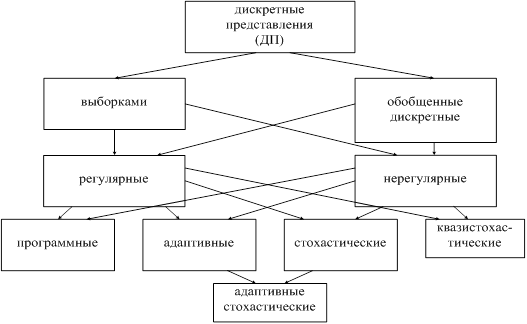
... аналоговых выборок, которые формируются через определенные интервалы времени (используются АИМ, ШИМ, ВИМ). Дискретно-квантованное представление отличается от дискретно-аналогового тем, что выборки формируются в цифровой форме. При обобщенном дискретном представлении координаты сообщения представляют собой коэффициенты некоторого ряда, это позволяет сократить количество координат, т.е. объем выб
... представления – результат соединения адаптивных и стохастических представлений, при которых одна группа характеристик изменяется стохастически, а другая адаптируется к измененному сообщению. 3. Рациональное представление информации При ракетно-космических исследованиях наметилась постоянная тенденция к росту космических измерений и регистрации на борту летательного объекта информации. На ...
... разработаны технические устройства, в частности компьютеры, которые специально предназначены для автоматической обработки информации. 2. Кодирование информации. Способы кодирования. Кодирование информации В процессе преобразования информации из одной формы представления (знаковой системы) в другую осуществляется кодирование. Средством кодирования служит таблица соответствия, которая ...
... функций в виде зависимости их значений от определенных аргументов Δвремени, линейной или пространственной координаты и т.п.) при анализе и обработке данных широко используется математическое описание сигналов по аргументам, обратным аргументам динамического представления. Так, например, для времени обратным аргументом является частота. Возможность такого описания определяется тем, что любой ...
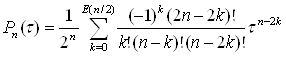
0 комментариев