Навигация
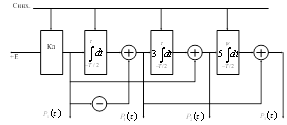
Квадратичная интерполяция (квадратичная интерполяция) (рисунок 11)
3. Квадратичная интерполяция (квадратичная интерполяция) (рисунок 11).
При этом ![]() ,
, ![]() ,
, ![]() и интерполирующие функции имеют вид
и интерполирующие функции имеют вид
![]() ,
, ![]() ,
, ![]() .
.

Рисунок 11
Можно показать, что верхние оценки относительных ошибок в этом случае равны
![]() ,
, ![]() ,
, ![]() ,
,
где ![]() - граничная частота спектра сигнала,
- граничная частота спектра сигнала, ![]() - частота опроса.
- частота опроса.
При ![]() и
и ![]() частота опроса
частота опроса
![]() ,
, ![]() ,
, ![]() .
.
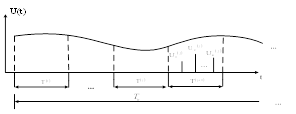
При восстановлении функции по отсчетам обычно получается плавная кривая, поэтому, можно для практических расчетов выбрать частоту опроса по формуле ![]() .
.
5. Определение частоты опроса
Определим частоту опроса первичного сигнала при среднем квадратическом приближении алгебраическими полиномами. Используем показатель верности оценки ![]() в форме интегральной средней квадратической ошибки
в форме интегральной средней квадратической ошибки
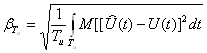 . (26)
. (26)
Более удобно использовать приведенный показатель верности:
![]() . (27)
. (27)
Применим эту формулу для определения частоты опроса четырех моделей первичного сигнала:
Модель 1. Сигнал с ограниченным равномерным спектром (рисунок 12).

Рисунок 12
Применяя косинус преобразование Фурье от ![]() , получим функцию корреляции этого сигнала:
, получим функцию корреляции этого сигнала:
![]() . (28)
. (28)
Модель 2. Сигнал с треугольным спектром (рисунок 13).
![]() ,
, ![]() .
.
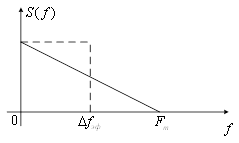
Рисунок 13
Эффективная ширина спектра в этом случае имеет вид
![]() ,
,
а функция корреляции равна
![]() . (29)
. (29)
Модель 3. Сигнал марковского типа (рисунок 14).
Энергетический спектр этого сигнала описывается соотношением
 ,
,
а функция корреляции равна
![]() . ( 30)
. ( 30)
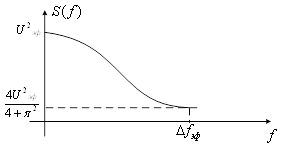
Рисунок 14
Модель 4. Сигнал с колокольным спектром (рисунок 15).
Энергетический спектр этого сигнала описывается соотношением
![]() ,
,
где
![]() ,
,
а функция корреляции равна
![]() . (31)
. (31)

Рисунок 15
Эти модели охватывают значительную часть практически используемых сигналов и являются стационарными случайными процессами. Применяя для этих моделей интерполяцию по Лагранжу при ![]() получим следующие формулы (таблица 1) для расчета величины æ =
получим следующие формулы (таблица 1) для расчета величины æ = ![]() .
.
В случае модели 1 и идеальной интерполяции, т.е. при опросе по В.А. Котельникову, æ = 1. Формулы, приведенные в таблице используются для определения частоты опроса ![]() = æ
= æ![]() .
.
Таблица 1
| Модель | æ = | ||
| 1 | n = 1 | n = 2 | n = 3 |
|
|
|
| |
| 2 |
|
|
|
| 3 |
|
|
|
| 4 |
|
|
|
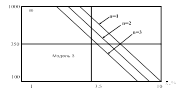
Построим графики зависимости æ от показателя верности ![]() для различных моделей сигналов (рисунки 16, 17).
для различных моделей сигналов (рисунки 16, 17).
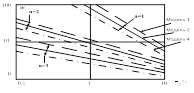
Рисунок 16
![]()
Рисунок 17
Заключение
Для всех моделей, за исключением третьей, интерполяция полиномами более высокого порядка позволяет уменьшить частоту опроса при той же верности.
1. При переходе от линейной интерполяции к квадратичной, уменьшение частоты опроса ![]() не столь значительно, как при переходе от ступенчатой интерполяции к линейной.
не столь значительно, как при переходе от ступенчатой интерполяции к линейной.
2. Увеличивать степень полинома целесообразно только при увеличении требований к точности интерполяции.
3. Для третьей модели переход от линейной модуляции к квадратичной нецелесообразен, что объясняется свойствами марковских сигналов.
4. При интерполяции алгебраическими полиномами первичного сигнала коэффициент корреляции между соседними выборками равен 0,85 – 0,995. Это приводит к неэффективному использованию пропускной способности канала передачи информации.
5. Для определения частоты опроса необходимо располагать:
- спектральными характеристиками первичного сигнала, т.е. полосой ![]() по уровню 0,99 энергии сигнала;
по уровню 0,99 энергии сигнала;
- точностными характеристиками, т.е. показателем верности ![]() %;
%;
- задать алгоритм обработки, т.е. тип интерполирующего полинома.
Список литературы:
1. Радиотехнические методы передачи информации: Учебное пособие для вузов / В.А. Борисов, В.В. Калмыков, Я.М. Ковальчук и др.; Под ред. В.В. Калмыкова. М.: Радио и связь. 1990. 304с.
2. Системы радиосвязи: Учебник для вузов / Н.И. Калашников, Э.И. Крупицкий, И.Л. Дороднов, В.И. Носов; Под ред. Н.И. Калашникова. М.: Радио и связь. 1988. 352с.
3. Тепляков И.М., Рощин Б.В., Фомин А.И., Вейцель В.А. Радиосистемы передачи информации: Учебное пособие для вузов / М.: Радио и связь. 1982. 264с.
4. Кириллов С.Н., Стукалов Д.Н. Цифровые системы обработки речевых сигналов. Учебное пособие. Рязань. РГРТА, 1995. 80с.
5. Кириллов С.Н., Бакке А.В. Оптимизация сигналов в радиотехнических системах. Учебное пособие. Рязань. РГРТА, 1997. 80с.
6. Кириллов С.Н., Шелудяков А.С. Методы спектральной обработки речевых сигналов. Учебное пособие. Рязань. РГРТА, 1997. 80с.
Похожие работы
... аналоговых выборок, которые формируются через определенные интервалы времени (используются АИМ, ШИМ, ВИМ). Дискретно-квантованное представление отличается от дискретно-аналогового тем, что выборки формируются в цифровой форме. При обобщенном дискретном представлении координаты сообщения представляют собой коэффициенты некоторого ряда, это позволяет сократить количество координат, т.е. объем выб
... представления – результат соединения адаптивных и стохастических представлений, при которых одна группа характеристик изменяется стохастически, а другая адаптируется к измененному сообщению. 3. Рациональное представление информации При ракетно-космических исследованиях наметилась постоянная тенденция к росту космических измерений и регистрации на борту летательного объекта информации. На ...
... разработаны технические устройства, в частности компьютеры, которые специально предназначены для автоматической обработки информации. 2. Кодирование информации. Способы кодирования. Кодирование информации В процессе преобразования информации из одной формы представления (знаковой системы) в другую осуществляется кодирование. Средством кодирования служит таблица соответствия, которая ...
... функций в виде зависимости их значений от определенных аргументов Δвремени, линейной или пространственной координаты и т.п.) при анализе и обработке данных широко используется математическое описание сигналов по аргументам, обратным аргументам динамического представления. Так, например, для времени обратным аргументом является частота. Возможность такого описания определяется тем, что любой ...
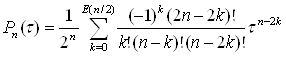




0 комментариев