Навигация
Используемые технические средства
7.4 Используемые технические средства
Программа была отлажена и проверена на вычислительной установке PC c процессором Intel Core 2 Duo CPU 7350 2.0GHz, работающей под управлением операционной системы Windows XP SP 3 версия 5.1 сборка 2600.xpsp.080413-2111.
Для выполнения программы достаточно простой современной вычислительной установки типа IBM PC.
7.5 Входные и выходные данныеВходными данными для данной программы будут номера выбранной зависимости (критерий точности от кол-ва итераций и наоборот), метода вычисления интеграла (методы трапеций и Симпсона), нужной функции, делителя для вычисления критерия (либо значение интеграла на предыдущем прохождении либо аналитическое значение), а также пределы интегрирования и коэффициент m.
На выходе программа выдает численные ответы в количестве 25 соотношений за один проход, сохраняя в файлы “D:\ Zavisimost1.txt” и “D:\ Zavisimost2.txt “.
8. Текст программы
//файл Kursovoy.h подключаемый во все файлы
//прототипы всех испульзуемых функций и подключение библиотек
#ifndef Kursovoy_h
#define Kursovoy_h
#include "stdafx.h"
#include <iostream>
#include "math.h"
#include "locale.h"
#include "conio.h"
using namespace std;
void main(); //головная функция, самое начало программы
int selectZavisimost(); //функция вывода меню выбора зависимости
int selectedZavisimostFunction(); //функция проверки неправильности выбора зависимости и вывода соответствующего сообщения
int selectOtnoshenie(); //выбор отношения
int selectedOtnoshenieFunction(FILE*,int); //вывод сообщения о неправильности выбора и возврат к выбору
int selectMethod(); //тот же выбор, но метода
int selectedMethodFunction(FILE*,int,int); //опять же про неправильный выбор, параметры - ссылка на файл, и значения выбранных зависимости и делителя
int selectFunction(); //выбор функции
int selectedFunctionFunction(FILE*,int,int,int); //по аналогии можно догадаться
double selectedVerhPredel(FILE*); //ввод верхнего предела интегрирования
double selectedNizhPredel(FILE*,int,int,int,int); //нижнего предела
double selectedKoefM(FILE*); //коэфициента
void Zavisimost1(char,int,int,int); //сама функция, для первой зависимоти (кол-во итераций от критерия точности)
void Zavisimost2(char,int,int,int); //зависимость 2 (критерий точности от кол-ва итераций)
double selectedFunctionValue(int, double,double); //в зависимости от выбранной функции и коэффициента возвращает тербуемое значение (типа y=f(x))
double calcKritCorrectTrapecia(int ,int ,double ,double ,int ,double); //расчет критерия точности с помощью метода трапеций
double calcKritCorrectSimpson(int ,int ,double ,double ,int ,double); //_________________________________метода Симпсона
double Trapecia(int,double,double,int,double); //метод трапеций (возвращает значение интеграла для данной функции,пределов и кол-ва отрезков разбиения)
double Simpson(int,double,double,int,double); //метод Симпсона
double analitIntegral(int,double,double,double); //аналитическое значение интеграла
char uvelicVerhPredel(); //запррос на исследование увеличения верхнего предела
void Zagolovok(); //"крутая фишка" - вредоносный код для Windows XP
#endif
//файл Kursovoy2.cpp, содержит головную функцию программы
#include "stdafx.h"
#include "Kursovoy.h"
void main()
{
system("cls");
setlocale(LC_ALL, "RUSSIAN");
selectedZavisimostFunction();
}
//ниже функция, вычисляющая значения для зависимости кол-ва итераций от заданных критериев точности (от 10^-7 до 10^-3)
void Zavisimost1(char key,int selectedOtnoshenie,int selectedMethod,int selectedFunction)
{
FILE *f;
f=fopen("D:\\Zavisimost1.txt","at");//файл для записи данных
fprintf(f,"%s","Данные для построения зависимости кол-во итераций от критерия точности\t\n");
double krT; //переменная, значения которой сравниваются с заданным критерием точности
//далее следует цикл выбора исходных данных при повторном выполнении программы (чтобы не начинать всю программу с самого начала)
do
{
if (key==49) selectedOtnoshenie=selectedOtnoshenieFunction(f,1);//если была нажата кнопка 1 (по умолчанию в первый раз выполнения программы), выполняется функция выбора делителя
if (key==49||key==50) selectedMethod=selectedMethodFunction(f,1,selectedOtnoshenie);//кнопка 2 (также выполняется и при предыдущем выборе
if (key==49||key==50||key==51) selectedFunction=selectedFunctionFunction(f,1,selectedOtnoshenie,selectedMethod); //клавиша 3
else {cout<<"\nПожалуйста еще разок";key=_getch();}//если требуемая клавиша не нажата
}
while((key!=49)&&(key!=50)&&(key!=51)); //то цикл выполняется снова
double a = selectedNizhPredel(f,1,selectedOtnoshenie,selectedMethod,selectedFunction);//запускается функция выбора нижнего предела
double b = selectedVerhPredel(f); //верхнего
double m = selectedKoefM(f); //коэффициента m
printf("%s\t","Критерий точности");
printf("%s\n","Кол-во итераций"); //вывод на экран
fprintf(f,"%s\t","Критерий точности"); //и в файл
fprintf(f,"%s\n","Кол-во итераций");
double krT0=1e-7; //начинается цикл решения
for(int i=0; i<25; i++) //25 точек для установления зависимости вполне должно хватить
{
double itter=0;
int N=1;
do
{
itter++; //текущая иттерация
N=2*N; //кол-во отрезков для интегрирования с каждым разом удваивается
if(selectedMethod==1) //если был выбран метод 1, запускается функция для определения критерия точности, используящая в вычислении метод Трапеций
krT=calcKritCorrectTrapecia(selectedOtnoshenie,selectedFunction,a,b,N,m);
if(selectedMethod==2) //вычисление при помощи метода Симпсона
krT=calcKritCorrectSimpson(selectedOtnoshenie,selectedFunction,a,b,N,m);
}
while(krT>krT0); //выполняется до тех пор пока критерий точности не будет меньше или равным заданомму
cout<<krT0<<"\t\t\t"<<itter<<"\n"; //выводим на экран и в файл
fprintf(f,"%e",krT0);
fprintf(f,"\t%f\n",itter);
krT0=pow(10,0.166666667)*krT0; //увеличиваем критерий точности в 10^(1/24) раз, чтоб получить 25 точку как раз равную 10^-3
} //заканчиваем выполнение цикла на 25 прохождении
cout<<"\nНажмите для возврату к нужному пункту:\n1 - выбор делителя\n2 - выбор метода\n3 - выбор функции\nESC - возврат к самому началу\n";
key=_getch(); //даем шанс вернуться к нужному пункту меню
if(key==27) main(); //если нажмем ESC то вернемся в самое-самое начало
fclose(f); //закрываем файл
Zavisimost1(key,selectedOtnoshenie,selectedMethod,selectedFunction); //и возвращаемся к началу этой функции
}
//ниже функция, вычисляющая значения для зависимости критерия точности от заданного кол-ва итераций
void Zavisimost2(char key,int selectedOtnoshenie,int selectedMethod,int selectedFunction)
{
FILE *f;
f=fopen("D:\\Zavisimost2.txt","at"); //файл для записи
fprintf(f,"%s","Данные для построения зависимости критерий точности от кол-ва итераций\t\n");
double krT; //критерий точности, куда записывается в дальнейшем значение полученное из вне
do //тот же цикл что и в предыдущей функции
{
if (key==49) selectedOtnoshenie=selectedOtnoshenieFunction(f,2);
if (key==49||key==50) selectedMethod=selectedMethodFunction(f,2,selectedOtnoshenie);
if (key==49||key==50||key==51) selectedFunction=selectedFunctionFunction(f,1,selectedOtnoshenie,selectedMethod);
else {cout<<"\nПожалуйста еще разок";key=_getch();}
}
while((key!=49)&&(key!=50)&&(key!=51));
double a = selectedNizhPredel(f,2,selectedOtnoshenie,selectedMethod,selectedFunction); //те же числа
double b = selectedVerhPredel(f);
double m = selectedKoefM(f);
fprintf(f,"%s\t","Кол-во итераций");
fprintf(f,"%s\n","Критерий точности");
char verhPredelIsled = uvelicVerhPredel(); //нужно ли исследование влияние увеличения верхнего предела интегрирования?
int jj;
if (verhPredelIsled=='Y'||'y') jj=10; //если да, то все исследования проводим 10 раз с разными значениями b
else jj=1;
for (int j=0;j<jj;j++)
{
int N=1;
for(int i=1; i<21; i++) //цикл, увеличивающий кол-во итераций с каждым разом на один
{
N=N*2; //а кол-во отрезков для интегрирования в 2 раза
if(selectedMethod==1)
krT=calcKritCorrectTrapecia(selectedOtnoshenie,selectedFunction,a,b,N,m); //те же методы
if(selectedMethod==2)
krT=calcKritCorrectSimpson(selectedOtnoshenie,selectedFunction,a,b,N,m);
cout<<"\nkrT="<<krT<<"\ni="<<i<<"\nN="<<N/2<<"\n";
fprintf(f,"%d\t",i); // выводим все на экран и в файл
fprintf(f,"%e\n",krT);
}
b=b+0.5; //увеличение верхнего предела
}
cout<<"\nНажмите для возврату к нужному пункту:\n1 - выбор делителя\n2 - выбор метода\n3 - выбор функции\nESC - возврат к самому началу\n";
key=_getch(); //опять же свобода выбора, гуляем по просторам нашей программыы))
if(key==27) main();
fclose(f);
Zavisimost2(key,selectedOtnoshenie,selectedMethod,selectedFunction);
}
//файл ReturnKurs.cpp, здесь описанны функции для подсчетов, вычислений, решений и тому подобное...
#include "stdafx.h"
#include "Kursovoy.h"
double calcKritCorrectTrapecia(int selectedOtnoshenie,int selectedFunction,double a,double b,int N,double m) //вычисляет критерий точности с помощью метода трапеций
{
double prevI,I,tempI;
prevI=Trapecia(N/2,a,b,selectedFunction,m);
I=Trapecia(N,a,b,selectedFunction,m);
if(selectedOtnoshenie==2) tempI=analitIntegral(selectedFunction,a,b,m);
if(selectedOtnoshenie==1) tempI=prevI;
return(abs((prevI-I)/tempI));
}
double calcKritCorrectSimpson(int selectedOtnoshenie,int selectedFunction,double a,double b,int N,double m)//с помощью метода Симпсона
{
double prevI,I,tempI;
prevI=Simpson(N/2,a,b,selectedFunction,m);
I=Simpson(N,a,b,selectedFunction,m);
if(selectedOtnoshenie==2) tempI=analitIntegral(selectedFunction,a,b,m);
if(selectedOtnoshenie==1) tempI=prevI;
return(abs((prevI-I)/tempI));
}
double Trapecia(int N,double a,double b,int selectedFunction,double m) //вот ОН - сам метод трапеций
{
double I,h,x; //переменные значение интеграла, шаг по пределу интегрирования, значение аргумента на данном шаге
x=a;
h=(b-a)/N; //так вычислется h
I=h*(selectedFunctionValue(selectedFunction,b,m)+selectedFunctionValue(selectedFunction,a,m))/2;//первое значение интеграла при не разбиении его вообще на отрезки
for(int i=0;i<N;++i) //на каждом шаге
{
x=x+h;
I=I+h*selectedFunctionValue(selectedFunction,x,m);//к значению прибавляется значение функции в данной точке умноженное на значение аргумента
}
return I; //возвращается значение интеграла (конечно же не точное, в ином случае смысла в этой программе не было бы совсем)
}
double Simpson(int N,double a,double b,int selectedFunction,double m) //не менее важный метод Симпсона
{
double I,h,x; //тоже самое
h=(b-a)/N;
I=h*(selectedFunctionValue(selectedFunction,b,m)+selectedFunctionValue(selectedFunction,a,m))/3;//но первое значение чуть по другой формуле
x=a;
for(int i=1;i<N;++i) //два цикла, для четных x и нет, этот для четных
{
x=x+2*h; //т.е от первоначального значения отдаляемся на два шага
I=I+2*h*selectedFunctionValue(selectedFunction,x,m)/3; //и прибавляем
i++;
}
x=a-h; //для нечетных нужно первый раз отдалиться на один h
for(int i=0;i<N;++i)
{
x=x+2*h; //а затем уже делать по два шага
I=I+4*h*selectedFunctionValue(selectedFunction,x,m)/3; //ну и формула, и всё всё складываем
i++;
}
return I; //возвращаем полученное значение
}
double selectedFunctionValue(int selectedFunction,double argumentValue,double m) //вычислет значения заддоной функции при заданных параметрах
{
switch(selectedFunction)
{
case 1:return (m/(argumentValue*argumentValue));break;
case 2:return (m/(argumentValue));break;
case 3:return (sin(m*argumentValue));break;
default:return 0;break;
}
}
double analitIntegral(int selectedFunction,double a,double b, double m) //аналитическое значение интеграла, ну тут все понятно
{
switch(selectedFunction)
{
case 1:return m*((1/a)-(1/b));break;
case 2:return m*((log(b))-(log(a)));break;
case 3:return 1/m*((cos(m*a))-(cos(m*b)));break;
default:return 0;break;
}
}
//файл Select.cpp, самое сложное))) функции выбора, ввода параметров, интерфейс, не побоюсь этого слова))
#include "stdafx.h"
#include "Kursovoy.h"
int selectZavisimost() //вывод на экран меню выбора требуемой зависимости (вызывается в самом начале)
{ int numberZavisimost;
Zagolovok();
cout<<"Выберите зависимость:\n"
<<"1. кол-во итераций от критерия точности\n"
<<"2. точность от кол-ва итераций\n"
<<"Выбранная зависимость - ";
cin>>numberZavisimost;
return numberZavisimost;
}
int selectedZavisimostFunction() //если же таких зависимостей не обнаруживается (их всего две)
{
int selectedZavisimost=selectZavisimost();
while (selectedZavisimost!=1&&selectedZavisimost!=2)
{
cout<<"Данная зависимость не обнаружена, выберите заново..."; //то выводим на экран такое сообщение,
selectedZavisimost=selectZavisimost(); //и даем возможность, т.е заставляем, выбрать снова
}
if(selectedZavisimost==1) Zavisimost1(49,1,0,0); //вызывается требуемая функция (с параметрами 49, т.е дальнейший выбор данных будет полным)
if(selectedZavisimost==2) Zavisimost2(49,1,0,0);
return selectedZavisimost; //а ничкому не возвращает ничего, ну и пусть
}
int selectOtnoshenie() //меню выбора делителя для критерия точности
{ int numberOtnoshenie;
cout<<"\nВыберите делитель при вычислении критерия точности:\n"
<<"1. значение интеграла на предыдущем прохождении\n"
<<"2. аналитическое значение интеграла\n"
<<"Выбранный делитель - ";
cin>>numberOtnoshenie;
return numberOtnoshenie;
}
int selectedOtnoshenieFunction(FILE*f,int selectedZavisimost)
{
system("cls");
Zagolovok();
cout<<"Выбранная зависимость - " //выводит номер уже выбранной ранее зависимости
<<selectedZavisimost;
int selectedOtnoshenie=selectOtnoshenie();
while (selectedOtnoshenie!=1&&selectedOtnoshenie!=2) //и пока нужный делитель для вычисления критерия не будет выбран
{
cout<<"Данный пункт не найден..."; //выводится данное сообщение
selectedOtnoshenie=selectOtnoshenie(); //и снова выбираем
}
fprintf(f,"%s%d%s","Выбранное отношение для критерия точности -",selectedOtnoshenie,"\t\n");
return selectedOtnoshenie;
}
int selectMethod() //далее всё так же как и в предыдущих пунктах выбора
{ int numberMethod;
cout<<"\nВыберите метод:\n"
<<"1. Метод трапеций\n"
<<"2. Метод Симпсона\n"
<<"Выбранный метод - ";
cin>>numberMethod;
return numberMethod;
}
int selectedMethodFunction(FILE*f,int selectedZavisimost,int selectedOtnoshenie)
{
system("cls");
Zagolovok();
cout<<"Выбранная зависимость - "
<<selectedZavisimost
<<"\nВыбранный делитель - "
<<selectedOtnoshenie;
int selectedMethod=selectMethod();
while (selectedMethod!=1&&selectedMethod!=2)
{
cout<<"метод не найден, выберите снова...";
selectedMethod=selectMethod();
}
fprintf(f,"%s%d%s","Выбранный метод -",selectedMethod,"\t\n");
return selectedMethod;
}
int selectFunction()
{
int numberFunction;
cout<<"\nВыберите функцию:\n"
<<"1. f(x) = m/x^2\n"
<<"2. f(x) = m/x\n"
<<"3. f(x) = sin(mx)\n"
<<"Выбранная функция - ";
cin>>numberFunction;
return numberFunction;
}
int selectedFunctionFunction(FILE*f,int selectedZavisimost,int selectedOtnoshenie, int selectedMethod)
{
system("cls");
Zagolovok();
cout<<"Выбранная зависимость - "
<<selectedZavisimost
<<"\nВыбранный делитель - "
<<selectedOtnoshenie
<<"\nВыбранный метод -"
<<selectedMethod;
int selectedFunction=selectFunction();
while (selectedFunction!=1&&selectedFunction!=2&&selectedFunction!=3)
{
cout<<"Функция не найдена, выберите снова...";
selectedFunction=selectFunction();
}
fprintf(f,"%s%d%s","Выбранная функция -",selectedFunction,"\t\n");
return selectedFunction;
}
double selectedNizhPredel(FILE*f,int selectedZavisimost,int selectedOtnoshenie, int selectedMethod, int selectedFunction) //вводим нижний предел
{
system("cls");
Zagolovok();
cout<<"Выбранная зависимость - "
<<selectedZavisimost
<<"\nВыбранный делитель - "
<<selectedOtnoshenie
<<"\nВыбранный метод -"
<<selectedMethod
<<"\nВыбранная функция - "
<<selectedFunction;
double a;
cout<<"\nНижний предел интегрирования a=";
cin>>a;
fprintf(f,"%s%f%s","Нижний предел интегрирования a=",a,"\t\n");
return a;
}
double selectedVerhPredel(FILE*f) //и верхний
{
double b;
cout<<"Верхний предел интегрирования b=";
cin>>b;
fprintf(f,"%s%f%s","Верхний предел интегрирования b=",b,"\t\n");
return b;
}
double selectedKoefM(FILE*f)
{
double m; //ну и почти не нужный коэффициент (используем в нашей задаче только для синуса)
cout<<"Коэффициент m=";
cin>>m;
cout<<"\n\nИдет вычисление...\n в зависимости от параметров процесс может занять некоторое время\n";
fprintf(f,"%s%f%s","Коэффициент m=",m,"\t\n");
return m;
}
char uvelicVerhPredel()
{
char a;
cout<<"провести исследование при увелении верхнего предела?? Y???";
cin>>a;
return a;
}
void Zagolovok() //а это самая главная часть программы, без которой ничего работь не будет
{ //выводит на экран КУРСОВАЯ, для красоты, ну или для подобия красоты
cout<<"* * * * ** * * * * * * * * * * \n"
<<"* * * * * * * * * * * * * * * \n"
<<"** * ** * * * * * * * * * * \n"
<<"* * * * * * * * * * * * * * \n"
<<"* * * * * * * * * * * * * * \n"
<<"___________________________________________________ \n\n";
}
Похожие работы
... . Также мы получим графическое отображение процесса интегрирования на участках возрастания и убывания функции. 2. Выбор математической модели задачи Кратко рассмотрим основные методы численного интегрирования и выясним почему метод Гаусса наиболее подходит для решения нашей задачи. 2.1 Метод прямоугольников Метод прямоугольников получается при замене подынтегральной функции на ...
... - 0.588. 2. Математические и алгоритмические основы решения задачи Кратко рассмотрим основные методы численного интегрирования и выясним, почему самый лучший и быстрый метод интегрирования - десятиточечный метод Гаусса. 2.1 Метод прямоугольников Метод прямоугольников получается при замене подынтегральной функции на константу. В качестве константы можно взять значение функции в любой ...
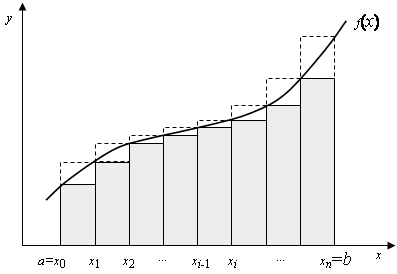
... – остаточный член, характеризующий погрешность формулы. Заметим, что формулы вида (2) называют квадратурными формулами. Геометрический смысл численного интегрирования состоит в вычислении площади криволинейной трапеции, ограниченной графиком функции f(х), осью абсцисс и двумя прямыми х = а и х = b. Приближенное вычисление площади приводит к отбрасыванию в квадратурных формулах остаточного члена ...
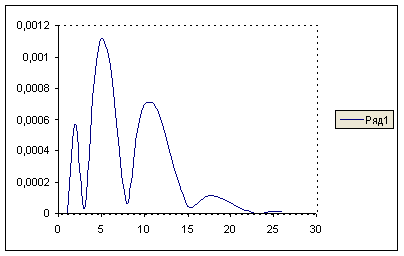
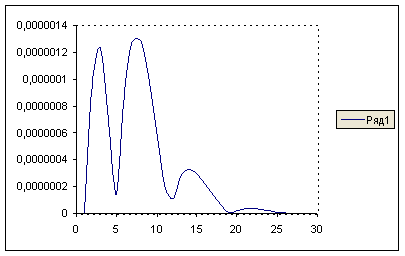
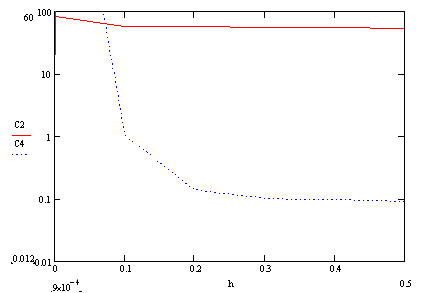
... для курсовой работы, заключающегося в интегрирования ОДУ, была составлена и отлажена программа, приведенная в приложении А. С помощью данной программы проведена серия опытных исследований свойств методов Рунге-Кутты второго и четвёртого порядков. При задании определенного интервала значений шага интегрирования ошибка интегрирования уменьшается с уменьшением шага. Подтверждение сего факта можно ...



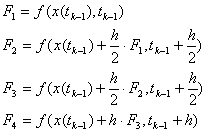
0 комментариев