Координаты центра тяжести определяем по формулам

1. Координаты центра тяжести определяем по формулам

;

Площади фигур определяются по формулам:

Прямоугольник: A = bh

A₁ = 26*32 = 832 см²;

Окружность: A = pr²

A₂ = 3,14*3² = 28,26 см²;

Проведем вспомогательные оси координат через левый и нижний габариты фигуры и определим для этого положения координаты центра тяжести. Координаты центра тяжести прямоугольника лежат на пересечении диагоналей и легко определяются графически. Координата центра тяжести окружности находится в ее центре и также может быть определена простым замером. Очевидно, что координата X_C cоставной фигуры, показанной на рис. 1, лежит на оси симметрии, что должно подтвердиться расчетом

X_C = (832*13 – 28,26*13)/(832-28,26) = 13 см

Y_C = (832*16 – 28,26*29)/(832-28,26) = 15,5429 см

Через центр тяжести проводим центральные оси.

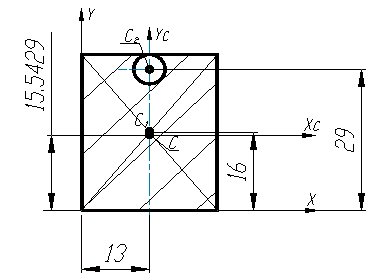
Рис. 2. Определение координат центра тяжести составной фигуры

2. Осевые моменты инерции сечения определяем по формулам

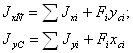
Моменты инерции для элементарных фигур равны:

Прямоугольник: J_x = bh³/12; J_y=hb³/12

Окружность: J_x = J_y= pd⁴/64

Определяем численные значения:

Прямоугольник:

эпюра напряжение энергия деформация

J_x1 = (26*32³)/12 = 70997,33 см⁴;

J_y1 = (32*26³)/12 = 46869,33 см⁴;

Окружность:

J_x = J_y= 3,14 * 6⁴/64 = 63,59 см⁴;

J_xС = 70997,33+ 832*0,4571 - (63,59 + 28,26*13,4571) = 70933,7496 см⁴

J_y = 46869,33 + 832*0 - (63,59 + 28,26*0) = 46805,74см⁴

3. Две взаимно перпендикулярные оси, из которых хотя бы одна является осью симметрии фигуры будут ее главными осями, а главные оси, проходящие через центр тяжести сечения называются главными центральными осями. Таким образом , оси Хс и Yc совпадают с осями U и V, так как ось Yc проходит через ось симметрии фигуры, а обе оси вместе проходят через центр тяжести.

Задача 6

Для балки, показанной на рис. 1, требуется:

1. Построить эпюры изгибающих моментов и поперечных сил

2. Подобрать для балки размеры прямоугольного сечения bxh при расчетном сопротивлении R=10 МПа;

3. Для сечения с наибольшей поперечной силой построить эпюру касательных напряжений

Рис. 1. Расчетная схема

а = 3,6 м, h = 2b

q = 4 кН/м

F = 10 кН;

M = 150 кН м.

Решение:

Предварительно примем, что реакции опор направлены: вверх и составим уравнения моментов относительно точек А и В.

Рис.2

SM(_A) = 0

R_B*4a + F*3а - M - q*2a² = 0;

R_B = (M + q*2a² – 3Fa) /4a ;

R_B = (150 +4*2*3,6² -3*10*3,6) / (4*3,6) = 10,117 кН ;

SM(_B) = 0

q*2a*3a - Fa - R_А*4a – M = 0;

R_А = (q*6a² - Fa - M)/ 4a ;

R_А = (4*6*3,6² - 10*3,6 - 150) /(4*3,6) = 8,683 кН ;

Для проверки составим систему уравнений проекций сил на ось Y

SP(Y) = 0

R_A + R_B – q2a + F = 0;

8,683 + 10,117 - 4*2*3,6 + 10 = 0,0

Расчет верен.

Из суммы проекций сил на ось Х очевидно, что реакция Rx в точке В равна 0.

Для построения эпюр следует рассмотреть балку в характерных сечениях. При построении эпюры Q сосредоточенные силы вызывают скачок эпюры, а моменты не оказывают на нее влияния.

При построении эпюры М рассматривается влияние сил, оставшихся на рассматриваемой части балки на точку сечения. При этом учитывается только влияние моментов. Изгибаюший момент вызывает скачок на величину момента,

Для построения эпюры М требуется найти координату экстремального значения изгибающего момента в опасном сечении, определяемом положением точки на эпюре поперечных сил, где Q = 0. Из эпюры видно, что это координата z. Так как треугольники, образованные наклонной линией от распределенной нагрузки подобны, то соотношения их соответствующих сторон одинаковы, тогда

z = 3,6 / (1+ 1/(8,683/20,117)) = 1,085 м

Величину экстремального момента удобнее определить из рассмотрения левой части балки при сечении возле координаты z.

Мz + qz²/2 – R_Аz = 0

Мz = R_Аz - qz²/2 = 8,683*1,085 - 4*1,085²/2 = 7,067 кН м

В сечении по точке приложения силы F удобнее рассматривать левую часть балки, заменяя отсеченную часть внутренним моментом, который равен

М_F = R_Ba = 10,117*3,6 = 36,421 кН м

В сечении по точке приложения сосредоточенного момента М удобнее рассматривать левую часть балки, заменяя отсеченную часть внутренним моментом, который равен

М_М2 = R_B*2a + F * a = 10,117*2*3,6 + 10*3,6 = 108,842 кН м

Величина момента слева от точки приложения сосредоточенного момента М определяется скачком на величину момента

М_М1 = М_М2 – М = 108,842-150 = -41,158 кН м

Расчеты показывают, что сечение в точке приложения сосредоточенного момента М является самым нагруженным и, следовательно, наиболее опасным

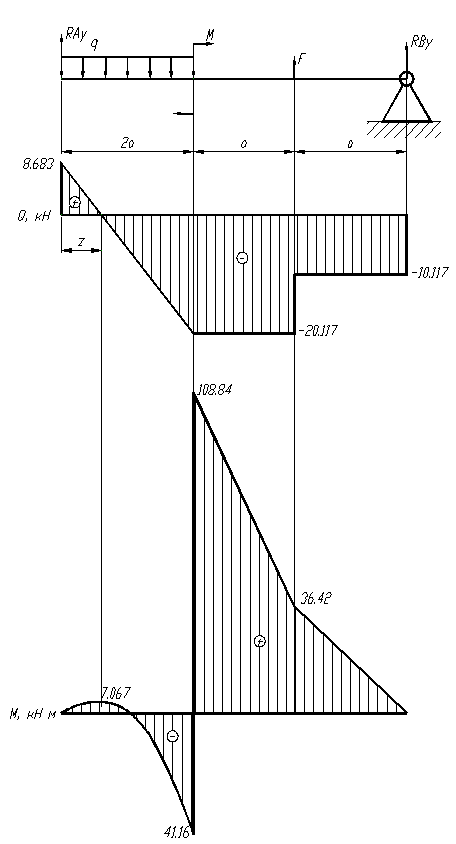
Рис. 3. Эпюры поперечных сил Q и изгибающих моментов M.

Условие прочности для балки выглядит следующим образом

По условию задачи дано:

[s] = R = 10 МПа = 1 кН/см²,

Подставляя эти значения,

M_max = 108,842 кН м = 10884,2 кН см

W_x = 10884,2 / 1 = 10884,2 см³

Для прямоугольника W_x = bh²/6 , тогда при условии h = 2b

W_x = b(2b)²/6 = 4b³/6

b =  = 25,368 см

h = 2b = 2*25,368 = 50,736 см

Принимаем сечение 26х52 см с площадью A = 26*52 = 1352 cм²

Определяем касательные напряжения в точке с наибольшей поперечной силой. Это также точка приложения сосредоточенного момента М

,

где k – коэффициент, зависящий от формы сечения. Для прямоугольного сечения k = 1,5.

t_max = 1,5 * 20,117 / 1352 = 0,022 кН/см² = 0,22 МПа

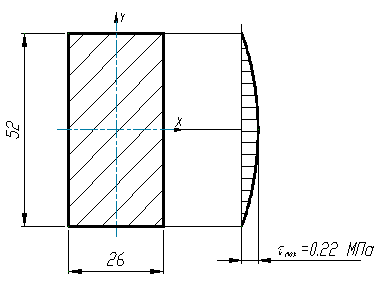
Рис. 4. Эпюра касательных напряжений

Задача 7

Для заданной схемы требуется:

1. Построить эпюры изгибающих моментов и поперечных сил;

2. Подобрать по ГОСТ двутавровое сечение балки, принимая расчетное сопротивление изгибу R_и = 160 МПа

3. Построить в опасном сечении эпюру нормальных напряжений

4. В сечении с наибольшей поперечной силой построить эпюру касательных напряжений.

Рис. 1. Расчетная схема .

Исходные данные:

а = 3,6 м,

q = 4 кН/м

F = 10 кН;

M = 150 кН м.

2. Отбросим заделку, заменив ее действие действием сил реакции. В сплошной заделке возникает три реакции: Момент M_Rи две реакции Rx и Ry.

Рис. 2. Расчетная схема

Составим уравнения равновесия, приняв направление по часовой стрелке за отрицательное, а против часовой стрелки – за положительное.

SM(_A) = 0

M_R – М - qa*1,5а + F*2a = 0;

M_R = M + 1,5qa² - 2Fa;

M_R =150 + 1,5*4*3,6² – 2*10*3,6 =155,76 кН м;

Составим систему уравнений проекций сил на ось Y

SP(Y) = 0

Ry + F – qa = 0;

Ry = qa-F = 4*3,6-10 =4,4 кН;

Из построения проекций сил на ось Х видно, что реакция R_X = 0.

Для построения эпюр следует рассмотреть балку в характерных сечениях. При построении эпюры Q сосредоточенные силы вызывают скачок эпюры, а моменты не оказывают на нее влияния. На участке действия распределенной нагрузки эпюра выражается наклонной линией. При построении эпюры М рассматривается влияние сил, оставшихся на рассматриваемой части балки на точку сечения. При этом учитывается только влияние моментов. Изгибаюший момент вызывает скачок на величину момента. Рассмотрим более подробно сечения в характерных точках балки. На первом участке отбрасываем правую часть балки, заменяя ее действием внутреннего момента М₁, тогда

-М₁ + M_R – Ryа =0

М₁ = M_R – Ryа =155,76-4,4*3,6 = 139,92 кН м

На третьем участке отсечем левую часть балки. Для оставшейся части уравнение равновесия будет равно

М₃ - M= 0

М₃ = M= 150 кН м

На втором участке эпюра выражается параболической кривой с перегибом в точке, соответствующей координате z.

z = 3,6 / (1+ 1/(4,4/10)) = 1,100 м

Уравнение равновесия для координаты Z рассматриваем, отбросив правую часть балки.

-М₂ + M_R – Ry(а+z)+q*z²/2 = 0

М₂ = M_R – Ry(а+z)+q*0,125a² = 155,76-4,4*4,7+2*1,1² = 137,500 кН м

Рис. 3. Эпюры N и М.

Условие прочности для балки выглядит следующим образом

По условию задачи [s] = R_и = 160 МПа = 16 кН/см²,

Подставляя эти значения,

M_max = 155,76 кН м = 15576 кН см

W_x = 15576 / 16 = 973,5 см³

Параметры двутавра подбираем по справочнику. Ближайшая подходящая балка - №45, имеющая W_x = 1231 см³, при площади сечения А = 84,7 см².

Максимальное значение напряжения составит

 = 15576 / 1231 = 12,65 кН/см² = 126,5 МПа

Согласно закону распределения нормальных напряжений имеем

= 15576 / 27696 * 45/2 = 12,65 МПа

Рис. 4. Эпюра нормальных напряжений для опасного сечения

Наибольшая поперечная сила наблюдается в сечении, где приложена сила F. Для этой точки касательное напряжение равно в соответствии с формулой Журавского

,

где d – толщина стенки двутавра

t_max = 10*708 / (27696*0,9) = 0,28 кН/см² = 2,8 МПа

В месте соприкосновения полок со стенкой касательные напряжения определяются как

,

где — статический момент полки двутавра относительно оси Х, равный

=16*1,42(45/2-1,42/2) = 495,07 см³

t_А = 10*495,07 / (27696*0,9) = 0,171 кН/см² = 1,71 МПа

Касательными напряжениями на полках двутавровой балки можно пренебречь ввиду их незначительности

Рис. 5. Касательные напряжение в двутавровой балке в точке действия наибольших перерезывающих сил.