Место занимает прирост финансовых активов. Наибольшее значение в 1 кластере

2 место занимает прирост финансовых активов. Наибольшее значение в 1 кластере.

Наименьший коэффициент в 1 и 2 кластерах у «приобретение недвижимости», а в 3 кластере выявлено заметное уменьшение денег на руках у населения.

В целом особое значение для населения имеет покупка товаров и оплата услуг и незначительное покупка недвижимости.

4)  сравнить полученную классификацию с результатами применения алгоритма внутригрупповых связей.

В анализе межгрупповых связей ситуация практически не изменилась, за исключением Тамбовской области, которая из 2 кластера попала в 1.(Рис.13)

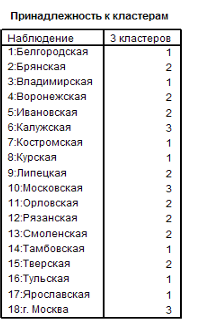
Рис. 13 Анализ внутригрупповых связей

В таблице «Средних значений» никаких изменений не произошло.

Глава 3. Факторный анализ

Задание: Анализ деятельности предприятий легкой промышленности.

Имеются данные обследований 20 предприятий легкой промышленности (Рис. 14) по следующим характерным признакам:

·  Х1 – уровень фондоотдачи;

·  Х2 – трудоемкость единицы продукции;

·  Х3 – удельный вес закупочных материалов в общих расходах;

·  Х4 – коэффициент сменности оборудования;

·  Х5 – премии и вознаграждения на одного работника;

·  Х6 – удельный вес потерь от брака;

·  Х7 – среднегодовая стоимость основных производственных фондов;

·  Х8 – среднегодовой фонд заработной платы;

·  Х9 – уровень реализуемости продукции;

·  Х10 – индекс постоянного актива (отношение основных средств и прочих внеоборотных активов к собственным средствам);

·  Х11 – оборачиваемость оборотных средств;

·  Х12 – непроизводственные расходы.

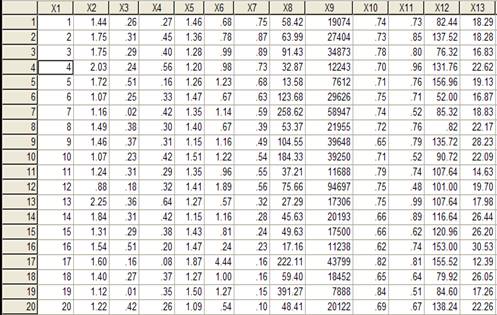
Рис.14 Исходные данные

Требуется:

1.  провести факторный анализ следующих переменных: 1,3,5-7, 9, 11,12, выявить и интерпретировать факторные признаки;

2.  указать наиболее благополучные и перспективные предприятия.

Выполнение:

1.  Провести факторный анализ следующих переменных: 1,3,5-7, 9, 11,12, выявить и интерпретировать факторные признаки.

Факторный анализ – это совокупность методов, которые на основе реально существующих связей объектов (признаков) позволяют выявить латентные (неявные) обобщающие характеристики организационной структуры.

В диалоговом окне факторного анализа выбираем наши переменные, указываем необходимые параметры.

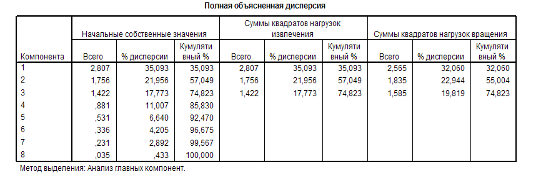
Рис. 15 Полная объясненная дисперсия

По таблице «Полной объясненной дисперсии» видно, что выделены 3 фактора, объясняющие 74,8 % вариаций переменных – построенная модель достаточно хорошая.

Теперь интерпретируем факторные признаки по «Матрице повернутых компонент»: (Рис.16).

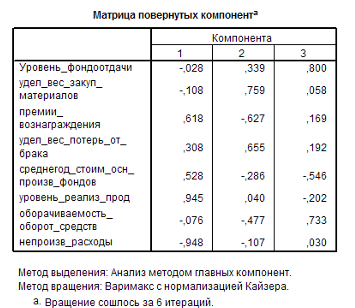
Рис. 16 Матрица повернутых компонент

Фактор 1 наиболее тесно связан с уровнем реализации продуктов и имеет обратную зависимость от непроизводственных расходов.

Фактор 2 наиболее тесно связан с удельным весом закупочных материалов в общих расходах и удельным весом потерь от брака и имеет обратную зависимость от премий и вознаграждений на одного работника.

Фактор 3 наиболее тесно связан с уровнем фондоотдачи и оборачиваемость оборотных средств и имеет обратную зависимость от среднегодовой стоимости основных производственных фондов.

2.  Указать наиболее благополучные и перспективные предприятия.

Для того, чтобы выявить наиболее благополучные предприятия проведем сортировку данных по 3 факторным признакам по убыванию. (Рис.17)

  

Рис. 17

Наиболее благополучными предприятиями следует считать: 13,4,5, так как в целом по 3 факторам их показатели занимают наиболее высокие и стабильные позиции.

Глава 4. Дискриминантный анализ

Оценка кредитоспособности юридических лиц в коммерческом банке

В качестве значимых показателей, характеризующих финансовое состояние организаций-заемщиков, банком выбраны шесть показателей (табл. 4.1.1):

QR (Х1) — коэффициент срочной ликвидности;

CR (Х2) — коэффициент текущей ликвидности;

EQ/TA (Х3) — коэффициент финансовой независимости;

TD/EQ (Х4) — суммарные обязательства к собственному капиталу;

ROS (Х5) — рентабельность продаж;

FAT (Х6) — оборачиваемость основных средств.

Таблица 4.1.1. Исходные данные

Заемщик	QR	CR	EQ/TA	TD/EQ	ROS, %	FAT, раз
1	0,614	2,982	0,592	0,303	13,179	2,712
2	8,604	4,496	0,284	0,109	17,181	10,115
3	6,207	4,423	0,366	0,228	15,385	2,151

Требуется:

На основе дискриминантного анализа с использованием пакета SPSS определить, к какой из четырех категорий относятся три заемщика (юридических лица), желающие получить кредит в коммерческом банке:

-   Группа 1 — с отличными финансовыми показателями;

-   Группа 2 — с хорошими финансовыми показателями;

-   Группа 3 — с плохими финансовыми показателями;

-   Группа 4 — с очень плохими финансовыми показателями.

По результатам расчета построить дискриминантные функции; оценить их значимость по коэффициенту Уилкса (λ). Построить карту восприятия и диаграммы взаимного расположения наблюдений в пространстве трех функций. Выполнить интерпретацию результатов проведенного анализа.

Ход выполнения:

Для того чтобы определить, к какой из четырех категорий относятся три заемщика, желающие получить кредит в коммерческом банке, строим дискриминантный анализ, который позволяет определить, к какой из ранее выявленных совокупностей (обучающих выборок) следует отнести новых клиентов.

В качестве зависимой переменной выберем группу, к которой может относиться заемщик в зависимости от его финансовых показателей. Из данных задачи, каждой группе присваивается соответствующая оценка 1, 2, 3 и 4.

Ненормированные канонические коэффициенты дискриминантных функций, приведенные на рис. 4.1.1, используются для построения уравнения дискриминантных функций D1(X), D2(X) и D3(X):

1.) D1(X) =

2.) D2(X) =

3.) D3(X) =

Функция

1 2 3 Х1 ,064 ,363 -,021 Х2 1,818 2,073 -,573 Х3 9,328 -10,089 4,726 Х4 ,002 ,003 ,002 Х5 ,129 ,048 -,097 Х6 ,147 ,092 ,026 (Константа) -6,112 1,170 -1,183

Рис. 4.1.1. Коэффициенты канонической дискриминантной функции

Проверка функции(й)	Лямбда Уилкса	Хи-квадрат	ст.св.	Знч.
от 1 до 3	,017	139,005	18	,000
от 2 до 3	,472	25,502	10	,004
3	,878	4,436	4	,350

Рис. 4.1.2. Лямбда Уилкса

Однако, поскольку значимость по коэффициенту Уилкса (рис. 4.1.2) второй и третей функции более 0.001, их для дискриминации использовать нецелесообразно.

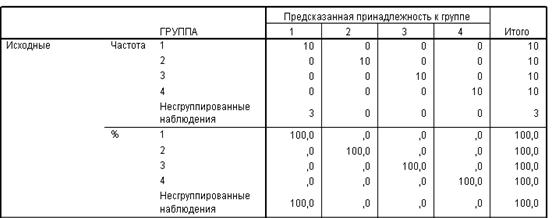
Данные таблицы «Результаты классификации» (рис. 4.1.3) свидетельствуют о том, что для 100 % наблюдений классификация проведена корректно, высокая точность достигнута во всех четырех группах (100 %).

Рис. 4.1.3. Результаты классификации

Информация о фактических и предсказанных группах для каждого заемщика приведены в таблице «Поточечные статистики» (рис. 4.1.4).

В результате дискриминантного анализе высокой вероятностью определена принадлежность новых заемщиков банка к обучающему подмножеству М1 – первый, второй и третий заемщик (порядковый номера 41, 42, 43) отнесены к подмножеству М1 с соответствующими вероятностями 100 %.

Номер наблюдения	Фактическая группа	Наивероятнейшая группа
		Предсказанная группа	P(D>d | G=g)		P(G=g | D=d)
			p	ст.св.
1	1	1	0,317601242	3	0,99
...	...	...	...	...	...
41	несгруппированные	1	0,107179896	3	1
42	несгруппированные	1	3,07013E-34	3	1
43	несгруппированные	1	4,13563E-21	3	1

Рис. 4.1.4. Поточечная статистика

Координаты центроидов по группам приведены в таблице «Функции в центроидах групп» (рис. 4.1.5). Они используются для нанесения центроидов на карту восприятия (рис. 4.1.6).

ГРУППА

Функция

1 2 3 1 7,831 ,610 ,036 2 ,309 -1,455 ,179 3 -2,792 ,074 -,579 4 -5,348 ,771 ,365

Рис. 4.1.5. Функции в центроидах групп

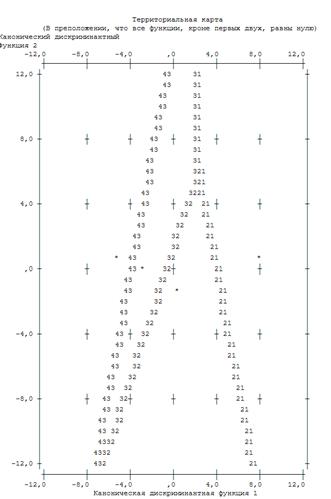
Рис. 4.1.6. Карта восприятия для двух дискриминантных функций D1(X) и D2(X) (* — центроид группы)

Поле «Территориальной карты» разделено дискриминантными функциями на четыре области: в левой части находятся преимущественно наблюдения четвертой группы заемщиков с очень плохими финансовыми показателями, в правой части — первой группы с отличными финансовыми показателями, в средней и нижней части — третьей и второй группы заемщиков с плохими и хорошими финансовыми показателями соответственно.

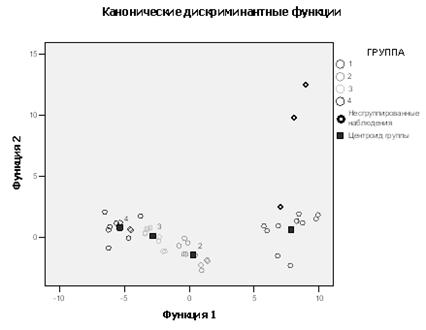
Рис. 4.1.7. Диаграмма рассеяния для всех групп

На рис. 4.1.7 приведен объединенный график распределения всех групп заемщиков вместе со своими центроидами; его можно использовать для проведения сравнительного визуального анализа характера взаимного расположения групп заемщиков банка по финансовыми показателями. В правой части графика расположены заемщики с высокими показателями, в левой — с низкой, а в средней части — со средними финансовыми показателями. Поскольку по результатам расчета вторая дискриминантная функция D2(X) оказалась незначима, то различия координат центроидов по этой оси незначительны.

Оценка кредитоспособности физических лиц в коммерческом банке

Кредитный отдел коммерческого банка провел выборочное обследование 30 своих клиентов (физических лиц). На основе предварительного анализа данных, заемщики оценивались по шести показателям (табл. 4.2.1):

Х1 — заемщик брал кредит в коммерческих банках ранее;

Х2 — среднемесячный доход семьи заемщика, тыс. руб.;

Х3 — срок (период) погашения кредита, лет;

Х4 — размер выданного кредита, тыс. руб.;

Х5 — состав семьи заемщика, чел.;

Х6 — возраст заемщика, лет.

При этом по вероятности возврата кредита выявлены три группы заемщиков:

-   Группа 1 — с низкой вероятностью погашения кредита;

-   Группа 2 — со средней вероятностью погашения кредита;

-   Группа 3 — с высокой вероятностью погашения кредита.

Требуется:

На основе дискриминантного анализа с использованием пакета SPSS необходимо классифицировать трех клиентов банка (по вероятности погашения кредита), т.е. оценить принадлежность каждого из них к одной из трех групп. По результатам расчета построить значимые дискриминантных функции, их значимость оценить по коэффициенту Уилкса (λ). В пространстве двух дискриминантных функций для каждой группы построить диаграммы взаимного расположения наблюдений и объединенную диаграмму. Оценить место расположения каждого заемщика на этих диаграммах. Выполнить интерпретацию результатов проведенного анализа.

Таблица 4.2.1. Исходные данные

Заемщик	Брался ли кредит ранее (1 - да, 2 - нет)	Среднемесячный доход семьи заемщика, тыс. руб.	Период погашения кредита, лет	Размер кредита, тыс. руб.	Состав семьи заемщика, чел.	Возраст заемщика, лет
1	1	36,47	10	450	6	43
2	1	47,37	3	260	4	52
3	1	46,85	9	470	3	44

Ход выполнения:

Для построения дискриминантного анализа в качестве зависимой переменной выберем вероятность своевременного погашения кредита клиентом. Учитывая, что она может быть низкой, средней и высокой, каждой категории присвоим соответствующую оценку 1,2 и 3.

Ненормированные канонические коэффициенты дискриминантных функций, приведенные на рис. 4.2.1, используются для построения уравнения дискриминантных функций D1(X), D2(X):

1.) D1(X) =

2.) D2(X) =

	Функция
	1	2
Брался ли кредит ранее	-2,566	3,291
Среднемесячный доход семьи	,290	,151
Период погашения кредита	,009	,631
Размер кредита	,008	-,009
Состав семьи заемщика, чел	-,876	-,231
Возраст заемщика, лет	,032	,044
(Константа)	-4,286	-11,943

Рис. 4.2.1. Коэффициенты канонической дискриминантной функции

Проверка функции(й)	Лямбда Уилкса	Хи-квадрат	ст.св.	Знч.
от 1 до 2	,104	55,549	12	,000
2	,759	6,757	5	,239

Рис. 4.2.2. Лямбда Уилкса

По коэффициенту Уилкса (рис. 4.2.2) для второй функции значимость более 0.001, следовательно, ее для дискриминации использовать нецелесообразно.

Данные таблицы «Результаты классификации» (рис. 4.2.3) свидетельствуют о том, что для 93,3 % наблюдений классификация проведена корректно, высокая точность достигнута в первой и второй группах (100% и 91,7%), менее точные результаты получены в третьей группе (88, 9%).

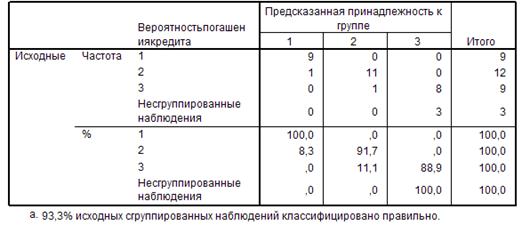
Рис. 4.2.3. Результаты классификации

Информация о фактических и предсказанных группах для каждого клиента приведены в таблице «Поточечные статистики» (рис. 4.2.4).

В результате дискриминантного анализе высокой вероятностью определена принадлежность новых клиентов банка к обучающему подмножеству М3 – первый, второй и третий клиент (порядковый номера 31, 32, 33) отнесены к подмножеству М3 с соответствующими вероятностями 99%, 99% и 100%.

Номер наблюдения	Фактическая группа	Наивероятнейшая группа
		Предсказанная группа	P(D>d | G=g)		P(G=g | D=d)
			p	ст.св.
1	2	2	0,720783301	2	0,97638652
...	...	...	...	...	...
31	несгруппированные	3	0,728612614	2	0,999624597
32	несгруппированные	3	0,000220059	2	0,999999998
33	несгруппированные	3	1,52747E-09	2	1

Рис. 4.2.4. Поточечная статистика

Вероятность погашения кредита	Функция
	1	2
1	-2,873	,503
2	-,289	-,652
3	3,258	,366

Рис. 4.2.5. Функции в центроидах групп

Координаты центроидов по группам приведены в таблице «Функции в центроидах групп» (рис. 4.2.5). Они используются для нанесения центроидов на карту восприятия (рис. 4.2.6).

Поле «Территориальной карты» разделено дискриминантными функциями на три области: в левой части находятся преимущественно наблюдения первой группы клиентов с очень низкой вероятностью погашения кредита, в правой части — третьей группы с высокой вероятностью, в средней — второй группы клиентов со средней вероятностью возврата кредита соответственно.

На рис. 4.2.7 (а – в) отражено расположение клиентов каждой из трех групп на плоскости двух дискриминантных функций D1(X) и D2(X). По этим графикам можно проводить детальный анализ вероятности погашения кредита внутри каждой группы, судить о характере распределения клиентов и оценивать степень их удаленности от соответствующего центроида.

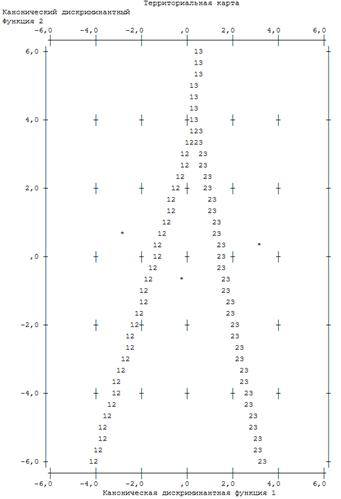
Рис. 4.2.6. Карта восприятия для трех дискриминантных функций D1(X) и D2(X) (* — центроид группы)

Так же на рис. 4.2.7 (г) в той же системе координат приведен объединенный график распределения всех групп клиентов вместе со своими центроидами; его можно использовать для проведения сравнительного визуального анализа характера взаимного расположения групп клиентов банка с разными вероятностями погашения кредита. В левой части графика расположены заемщики с высокой вероятностью погашения кредита, в правой — с низкой, а в средней части — со средней вероятностью. Поскольку по результатам расчета вторая дискриминантная функция D2(X) оказалась незначима, то различия координат центроидов по этой оси незначительны.

б)

г)

а)

в)

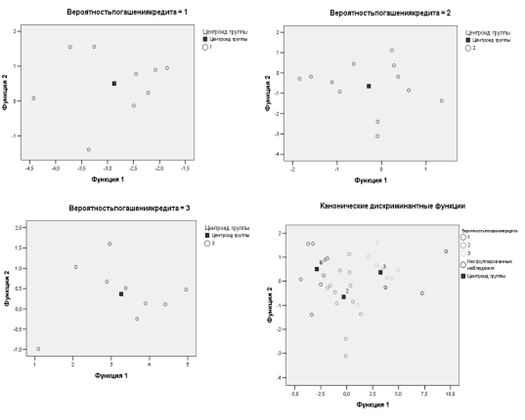
Рис. 4.2.7. Расположение наблюдений на плоскости двух дискриминантных функций для групп с низкой (а), средней (б), высокой (с) вероятностью погашения кредита и для всех групп (г)

Список литературы

1.  «Многомерный статистический анализ в экономических задачах. Компьютерное моделирование в SPSS», Вузовский учебник, 2009 г.

2.  Орлов А.И. «Прикладная статистика» М.: Издательство «Экзамен», 2004

3.  Фишер Р.А. «Статистические методы для исследователей», 1954 г.

4.  Калинина В.Н., Соловьев В.И. «Введение в многомерный статистический анализ» Учебное пособие ГУУ,2003;

5.  Ахим Бююль, Петер Цёфель, «SPSS: искусство обработки информации» Изд-во DiaSoft, 2005г.;

6.  http://ru.wikipedia.org/wiki