Навигация
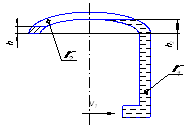
Строим эпюру избыточного давления на поверхность ABMN. Для этого строим эпюры на каждом отдельном участке поверхности
2. Строим эпюру избыточного давления на поверхность ABMN. Для этого строим эпюры на каждом отдельном участке поверхности.
Поскольку резервуар открыт, то эпюра избыточного давления на прямоугольную стенку AB будет представлять собой прямоугольный треугольник с высотой ![]() м и основанием
м и основанием ![]() Па. Строим данный треугольник, используя масштаб (рис.1).
Па. Строим данный треугольник, используя масштаб (рис.1).
Эпюра избыточного давления на наклонную прямоугольную стенку BM будет представлять собой трапецию с основаниями ![]() Па и
Па и ![]() Па и высотой, равной
Па и высотой, равной 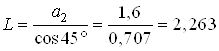 м. Строим эпюру избыточного давления на участке BM.
м. Строим эпюру избыточного давления на участке BM.
Эпюра избыточного давления на вертикальную прямоугольную стенку MN будет представлять собой также трапецию с основаниями ![]() Па и
Па и ![]() Па и высотой, равной
Па и высотой, равной ![]() м. Строим эпюру избыточного давления на участке MN.
м. Строим эпюру избыточного давления на участке MN.
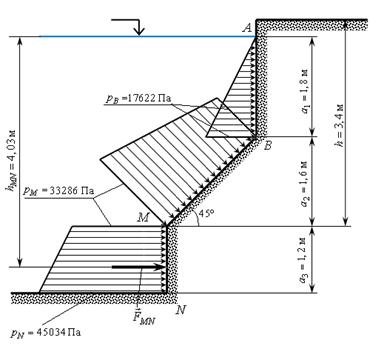
Рис.1. Расчетная схема к задаче 1 и эпюра избыточного давления.
3. Силу избыточного давления на указанную участок MN смоченной поверхности определим с помощью формулы [1, с.30]
![]() ,
,
где![]() - площадь соответствующей эпюры давления;
- площадь соответствующей эпюры давления;
![]() - ширина стенки.
- ширина стенки.
Площадь эпюры давления ![]() определяем по формуле площади трапеции
определяем по формуле площади трапеции
![]() .
.
Тогда искомая сила будет равна
![]() Н
Н![]() кН.
кН.
При этом высоту точки приложения этой силы от поверхности воды можно определить по формуле [1, с.32]
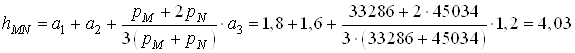 м.
м.
Ответ: ![]() Па;
Па; ![]() Па;
Па;
![]() кН.
кН.
Задача 2
Для подачи воды из резервуара, в котором поддерживается постоянный уровень, предусмотрен короткий трубопровод, состоящий из труб разного диаметра, соединенных последовательно (рис.2.1 и 2.2). Над горизонтом воды в резервуаре поддерживается внешнее давление ![]() .
.
Требуется:
1. Выяснить режим движения на каждом участке короткого трубопровода.
2. Определить напор ![]() с учетом режима движения. В случае турбулентного режима движения для определения коэффициента
с учетом режима движения. В случае турбулентного режима движения для определения коэффициента ![]() использовать универсальную формулу А.Д. Альтшуля, справедливую для всех зон сопротивления этого режима, формула имеет вид
использовать универсальную формулу А.Д. Альтшуля, справедливую для всех зон сопротивления этого режима, формула имеет вид
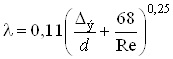 .
.
Высота эквивалентной шероховатости ![]() для технических труб задана в таблице исходных данных.
для технических труб задана в таблице исходных данных.
Расчет выполнить для одного из вариантов по данным, приведенным в табл.2.1 и 2.2.
Исходные данные:
| Исходные данные | Последняя цифра номера зачетной книжки | Исходные данные | Предпоследняя цифра номера зачетной книжки |
| 3 | 1 | ||
| Расход | 10 | Длина, | 150 |
| Внешнее давление | 1,05 | Длина, | 100 |
| Диаметр | 75 | Эквивалентная шероховатость | 0,45 |
| Диаметр | 100 | Температура воды | 13 |
| Номер рисунка | 2.2 | Номер рисунка | 2.2 |
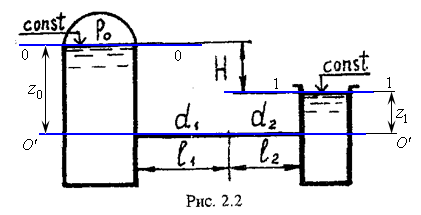
Рис.2. Расчетная схема к задаче 2
Решение:
Рассмотрим установившееся движение воды в заданном трубопроводе (рис.2).
1. Составляем уравнение Бернулли в общем виде для сечений 0-0 и 1-1 (сечение 0-0 совпадает со свободной поверхностью воды в левом резервуаре, сечение 1-1 - со свободной поверхностью правого резервуара):
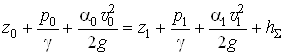 , (1)
, (1)
где ![]() и
и ![]() - расстояние от произвольно выбранной горизонтальной плоскости сравнения до центра тяжести живых сечений 0 и 1;
- расстояние от произвольно выбранной горизонтальной плоскости сравнения до центра тяжести живых сечений 0 и 1;
![]() и
и ![]() - давление в центрах тяжести живых сечений 0 и 1;
- давление в центрах тяжести живых сечений 0 и 1;
![]() и
и ![]() - средняя скорость движения жидкости в живых сечениях 0 и 1;
- средняя скорость движения жидкости в живых сечениях 0 и 1;
![]() и
и ![]() - коэффициент Кориолиса. Для турбулентного режима движения жидкости
- коэффициент Кориолиса. Для турбулентного режима движения жидкости ![]() ;
;
![]() - суммарные потери напора на преодоление сил сопротивления при движении потока в заданном трубопроводе;
- суммарные потери напора на преодоление сил сопротивления при движении потока в заданном трубопроводе;
![]() - удельный вес жидкости. Для воды при
- удельный вес жидкости. Для воды при ![]() принимаем
принимаем ![]() Н/м3 [1, табл.1.2].
Н/м3 [1, табл.1.2].
2. Намечаем горизонтальную плоскость сравнения. В качестве таковой берем плоскость ![]() , совпадающей с осью трубопровода.
, совпадающей с осью трубопровода.
Выясняем значения отдельных членов, входящих в уравнение (1) относительно плоскости сравнения ![]() :
:
![]() ;
; ![]() (расчет производим для избыточного давления);
(расчет производим для избыточного давления);
![]() . (2)
. (2)
3. Подставляя (2) в (1), получаем расчетное уравнение для определения искомой величины ![]() :
:
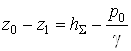
Или 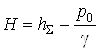 . (3)
. (3)
4. Определяем скорость движения воды в трубопроводе:
на участке ![]()
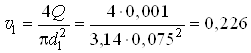 м/с;
м/с;
на участке ![]()
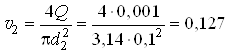 м/с.
м/с.
Похожие работы
... критерий гидродинамического подобия; Л. Прандтль (1875—1953), разработавший теорию турбулентных потоков. Не остались в стороне от развития технической гидравлики и ученые России. Инженерное направление в гидромеханике интенсивно разрабатывалось в стенах Петербургского института путей сообщения, где была создана первая в России гидравлическая лаборатория и плодотворно работала группа ученых под ...
... до так называемой ватерлинии. Поскольку внутри корпуса корабля много пространства, заполненного воздухом, средняя удельная масса судна меньше плотности воды и выталкивающая сила удерживает его на плаву. Закон Архимеда объясняет также, почему воздушный шар, заполненный тёплым воздухом или газом, который легче воздуха (водородом, гелием), улетает ввысь. Знание гидравлики позволило Архимеду ...
... от поверхности Земли, где атмосфера разрежена и почти не влияет на движение ИСЗ, ракета делает поворот и сообщает ИСЗ первую космическую скорость в направлении, перпендикулярном вертикали. Законы сохранения в механике Импульс тела. По 2-му закону Ньютона изменение скорости тела возможно только в результате его взаимодействия с другими телами, т.е. при действии силы. Пусть на тело массой m в ...
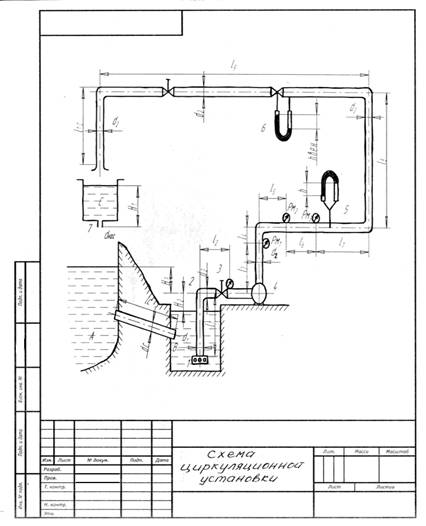
... 30 μвен 0,94 hвен, мм рт. ст 166 2, кг/м3 0 РВ, кПа 40 Рм1, кПа 145 dнас, мм 30 μнас 0,82 3. Схема установки 4. Расчет циркуляционной установки 4.1 Определение геометрической высоты всасывания насоса Н2 Для определения геометрической высоты воспользуемся известным уравнением Бернулли. Для его применения необходимо ...
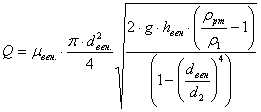
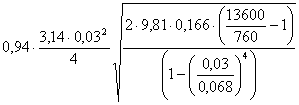
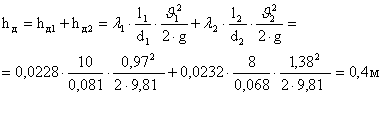
0 комментариев