Навигация
Определяем режим движения воды на участках трубопровода. Для этого вычисляем число Рейнольдса по формуле
5. Определяем режим движения воды на участках трубопровода. Для этого вычисляем число Рейнольдса по формуле
![]() ,
,
где ![]() м2/с - коэффициент кинематической вязкости воды при
м2/с - коэффициент кинематической вязкости воды при ![]() °С [1, табл.1.13].
°С [1, табл.1.13].
Тогда будем иметь:
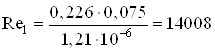 ;
;
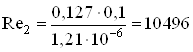 .
.
Поскольку имеем ![]() и
и ![]() , где для круглых труб критическое число Рейнольдса
, где для круглых труб критическое число Рейнольдса ![]() , то режим движения воды в трубопроводе - турбулентный.
, то режим движения воды в трубопроводе - турбулентный.
6. Определяем потери напора ![]() . Имеем
. Имеем
![]() . (4)
. (4)
где ![]() - потери напора по длине трубопровода;
- потери напора по длине трубопровода;
![]() - местные потери при перемещении воды в системе.
- местные потери при перемещении воды в системе.
Суммарные потери по длине трубопровода равны сумме потерь на каждом из участков, то есть
![]() . (5)
. (5)
Потери по длине на каждом участке определяем по формуле Дарси
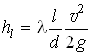 , (6)
, (6)
где ![]() - коэффициент гидравлического трения.
- коэффициент гидравлического трения.
Для определения коэффициента ![]() используем универсальную формулу А.Д. Альтшуля, справедливую для всех зон сопротивления турбулентного режима
используем универсальную формулу А.Д. Альтшуля, справедливую для всех зон сопротивления турбулентного режима
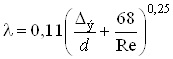 .
.
Имеем
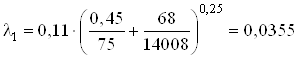 ;
;
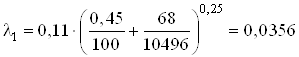 .
.
Находим потери по длине
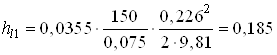 м;
м;
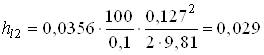 м;
м;
![]() м.
м.
Потери напора в местных сопротивлениях вычисляем по формуле Вейсбаха
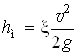 , (6)
, (6)
где ![]() - средняя скорость за данным сопротивлением;
- средняя скорость за данным сопротивлением; ![]() - коэффициент местного сопротивления.
- коэффициент местного сопротивления.
Находим потери на вход в трубопровод
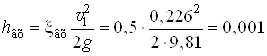 м,
м,
где![]() - коэффициент сопротивления при входе в трубопровод, считая, что вход прямой, заделанный заподлицо в стенку [1, с.83].
- коэффициент сопротивления при входе в трубопровод, считая, что вход прямой, заделанный заподлицо в стенку [1, с.83].
Находим потери при внезапном расширении трубопровода с диаметра ![]() до диаметра
до диаметра ![]() . При этом для определения потерь воспользуемся формулой Борда [1, с.85]
. При этом для определения потерь воспользуемся формулой Борда [1, с.85]
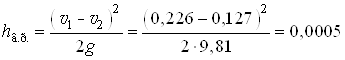 м.
м.
Определяем потери при выходе воды из трубы в правый резервуар под уровень
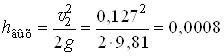 м.
м.
Определяем суммарные местные потери
![]() м.
м.
Находим суммарные потери напора в трубопроводе
![]() м.
м.
7. Используя уравнение (3), вычисляем необходимый напор
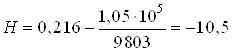 м.
м.
Знак минус свидетельствует о том, что уровень воды в правом резервуаре расположен выше уровня воды в левом резервуаре.
Ответ: ![]() м.
м.
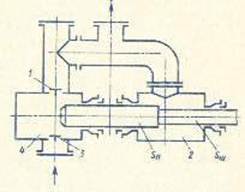
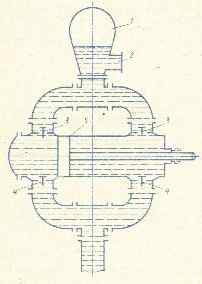
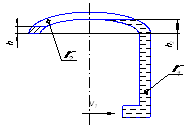
На рис.3.1 и 3.2 показаны резервуары, в оболочке которых сделаны круглые отверстия, к которым присоединены внешние цилиндрические насадки диаметром ![]() Отметки уровня воды в резервуарах, центра отверстий, дна указаны в табл.3.1 и 3.2.
Отметки уровня воды в резервуарах, центра отверстий, дна указаны в табл.3.1 и 3.2.
Скорость в резервуарах ![]() . Отметка уровня воды держится постоянной. Длину насадка принять равной
. Отметка уровня воды держится постоянной. Длину насадка принять равной ![]() .
.
Требуется:
1. Определить расход ![]() , вытекающий через внешний цилиндрический насадок.
, вытекающий через внешний цилиндрический насадок.
2. Определить скорость в сжатом сечении насадка ![]() .
.
Расчеты выполнить для одного из вариантов по данным, приведенным в табл.3.1 и 3.2.
Исходные данные:
| Исходные данные | Последняя цифра номера зачетной книжки | Исходные данные | Предпоследняя цифра номера зачетной книжки |
| 3 | 1 | ||
| Внешнее давление | 1,09 | Отметка А, м | 10 |
| Диаметр | 7 |
| 7,6 |
| Температура воды | 19 |
| 7,6 |
| Номер рисунка | 3.2 |
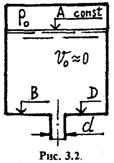
Рис.3. Расчетная схема к задаче 3
Решение:
Определяем расчетный напор, используя формулу 6.4 [1, с.101]
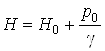 ,
,
где![]() - напор над центром насадка;
- напор над центром насадка;
![]() - избыточное давление на поверхности воды в резервуаре;
- избыточное давление на поверхности воды в резервуаре;
![]() Н/м3 - удельный вес воды при
Н/м3 - удельный вес воды при ![]() С [1, табл.1.2].
С [1, табл.1.2].
Имеем:
![]() м.
м.
 м.
м.
Далее находим число Рейнольдса по формуле [1, с.106]
![]() ,
,
где![]() м2/с - кинематическая вязкость воды при
м2/с - кинематическая вязкость воды при ![]() С [1, табл.1.13].
С [1, табл.1.13].
Тогда получим
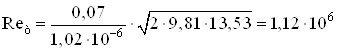 .
.
Определяем коэффициент расхода внешнего цилиндрического насадка, используя эмпирическую формулу [1, с.106]
 .
.
Определяем расход ![]() , вытекающий через внешний цилиндрический насадок по формуле [1, с.104]
, вытекающий через внешний цилиндрический насадок по формуле [1, с.104]
![]() ,
,
где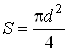 - площадь выходного сечения.
- площадь выходного сечения.
Таким образом, получаем
 м3/с.
м3/с.
Скорость в сжатом сечении насадка ![]() определим по формуле [1, с.104]
определим по формуле [1, с.104]
![]() ,
,
где![]() - коэффициент скорости. Для внешнего цилиндрического насадка
- коэффициент скорости. Для внешнего цилиндрического насадка
![]()
где![]() - коэффициент сжатия для внешнего цилиндрического насадка.
- коэффициент сжатия для внешнего цилиндрического насадка.
Тогда ![]() и находим
и находим
![]() м/с
м/с
Ответ: ![]() м3/с;
м3/с; ![]() м/с.
м/с.
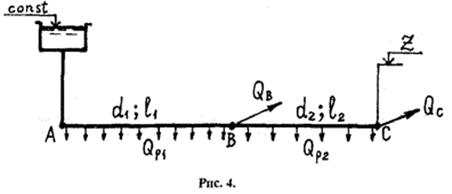
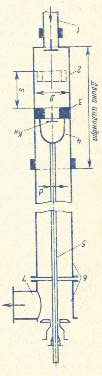
Из напорного бака с постоянным уровнем вода подается потребителям по трубопроводу, состоящему из двух последовательно соединенных участков гидравлически длинных труб (рис.4).
Требуется:
1. Определить расчетный расход на каждом участке.
2. Определить потери напора на каждом участке, пользуясь таблицами для гидравлически длинных труб.
3. Определить отметку воды в напорном баке.
Расчеты выполнить для одного из вариантов по данным, приведенным в табл.4.1 и 4.2.
Исходные данные:
| Исходные данные | Последняя цифра номера зачетной книжки | Исходные данные | Предпоследняя цифра номера зачетной книжки |
| 3 | 1 | ||
| Расход | 50 | Длина | 480 |
| Расход | 0 | Длина | 500 |
| Расход | 20 | Отметка пьезометрической линии в конце системы | 0 |
| Диаметр | 200 | ||
| Диаметр | 150 | Вид трубы | новые стальные |
Решение:
Выполняем схему трубопровода согласно исходным данным (рис.4)

Рис.4. Расчетная схема к задаче 4
1. Поскольку участки трубопровода 1 (AB) и 2 (BC) соединены последовательно, то имеем
![]() ,
,
где ![]() - расчетный расход на первом участке;
- расчетный расход на первом участке;
![]() - расчетный расход на втором участке.
- расчетный расход на втором участке.
Расчетный расход на втором участке определяем по формуле 8.26 [1, с.131]
избыточное давление эпюра трубопровод
 ;
;
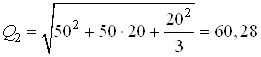 л/с.
л/с.
Таким образом,
![]() л/с.
л/с.
2. Потери напора на каждом участке определим по формуле 8.25 [1, c.131]
![]() ,
,
где![]() - длина участка;
- длина участка;
![]() - расходная характеристика трубопровода;
- расходная характеристика трубопровода;
![]() - расчетный расход на данном участке трубопровода.
- расчетный расход на данном участке трубопровода.
Для первого участка имеем ![]() м,
м, ![]() мм,
мм, ![]() л/с (табл.8.1 [1, с.116]) для новых труб. Тогда
л/с (табл.8.1 [1, с.116]) для новых труб. Тогда
![]() м.
м.
Аналогично для второго участка получаем: ![]() м,
м, ![]() мм,
мм, ![]() л/с
л/с
![]() м.
м.
3. Определяем отметку воды в напорном баке. Поскольку по условию ![]() , то отметка в напорном баке будет равна сумме гидравлических потерь, то есть
, то отметка в напорном баке будет равна сумме гидравлических потерь, то есть
![]() м.
м.
Ответ: ![]() л/с;
л/с; ![]() м;
м; ![]() м;
м;
![]() м.
м.
Список использованной литературы
1. Некрасов Б.Б. Справочное пособие по гидравлике, гидромашинам и гидроприводам. Мн.: Высшая школа, 1985.
2. Альтшуль А.Д. Примеры расчетов по гидравлике. М.: Стройиздат, 1977.
Похожие работы
... критерий гидродинамического подобия; Л. Прандтль (1875—1953), разработавший теорию турбулентных потоков. Не остались в стороне от развития технической гидравлики и ученые России. Инженерное направление в гидромеханике интенсивно разрабатывалось в стенах Петербургского института путей сообщения, где была создана первая в России гидравлическая лаборатория и плодотворно работала группа ученых под ...
... до так называемой ватерлинии. Поскольку внутри корпуса корабля много пространства, заполненного воздухом, средняя удельная масса судна меньше плотности воды и выталкивающая сила удерживает его на плаву. Закон Архимеда объясняет также, почему воздушный шар, заполненный тёплым воздухом или газом, который легче воздуха (водородом, гелием), улетает ввысь. Знание гидравлики позволило Архимеду ...
... от поверхности Земли, где атмосфера разрежена и почти не влияет на движение ИСЗ, ракета делает поворот и сообщает ИСЗ первую космическую скорость в направлении, перпендикулярном вертикали. Законы сохранения в механике Импульс тела. По 2-му закону Ньютона изменение скорости тела возможно только в результате его взаимодействия с другими телами, т.е. при действии силы. Пусть на тело массой m в ...
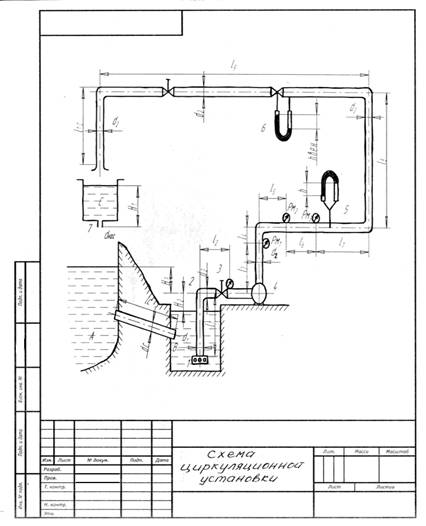
... 30 μвен 0,94 hвен, мм рт. ст 166 2, кг/м3 0 РВ, кПа 40 Рм1, кПа 145 dнас, мм 30 μнас 0,82 3. Схема установки 4. Расчет циркуляционной установки 4.1 Определение геометрической высоты всасывания насоса Н2 Для определения геометрической высоты воспользуемся известным уравнением Бернулли. Для его применения необходимо ...
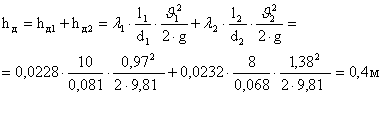
0 комментариев