Класичний метод аналiзу перехiдних процесiв. Вимушений i вiльний режими

3. Класичний метод аналiзу перехiдних процесiв. Вимушений i вiльний режими

Аналiз електричних процесiв в ЛЕК, як вiдомо, базується на розв'язаннi рiвнянь Кiрхгофа для миттєвих значень напруг i струмiв в елементах кола. Цi рiвняння приводяться до лiнiйного неоднорiдного диференцiйного рiвняння з постiйними коефiцiєнтами.

У загальному виглядi процеси в ЛЕК описуються лiнiйним диференцiйним рiвнянням n-го порядку:

, (1)

де  - шукана функцiя;  - вiдома функцiя, яка залежить вiд зовнiшньої дiї;  - постiйнi коефiцiєнти.

В математицi існують рiзнi способи розв'язання рiвняння (1). Згiдно з класичним методом розв'язок (1) слiд шукати у виглядi суми двох функцiй:

, (2)

де 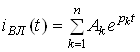 - загальний розв'язок (1), який характеризує електричнi явища за вiдсутнiстю зовнiшньої дiї (). Якщо , то коло знаходиться в режимi власних (вiльних) коливань. Функцiї, що визначаються за загальним розв'язком, звуться вiльними складовими (струмiв, напруг тощо). В (2)  - частинний розв'язок, що характеризує вимушений режим, який обумовлений зовнiшнiм джерелом. Якщо  - постiйна функцiя або перiодична за часом, то вимушений струм (напруга) буде одночасно i усталеним.

Iснує унiверсальний метод визначення вiльної складової, згiдно з яким оператор диференцiювання в (1) замiнюють алгебраїчним оператором p:

; ... ; ; .

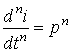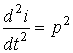Пiсля цiєї замiни отримуємо характеристичне рiвняння кола:

. (3)

Степiнь характеристичного полiнома визначається порядком диференцiйного рiвняння (3) i зветься порядком кола.

Розв'язуючи (3), визначають коренi характеристичного рiвняння  (k =1,2,..., n). За знайденими коренями знаходять шуканий розв'язок

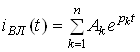, (4)

де  - сталi iнтегрування, якi обчислюються за початковими умовами.

Для знаходження сталих iнтегрування вираз (4), а також початковi умови ,  пiдставляють до (2) i розв'язують здобуте рiвняння чи систему рiвнянь. Наприклад, для кола першого порядку маємо , звiдки .

Слiд пам'ятати, що фiзично iснують тiльки повнi струми (напруги), якi дорiвнюють сумi вимушеної та вiльної складової. Саме їх можна вимiряти або спостерiгати за допомогою приладiв (осцилографа, вольтметра тощо). Щодо них слушнi закони комутацiї. Вимушена та вiльна складовi є розрахунковими величинами, сума яких дає реальнi (фiзичнi) струми i напруги.

4. Перехідні процеси в колах RL і RC

4.1 Режим вiльних коливань у колi RC

Розв'яжемо задачу аналiзу коливань в RC колi, схема якого зображена на рис.1а, за початкової умови . Спади напруг на ємностi  та на опорi 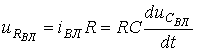 задовольняють другому закону Кiрхгофа, згiдно з яким

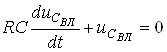, або . (5)

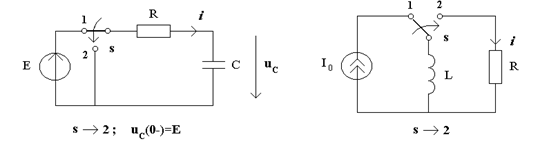
а) б)

Рисунок 1

Диференцiйному рiвнянню (5) вiдповiдає характеристичне: . Це рiвняння має єдиний корiнь , який є дiйсним вiд'ємним числом. Iнакше, , де стала  має вимiрнiсть часу. Вона зветься сталою часу кола ([t] = [RC] = Ом´Ф = Ом´А´с/В = с).

Отже, загальний розв'язок рiвняння (5) такий:

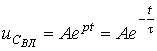. (6)

Коефiцiєнт A розраховується з початкових умов з використанням закону комутацiї. За формулою (6) ; згiдно з законом комутацiї за ненульових початкових умов . Тобто A = E, i (6) приймає вигляд .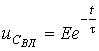

Знайдемо струм у колi та спад напруги на опорi:

; , де .

Вiдповiднi графiки зображено на рис.2а. З рисунку видно, що згiдно з другим законом Кiрхгофа, в будь-який момент часу алгебраїчна сума спадiв напруг у колi дорiвнює нулю. Розглянемо змiст сталої часу. Якщо , то ; . Отже, стала часу t дорівнює інтервалу часу, за який напруга i струм в колi RC зменшуються за абсолютною величиною в режимi вiльних коливань у e = 2,72 разiв.

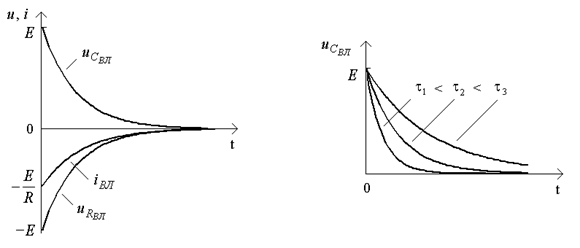
а) б)

Рисунок 2

Стала часу електричного кола - величина, що характеризує електричне коло з одним iнерцiйним елементом (iндуктивнiстю чи ємнiстю) i дорiвнює довжинi пiддотичної до кривої вiльної складової перехiдного струму. Дiйсно, . Графiк функцiї  зображено на рис.2б, а чисельнi значення наведено у таблицi 2.

Таблиця 2

Iз знайдених рiшень виходить, що процес зменшування напруги та струму продовжується нескiнченно, але практично вiльнi коливання вважають закiнченими при , коли  або при , коли . Вважатимемо, що тривалiсть перехiдного процесу становить .

Для наочного уявлення про характер перехiдних процесiв у ЛЕК прийнято коренi характеристичного рiвняння зображати точками на комплекснiй площинi.