Граница двух различных металлов

1. Граница двух различных металлов.

При установлении равновесия на этой границе происходит выравнивание электрохимических потенциалов электронов в металлах М₁ и М₂.

Условие равновесия имеет вид

 (1.1.13)

 (1.1.14)

Отсюда для гальвани-потенциала на границе металл – металл получают выражение:

 (1.1.15)

Таким образом, в условиях равновесия работа перенесения электрона из одного металла в другой равна нулю, но работа переноса единицы воображаемого заряда, т. е. , отлична от нуля, поскольку химические потенциалы электрона в различных металлах неодинаковы.

2. Граница металла М с раствором, содержащим ионы этого же металла. При установлении равновесия происходит выравнивание электрохимических потенциалов ионов M^z+ в растворе и в кристаллической решетке металла.

При равновесии:

 (1.1.16)

 (1.1.17)

Гальвани-потенциал на границе металл – раствор соответствующей соли имеет вид:

 (1.1.18)

Поскольку , а , уравнение (1.1.18) можно переписать в виде:

 (1.1.19)

Уравнение (1.1.19) – это частный случай уравнения Нернста для отдельного гальвани-потенциала. Таким образом, в условиях рассмотренного электрохимического равновесия работа перенесения иона M^z+ из металла в раствор или обратно равна нулю. Гальвани-петенциал  зависит от концентрации потенциалопределяющих ионов M^z+ и также может быть сведен к нулю. Однако невозможность измерить гальвани-потенциал не позволяет установить, при какой именно концентрации M^z+=0.

Правильно разомкнутая электрохимическая цепь, на концах которой можно измерить электрическую разность потенциалов, всегда должна заканчиваться одинаковыми по своему химическому составу металлами. Электрохимическая цепь является равновесной при условии, что электрохимическое равновесие наблюдается на каждой фазовой границе, а разность потенциалов на концах цепи Е скомпенсирована разностью потенциалов от внешнего источника цепи.

Из (1.1.5):

E=–ΔG/nF (1.1.20)

Т.е. разность потенциалов на концах равновесной электрохимической цепи однозначно связана с изменением свободной энергии Гиббса в ходе соответствующей химической реакции. Величина E и называется ЭДС, т.е. электродвижущей силой электрохимической цепи. Уравнение (1.1.20) применимо только в том случае, если на всех фазовых границах устанавливается равновесие, в противном случае разность потенциалов на концах цепи не равна ЭДС и уравнение оказывается неприменимым [2].

1.2 Классификация электродов. Классификация электрохимических цепей

 

Классификация электродов

Классификация электродов проводится по химической природе веществ Ox и Red, участвующих в электродном процессе.

Электродом 1-ого рода называют систему, в которой восстановленной формой является металл электрода, а окисленной формой – простые или комплексные ионы этого же металла.

Примером может служить система Cu²⁺+2e^-=Cu, для которой:

 (1.2.1)

Как правило, электроды 1-ого рода обратимы по катиону, т.е. их потенциал является функцией активности катиона. Однако, есть небольшое количество электродов 1-ого рода, обратимых по аниону, например 2Te+2e^-=, для которого

 

 (1.2.2)

К электродам 1-ого рода относятся амальгамные электроды, в которых восстановленной формой служит амальгама какого-либо металла, а окисленной – ионы того же металла:

Tl⁺+e^-(Hg)=Tl(Hg)

Поскольку в таких системах может изменяться концентрация как Ox, так и Red, то

 (1.2.3)

Здесь  - активность таллия в амальгаме.

Общая формула для потенциала электрода 1-ого рода имеет вид:

 (1.2.4)

Здесь - активность потенциалопределяющих ионов в растворе, - зарядовое число потенциалопределяющих ионов с учетом знака; - активность соответствующего металла. Для чистых металлов =const и соответствующий член  вводится в стандартный потенциал.

Электродом 2-ого рода называют систему, в которой металл покрыт слоем его труднорастворимой соли (или оксида), а раствор содержит анионы этой соли (для оксида – ионы OH^-):

Таким образом, окисленной формой здесь является труднорастворимая соль , а восстановленная форма представлена металлом  и анионом . Потенциал электрода 2-ого рода определяется активность ионов соответствующего металла , которую можно выразить через произведение растворимости соли L_s и активность аниона . Таким образом, уравнение Нернста для электродов 2-ого рода принимает вид:

 (1.2.5)

Здесь - стандартный потенциал системы М^z+/М; - стандартный потенциал электрода 2-ого рода. Как следует из уравнения (1.2.5), электрод 2-ого рода является обратимым по аниону.

Рассмотрим некоторые примеры электродов 2-ого рода.

Хлорсеребряный электрод: AgCl+e^-=Ag+Cl^-

 (1.2.6)

Каломельный электрод: Hg₂Cl₂+2e^-=2Hg+2Cl^-

 (1.2.7)

Ртутно-оксидный электрод: Hg₂O+2e^-+H₂O=2Hg+2OH^-

 (1.2.8)

Во всех системах, отвечающих электродам 1 и 2-ого, одним из компонентов восстановленной формы служит металл электрода. Если же инертный металл электрода не участвует в полуреакциях, а является только передатчиком электронов между Ox и Red, то такие системы называют окислительно-восстановительными электродами или редокс-системами.

Например, система:

Fe³⁺+e^-=Fe²⁺,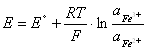

Cu²⁺+e^-=Cu⁺,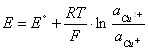

С платиновым электродом в качестве инертного переносчика электронов между Ox и Red.

Среди окислительно-восстановительных электродов выделяют газовые электроды. Газовый электрод состоит инертного металла (часто платины или платинированной платины), к которому подводится электрохимически активный газ. Молекулы газа адсорбируются на поверхности металла, распадаясь при этом на атомы, а адсорбированные атомы участвуют уже непосредственно в электродной реакции. Поскольку между молекулами газовой фазы и адсорбированными атомами устанавливается равновесие, то при записи электродного равновесия промежуточное адсорбционное состояние часто опускают. Примером газового электрода, обратимого по катиону, является водородный электрод, на поверхности которого устанавливается равновесие: H⁺+e^-=¹/₂H₂.

Потенциал водородного электрода – это ЭДС цепи:

Pt, H₂(p=1)│H₃O⁺(=1) ¦¦ H₃O⁺()│ H₂(p), Pt

Если в правой части цепи положить =1 и , то цепь окажется полностью симметричной и ее ЭДС должна равняться нулю. Следовательно,

 (1.2.9)

Классификация электрохимических цепей.

Электрохимические цепи обычно классифицируют по двум признакам:

1)  по источнику электрической энергии

2)  по наличию или отсутствию в цепи границы двух различных растворов: соответственно цепи с переносом и без переноса.

В физических цепях источником электрической энергии служит различие в физическом состоянии двух одинаковых по своему химическому составу электродов. Эти электроды погружены в один и тот же раствор и при работе цепи электрод, находящийся в менее устойчивом состоянии, переходит в более устойчивое состояние.

Физические цепи – цепи без переноса – подразделяются на аллотропические и гравитационные.

Аллотропические цепи – это цепи, в которых менее устойчивое состояние одного электрода обусловлено тем, что он изготовлен из метастабильной модификации данного металла.

Гравитационные цепи были впервые реализованы русским электрохимиком Р. А. Колли (1875). Например, гравитационная цепь, состоящая из двух ртутных электродов в растворе Hg₂(NO₃)₂. Ее левый электрод с более высоким уровнем ртути обладает большим запасом потенциальной энергии по сравнению с правым электродом. Этот избыток потенциальной энергии в расчете на 1 г-экв металлической ртути составляет , где  - молекулярная масса ртути;  - ускорение силы тяжести;  - разность уровней ртути. При работе цепи на левом электроде происходит растворение ртути;

Hg→Hg+e^-

а на правом, наоборот, разряд ионов Hg:

Hg+e^- →Hg

В результате этих двух электродных процессов происходит перенос металлической ртути из левой части в правую, который направлен на выравнивание уровней ртути. При этом перенос 1 г-экв ртути соответствует прохождению через систему 1 фарадея и электрической работе EF. Поскольку источником этой энергии является потенциальная энергия , то ЭДС гравитационной цепи равна:

 (1.2.10)

Из-за малых величин Е гравитационные цепи не имеют практического значения. Они представляют интерес как пример, иллюстрирующий законы превращения энергии.

В концентрационных цепях оба электрода идентичны как по физическому состоянию, так и по химической природе участников окислительно-восстановительных процессов; они отличаются только концентрацией компонентов Ox или Red. Источником электрической энергии является разность свободных энергий Гиббса, обусловленная различными активностями одних и тех же химических компонентов. Концентрационные цепи можно приготовить из амальгам разных концентраций в одном и том же растворе; из одинаковых электродов 1 или 2-ого рода, находящихся в растворах разной концентрации; из одинаковых газовых электродов, работающих при разных давлениях газов.

Различают концентрационные цепи без переноса, т.е. без границы двух растворов, и с переносом, когда имеется такая граница. Цепи, построенные из двух амальгамных электродов с разной концентрацией амальгам или из двух газовых электродов с разным давлением газа, содержат всего один раствор, а потому представляют собой цепи без переноса. В этих цепях на электроде с большей концентрацией амальгамы или с большим давлением газа происходит ионизация атомов амальгамы или газа, а на электроде с меньшей концентрацией амальгамы (с меньшим давлением газа) идут обратные процессы образования амальгамы или газа. Таким образом, в результате работы концентрационной цепи происходит выравнивание активностей компонентов на обоих электродах. В качестве примера можно рассмотреть следующую амальгамную цепь:

Pt│Zn (Hg)│ZnSO₄│Zn (Hg)│Pt

 _{a1 a2}

На обеих границах раздела металл – раствор идут процессы

Zn²⁺+2e^-(Hg)=Zn (Hg)

Условие равновесия на левом электроде

 (1.2.11)

или

 (1.2.12)

откуда

 (1.2.13)

Из аналогичного равновесия на правом электроде получаем

 (1.2.14)

На границах платины с амальгамами наблюдаются равновесия

e^- (Pt)=e^- (Ам₁) и e^- (Ам₂)= e^- (Pt)

Из условий равновесия и легко получить выражения для гальвани-потенциалов на этих двух границах:

 и

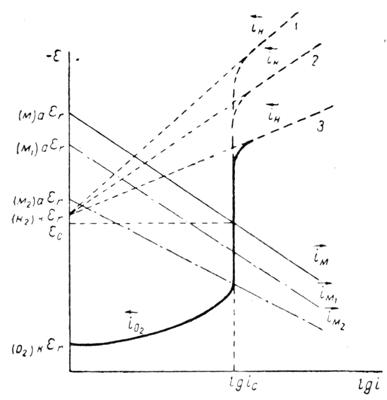
электрохимический потенциал равновесие пурбе

Так как изменение состава амальгамы приводит к изменению химического потенциала электрода (т.е. ), то . Суммируя все гальвани-потенциалы в рассматриваемой цепи, получаем для ЭДС следующее простое выражение:

 (1.2.15)

Рассмотрим теперь концентрационные цепи, которые содержат два раствора одинакового состава, но различной концентрации. Цепь с переносом можно построить следующим образом:

М│М_υ+ А_υ-¦ М_υ+ А_υ-│М

 _{as(1) as(2)}

где оба электрода 1-ого рода обратимы по катионам М^z+. Из условия равновесия по левой границе

 или  (1.2.16)

получаем для гальвани-потенциала :

 (1.2.17)

Аналогично для гальвани-потенциала на правой границе имеем

 (1.2.18)

Сумма этих гальвани-потенциалов равна

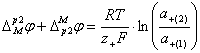 (1.2.19)

Чтобы получить разность потенциалов на концах цепи, к сумме гальвани-потенциалов  нужно прибавить диффузионный потенциал на границе двух растворов .

Для рассматриваемой системы:

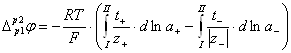 (1.2.20)

Если предположить, что концентрации двух растворов отличаются не очень сильно или оба раствора достаточно разбавлены и, следовательно, можно принять постоянство чисел переноса в переходной зоне на границе двух растворов, то из уравнения (1.2.20) находим

 (1.2.21)

Складывая уравнения (1.2.19) и (1.2.21) и заменяя при этом z₊=n/υ₊ и │z _-│=n/υ_- получаем для разности потенциалов на концах цепи:

 (1.2.22)

где  - активность соли;  - средняя активность.

При работе цепи, когда >, Е>0, следовательно, на правом электроде идет катодный процесс выделения металла. Если через цепь прошел 1 фарадей электричества, то за счет электролиза из правого раствора будет удален 1 г-экв катионов. Но через границу двух растворов в правую часть цепи перейдет t₊ г-экв катионов, так что суммарная убыль катионов из правого раствора составит 1– t₊= t_- г-экв. Одновременно из правого раствора в левый перейдет t_- г-экв анионов. Таким образом, прохождение через цепь 1 фарадея сопровождается убылью t_- г-экв соли из правого раствора. Аналогичный анализ процессов в левой части цепи показывает, что при прохождении через цепь 1 фарадея здесь возникает t_- г-экв соли. Следовательно, работа концентрационной цепи с переносом сопровождается выравниванием концентраций в обоих растворах. Данный вывод оказывается справедливым и при условии <, но при этом все процессы в цепи протекают в обратном направлении.

В химических цепях источником электрической энергии является свободная энергия химической реакции, протекающей в электрохимической системе.

В химических цепях без переноса один из электродов должен быть обратимым по катиону, а другой – по аниону.

Примеры:

амальгамный электрод – электрод 2-ого рода:

Ag│K(Hg)│KCl│AgCl, Ag

газовый электрод – электрод 2-ого рода:

обратимый по катионам

Pt, H₂│HCl│Hg₂Cl₂, Hg│Pt

обратимый по анионам

Pt, H₂│HCl│Cl₂, Pt

электрод 1-ого рода – газовый электрод:

Zn│ZnCl₂│Cl₂, Pt│Zn

Среди различных химических цепей без переноса большое значение имеет цепь

Pt│Cd(Hg)│CdSO₄ (насыщенный раствор)│Hg₂SO₄, Hg│Pt

лежащая в основе стандартного элемента Вестона. ЭДС этого элемента отличается большой стабильностью и малым температурным коэффициентом, а потому он используется в качестве стандарта при потенциометрических измерениях.

Однако подавляющее большинство химических цепей – это цепи с переносом, в которых растворы соединены или непосредственно, или через солевой мостик. Комбинируя различные окислительно-восстановительные полуреакции, можно построить очень большое число химических цепей. Разность соответствующих стандартных потенциалов позволяет в первом приближении оценить ЭДС этих цепей. Точное значение разности потенциалов на концах химической цепи в переносом рассчитать не удается, во-первых, из-за невозможности точного определения диффузионного потенциала и, во-вторых, из-за неизбежной замены активностей отдельных ионов в формуле Нернста средними активностями или прсото концентрациями этих ионов.

Пример химической цепи с переносом: элемент Даниэля – Якоби:

Cu│Zn│ZnSO₄¦CuSO₄│Cu

Разность потенциалов на концах этой цепи равна

 (1.2.23)