Алгоритм рішення системи нелінійних рівнянь методом Ньютона

2 Алгоритм рішення системи нелінійних рівнянь методом Ньютона.

Запишемо рівняння (17) у векторно-матричній формі

, (8)

де  - вектор комплексних амплітуд струму комплексних амплітуд напруги;

 - вектор нелінійного опору;

 - вектор комплексних амплітуд заряду нелінійної ємності;

 - вектор складової джерела струму;

 та  - квадратні діагональні матриці. Розмірність векторів та матриць дорівнює 2N+1.

Ліва частина формули (7), виявляється трансцендентною векторною функцією, аргумент якої – вектор напруги

. (9)

За допомогою формули (7) отримаємо співвідношення для методу Ньютона стосовно (9)

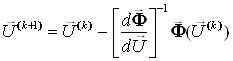. (10)

Верхній індекс вектора напруги вказує на номер ітерації.

Якщо в (9) підставити , то в лівій частині не отримаємо нуль. Тому вектор – функцію  називають незв’язною.

Продиференцюємо (10) по вектору

. (11)

Нагадаємо, що похідна від вектор-функції незв’язності за векторним аргументом виявляється матрицею Якобі. Як видно, вона складається з трьох складових. Позначимо  і  елементи матриць  та .Тоді

, , .

В даному випадку використання методу Ньютона особливо ефективне, оскільки вдається отримати аналітичний вираз для  і . Покажемо, як знаходиться, наприклад, .

За визначенням

.

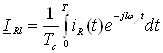Величину  запишемо у вигляді

.

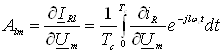В свою чергу ,

.

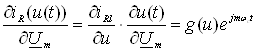Похідна від струму  за напругою u(t) позначена як провідність . Приватна похідна від напруги за комплексною ампліту-

дою  отримана за допомогою (11).Це дозволяє записати

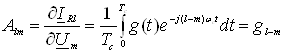, (12)

де  - (l-m) – а гармоніка похідної .

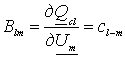, (13)

де  -а гармоніка похідної , яка уявляє собою диференційну ємність.

Опишемо алгоритм розрахунку періодичного режиму в наведеній схемі. Припускаємо, що відомі: період коливань , кількість врахованих гармонік N, нелінійні функції  та їх похідні, значення лінійних провідностей схеми на постійному струмі та на частотах гармонік (тобто матриця Y), число точок М на періоді для виконання дискретного перетворення Фур’є.

Крок 1: ввести початкове значення вектора .

Крок 2: розрахувати за формулою (14) та за компонентами вектора  миттєві значення напруги  в М точках періоду .

Крок 3: розрахувати з вольт-амперної  та вольт-кулонівської  характеристик миттєві значення струму крізь нелінійний опір та заряд на нелінійній ємності в М точках періоду , а також розрахувати компоненти векторів  за допомогою дискретного перетворення Фур’є.

Крок 4: визначити вектор незв’язності  за допомогою (11), (12).

Крок 5: перевірити виконання нерівності ; якщо вона виконується, то закінчити; якщо ні, то перейти до кроку 6.

Крок 6: розрахувати миттєві значення  і  в М точках на періоді та знайти за допомогою дискретного перетворення Фур’є спектральний склад g(t) і c(t).

Крок 7: сформувати матрицю Якобі, користуючись (10), (11), (12).

Крок 8: вирішити систему лінійних рівнянь (12) відносно компонент вектора ; покласти  і повернутися до кроку 2.

Обміркуємо особливості розрахунку періодичного режиму автогенератора. Припустимо, в схемі (рис. 1) джерело струму  замінили джерелом живлення , який задає робочу точку на нелінійних елементах. Припустимо, що в вольт-амперній характеристиці нелінійного опору є спадаюча ділянка, в середині якої вибрана робоча точка. За цих умов у схемі можуть збудитись автоколивання, які описуються рівнянням, складеним для змінних напруги, струму і заряду відносно робочої точки

.

Якщо в це рівняння підставити (11), (12), (13) і зробити, як раніше, ряд перетворень, то можна отримати рівняння (8), в яких , , де  - невідомий період. Таким чином, кількість невідомих на одиницю більше, ніж кількість рівнянь. Щоб привести у відповідність кількість невідомих і рівнянь, вважаємо

.

З цього виразу випливає, що перша гармоніка напруги не має квадратурної (синусної) складової. Такий запис справедливий тому, що в автогенераторі фаза коливань випадкова. В результаті кількість спектральних складових напруги зменшилась на одиницю.

Щоб виразніше уявити специфіку розрахунку, підставимо в (8) N=1 і запишемо систему рівнянь автогенератора в дійсній формі

,

, (14)

.

Тут позначено  . Оскільки прийнято , то

Якщо маємо аналітичну залежністю  і  від частоти , то можна ввести вектор , записати рівняння (14) у вигляді  і вирішити їх методом Ньютона. При цьому для елементів матриці Якобі вдається утворити аналітичний вираз і алгоритм розрахунків збігається з попереднім.

Якщо програма не орієнтована на отримання аналітичного виразу для  і , то можна зробити таким чином. Подамо перші два рівняння до (14) у векторно-матричної формі

, (15)

а останнє перепишемо як

, (16)

де  - діагональна матриця;

, .

Вирішуватимемо (15) методом Ньютона при , а (16) послідовним зближенням або методом Стефенсена при . Обчислення повинні бути організовані так, щоб після вирішення одного рівняння його результати вводились в друге як початкові значення і навпаки. Розрахунки припиняються, якщо норма різності векторів  на сусідніх ітераціях стане менша, ніж задана похибка.