Модель сети типа радиально-базисной функции

4.4 Модель сети типа радиально-базисной функции

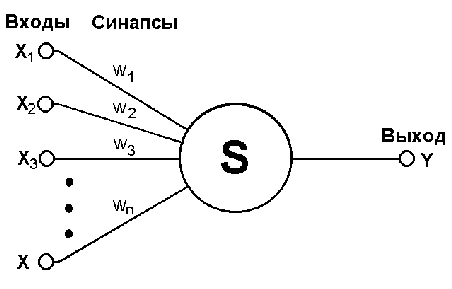
Радиально-базисные сети были предложены для аппроксимации функций многих переменных. C помощью радиально-базисных функций можно сколь угодно точно аппроксимировать заданную функцию. Как и многослойный персептрон, радиально-базисная сеть является универсальным аппроксиматором. Математическую основу РБ-сети составляет метод потенциальных функций, разработанный М.А. Айзерманом, Э.М. Браверианом и Л.И. Розоноэром, позволяющий представить некоторую функцию у(х) в виде суперпозиции потенциальных или базисных функций f_i(x)

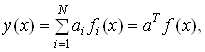(4.9)

где a_i(t) = (a₁, a₂,..., a_N)^T – вектор подлежащих определению параметров; f(x) = (f₁(x), f₂(x),..., f_N(x))^T – вектор базисных функций.

В РБС в качестве базисных выбираются некоторые функции расстояния между векторами

(4.10)

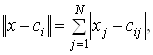Векторы с_i называют центрами базисных функций. Функции f_i(x) выбираются неотрицательными и возрастающими при увеличении . В качестве меры близости векторов х и c_i выбираются обычно либо евклидова метрика  либо манхэттенская  где

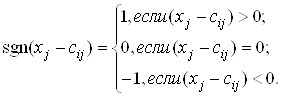(4.11)

Радиально-базисные сети обладают большой скоростью обучения. При их обучении не возникает проблем с «застреванием» в локальных минимумах. Однако в связи с тем, что при выполнении непосредственно классификации проводятся довольно сложные вычисления, возрастает время получения результата.

4.4.1 Структура РБФ

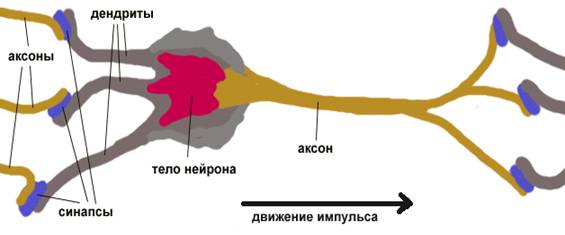
Структура РБФ соответствует сети прямого распространения первого порядка (рисунок 4.10).

Информация об образах передается с входного слоя на скрытый, являющийся шаблонным и содержащий ρ нейронов. Каждый нейрон шаблонного слоя, получая полную информацию о входных сигналах х, вычисляет функцию

(4.12)

где вектор входных сигналов ; c_i - вектор центров ; R – весовая матрица.

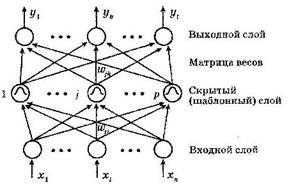
Рисунок 4.10 – Структура радиально-базисной сети

Особенностью данных сетей является наличие радиально-симметричного шаблонного слоя, в котором анализируется расстояние  между входным вектором и центром, представленным в виде вектора во входном пространстве. Вектор центров определяется по обучающей выборке и сохраняется в пространстве весов от входного слоя к слою шаблонов.

Рассмотрим нейрон шаблонного слоя сети. На рисунке 4.11 представлен i-й нейрон шаблонного слоя РБ-сети. Обработку поступающей на него информации условно можно разделить на два этапа: на первом вычисляется расстояние между предъявленным образом х и вектором центров с_i с учетом выбранной метрики и нормы матрицы R, на втором это расстояние преобразуется нелинейной активационной функцией f(x). Двойные стрелки на рисунке обозначают векторные сигналы, а тройные - матричный сигнал.

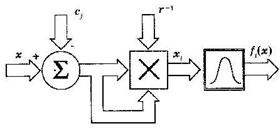
Рисунок 4.11 – Нейрон шаблонного слоя РБС

В качестве функции преобразования  наиболее часто выбираются следующие:

– гауссова функция

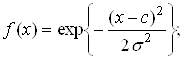(4.13)

– мультиквадратичная функция

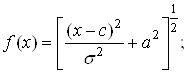(4.14)

– обратная мультиквадратичная функция

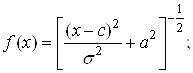(4.15)

– сплайн-функция

(4.16)

– функция Коши

(4.17)

Норма матрицы R^-1 определяет положение осей в пространстве. В общем виде матрица R^-1 может быть представлена следующим образом:

(4.18)

Весовую матрицу R₁ также называют обратной ковариационной матрицей. Элементы этой матрицы равны

 (4.19)

Здесь  – некоторые управляемые параметры.

Часто матрица R^-1 выбирается диагональной, т.е.  для i≠j, и более того, принимают

Величина сигнала j-го нейрона выходного слоя у_j зависит от того, насколько близок предъявляемый входной сигнал х запомненному этим нейроном центру с_j. Значение у_j определяется как взвешенная сумма функций (4.9), т.е.

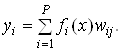(4.20)

Обычно выходными сигналами сети являются нормализованные значения  вычисленные по формуле

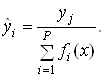(4.21)

4.4.2 Обучение РБФ

РБ-сеть характеризуют три типа параметров:

– линейные весовые параметры выходного слоя w_ijвходят в описание сети линейно);

– центры c_i – нелинейные (входят в описание нелинейно) параметры скрытого слоя;

– отклонения (радиусы базисных функций) σ_ij – нелинейные параметры скрытого слоя.

Обучение сети, состоящее в определении этих параметров, может сводиться к одному из следующих вариантов:

1. Задаются центры и отклонения, а вычисляются только веса выходного слоя.

2. Определяются путем самообучения центры и отклонения, а для коррекции весов выходного слоя используется обучение с учителем.

3. Определяются все параметры сети с помощью обучения с учителем.

Первые два варианта применяются в сетях, использующих базисные функции с жестко заданным радиусом (отклонением). Третий же вариант, являясь наиболее сложным и трудоемким в реализации, предполагает использование любых базисных функций.

Таким образом, обучение сети заключается в следующем:

– определяются центры c_i;

– выбираются параметры σ_i;

– вычисляются элементы матрицы весов W.

Рассмотрим методику выбора параметров центров и отклонений σ. Центры c_i определяют точки, через которые должна проходить аппроксимируемая функция. Поскольку большая обучающая выборка приводит к затягиванию процесса обучения, в РБ-сетях широко используется кластеризация образов, при которой схожие векторы объединяются в кластеры, представляемые затем в процессе обучения только одним вектором. В настоящее время существует достаточно большое число эффективных алгоритмов кластеризации.

Использование кластеризации отражается на формулах (4.20), (4.21) следующим образом:

(4.22)

где m_i - число входных векторов в i-м кластере.

В наиболее простом варианте алгоритм кластеризации, алгоритм k-среднего, направляет каждый образ в кластер, имеющий ближайший к данному образу центр. Если количество центров заранее задано или определено, алгоритм, обрабатывая на каждом такте входной вектор сети, формирует в пространстве входов сети центры кластеров. С ростом числа тактов эти центры сходятся к центрам данных. Кандидатами в центры являются все выходы скрытого слоя, однако в результате работы алгоритма будет сформировано подмножество наиболее существенных выходов.

Как уже указывалось, параметр σ_i, входящий в формулы для функций преобразования, определяет разброс относительно центра с_i. Варьируя параметры c_i и σ_i, пытаются перекрыть все пространство образов, не оставляя пустот. Используя метод k-ближайших соседей, определяют k соседей центра c_i и, усредняя, вычисляют среднее значение  Величина отклонения  от c_i служит основанием для выбора параметра σ_i. На практике часто оправдывает себя выбор

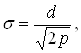(4.23)

где d=max(c_i – c_k) - максимальное расстояние между выбранными центрами; р - количество нейронов шаблонного слоя (образов).

Если качество аппроксимации является неудовлетворительным, выбор параметров c_i и σ, а также определение весов W повторяют до тех пор, пока полученное решение не окажется удовлетворительным.

Похожие работы

Искусственные нейронные сети

Скачать

60598

0

10

... . Если же задача не может быть сведена ни к одному из известных классов, разработчику приходится решать задачу синтеза новой конфигурации. Проблема синтеза искусственной нейронной сети сильно зависит от задачи, дать общие подробные рекомендации затруднительно. В большинстве случаев оптимальный вариант искусственной нейронной сети получается опытным путем. Искусственные нейронные сети могут быть ...

Функционирование рынка ценных бумаг в условиях нестабильной экономики России

Скачать

185716

7

6

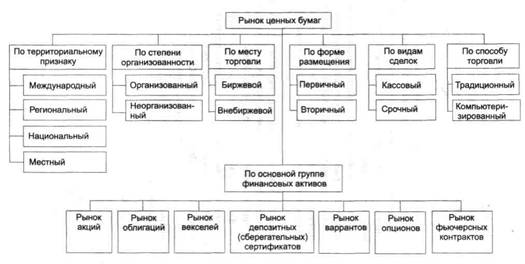
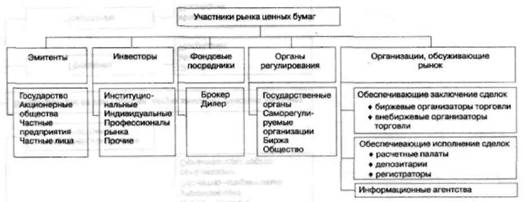
... важной составной частью как денежного рынка, так и рынка капиталов, которые в совокупности составляют финансовый рынок. Цель функционирования рынка ценных бумаг -как и всех финансовых рынков - состоит в том, чтобы обеспечивать наличие механизма для привлечения инвестиций в экономику путем установления необходимых контактов между теми, кто нуждается в средствах, и теми, кто хотел бы инвестировать ...

Информационные технологии при анализе бизнеса

Скачать

256482

15

25

... самой постановки задачи реализации анализа бизнеса в среде современных информационных технологий, становится тормозом в развитии не только информационных технологий при анализе бизнеса и их применения, но и оказывают негативное влияние на развитие самого анализа бизнеса как направления. Выводы 1. Исследование методической базы анализа стоимости бизнеса, проводимое на основе затратного, ...

Методы формирования нейросетей. Сущность электронного документооборота

Скачать

107679

0

1

... задач за счет применения средств автоматизации, снижение затрат за счет сокращения штата сотрудников, привлекаемых к делопроизводству, поиску и сортировке управленческой документации за счет внедрения электронного документооборота и т.д.) Результаты второго рода могут быть измерены с помощью экономических показателей, находящихся в бухгалтерской отчетности. Доход третьего рода получают за счет ...