Навигация
Построение математических моделей прогнозирования объема продаж
2.2 Построение математических моделей прогнозирования объема продаж
Безусловно, в условиях рыночной экономики, главным показателем рентабельности предприятия является прибыль. И здесь незаменимы методы математической статистики, которые позволяют правильно оценить, какие факторы, и в какой степени влияют на прибыль, а так же на основании правильно построенной математической модели, спрогнозировать прибыль на будущий период.
Проведем статистический анализ исходных данных, полученных при исследовании основных показателей деятельности предприятия, с целью выявления доминирующих факторов влияющих на прибыль и построения адекватной математической модели для изучения возможностей ее максимизации и прогнозирования на последующие периоды.
Исходные данные для поставленного задания приведены в таблице 4.
Таблица 4 Исходные данные для регрессионного анализа
|
| Прибыль | Коэффициент качества продукции | Доля в общем объеме продаж | Розничная цена | Коэффициент издержек на 1 продукции | Удовлетворение условий розничных торговцев |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| № | Y, % | X1 | X2 | X3 | X4 | X5 |
| 1 | 1,99 | 1,22 | 1,24 | 1,3 | 35,19 | 2,08 |
| 2 | 12,21 | 1,45 | 1,54 | 1,04 | 80 | 1,09 |
| 3 | 23,07 | 1,9 | 1,31 | 1 | 23,31 | 2,28 |
| 4 | 24,14 | 2,53 | 1,36 | 1,64 | 80 | 1,44 |
| 5 | 35,05 | 3,41 | 2,65 | 1,19 | 80 | 1,75 |
| 6 | 36,87 | 1,96 | 1,63 | 1,26 | 68,84 | 1,54 |
| 7 | 4,7 | 2,71 | 1,66 | 1,28 | 80 | 0,47 |
| 8 | 58,45 | 1,76 | 1,4 | 1,42 | 30,32 | 2,51 |
| 9 | 59,55 | 2,09 | 2,61 | 1,65 | 80 | 2,81 |
| 10 | 61,42 | 1,1 | 2,42 | 1,24 | 32,94 | 0,59 |
| 11 | 61,51 | 3,62 | 3,5 | 1,09 | 28,56 | 0,64 |
| 12 | 61,95 | 3,53 | 1,29 | 1,29 | 78,75 | 1,73 |
| 13 | 71,24 | 2,09 | 2,44 | 1,65 | 38,63 | 1,83 |
| 14 | 71,45 | 1,54 | 2,6 | 1,19 | 48,67 | 0,76 |
| 15 | 81,88 | 2,41 | 2,11 | 1,64 | 40,83 | 0,14 |
| 16 | 10,08 | 3,64 | 2,06 | 1,46 | 80 | 3,53 |
| 17 | 10,25 | 2,61 | 1,85 | 1,59 | 80 | 2,13 |
| 18 | 10,81 | 2,62 | 2,28 | 1,57 | 80 | 3,86 |
| 19 | 11,09 | 3,29 | 4,07 | 1,78 | 80 | 1,28 |
| 20 | 12,64 | 1,24 | 1,84 | 1,38 | 31,2 | 4,25 |
| 21 | 12,92 | 1,37 | 1,9 | 1,55 | 29,49 | 3,98 |
Основная цель первой части задания оценить влияние на прибыль предприятия от реализации продукции одного вида следующих факторов:
- Х1 - коэффициент качества продукции;
- Х2 - доля в общем объеме продаж;
- Х3 – розничная цена продукции;
- Х4 – коэффициент издержек на единицу продукции;
- Х5 – удовлетворение условий розничных торговцев.
Необходимо, применив регрессионные методы анализа, построить математическую модель зависимости прибыли от некоторых (или всех) из вышеперечисленных факторов и проверить адекватность полученной модели.
Прежде чем применить данным метод регрессионного анализа, необходимо провести некоторый предварительный анализ имеющихся в распоряжении выборок. Это позволит сделать выводы о качестве имеющихся данных, а именно: о наличии или отсутствии тренда, нормальном законе распределения выборки, оценить некоторые статистические характеристики и так далее.
Для всех последующих расчетов примем уровень значимости 0,05, что соответствует 5% вероятности ошибки.
Исследование выборки по прибыли (Y).
- Математическое ожидание (арифметическое среднее) 34,91761905.
- Доверительный интервал для математического ожидания (22,75083;47,08441).
- Дисперсия (рассеивание) 714,402159.
- Доверительный интервал для дисперсии (439,0531; 1564,384).
- Средне квадратичное отклонение (от среднего) 26,72830258.
- Медиана выборки 24,14.
- Размах выборки 79,89.
- Асимметрия (смещение от нормального распределения) 0,370221636.
- Эксцесс выборки (отклонение от нормального распределения) -1,551701276.
- Коэффициент вариации (коэффициент представительности среднего) 77%.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия серий. Результаты проверки представлены в таблице 5 (2-й столбец). Сумма серий равняется 5. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 5 до 15, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия инверсий. Количество инверсий представлено в таблице 5 (3-й столбец). Сумма инверсий равняется 81. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 64 до 125, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Таблица 5 Критерии серий и инверсий
| Прибыль Y % | Критерий серий | Критерий инверсий |
| 1 | 2 | 3 |
| 1,99 | - | 0 |
| 12,21 | - | 5 |
| 23,07 | - | 7 |
| 24,14 | + | 7 |
| 35,05 | + | 7 |
| 36,87 | + | 7 |
| 4,7 | - | 0 |
| 58,45 | + | 6 |
| 59,55 | + | 6 |
| 61,42 | + | 6 |
| 61,51 | + | 6 |
| 61,95 | + | 6 |
| 71,24 | + | 6 |
| 71,45 | + | 6 |
| 81,88 | + | 6 |
| 10,08 | - | 0 |
| 10,25 | - | 0 |
| 10,81 | - | 0 |
| 11,09 | - | 0 |
| 12,64 | - | 0 |
| 12,92 | - | 0 |
| Итого | 5 | 81 |
Проверка гипотезы о нормальном законе распределения выборки с применением критерия ![]() . Разобьем выборку на интервалы группировки длиной 0,4*среднеквадратичное отклонение = 10,69132103. Получим следующее количество интервалов группировки размах/длина интервала=7.Все данные о границах интервалов, теоретических и эмпирических частотах приведены в таблице 6
. Разобьем выборку на интервалы группировки длиной 0,4*среднеквадратичное отклонение = 10,69132103. Получим следующее количество интервалов группировки размах/длина интервала=7.Все данные о границах интервалов, теоретических и эмпирических частотах приведены в таблице 6
Таблица 6 Критерий ![]()
| Интервалы группировки | Теоретическая частота | Расчетная частота |
| 1 | 2 | 3 |
| 12,68132103 | 0,221751084 | 4 |
| 23,37264207 | 0,285525351 | 2 |
| 34,0639631 | 0,313282748 | 1 |
| 44,75528414 | 0,2929147 | 2 |
| 55,44660517 | 0,233377369 | 0 |
| 66,1379262 | 0,158448887 | 5 |
| 76,82924724 | 0,091671119 | 2 |
Результирующее значение критерия 2,11526E-55 значительно меньше табличного 12,6 – следовательно, гипотеза о нормальности закона распределения принимается с уровнем значимости 0,05.
Исследование выборки по коэффициенту качества продукции (Х1).
- Математическое ожидание (арифметическое среднее) 2,29.
- Доверительный интервал для математического ожидания (1,905859236; 2,674140764).
- Дисперсия (рассеивание) 0,71215.
- Доверительный интервал для дисперсии (0,437669008; 1,559452555).
- Средне квадратичное отклонение (от среднего) 0,843889803.
- Медиана выборки 2,09.
- Размах выборки 2,54.
- Асимметрия (смещение от нормального распределения) 0,290734565.
- Эксцесс выборки (отклонение от нормального распределения) -1,161500717.
- Коэффициент вариации (коэффициент представительности среднего) 37%.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия серий. Результаты проверки представлены в таблице 7 (2-й столбец). Сумма серий равняется 11. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 5 до 15, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается. Проверка статистической независимости выборки (проверка наличия тренда) методом критерия инверсий. Количество инверсий представлено в таблице 7 (3-й столбец). Сумма инверсий равняется 89. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 64 до 125, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Таблица 7 Критерии серий и инверсий
| Коэффициент качества продукции Х1 | Критерий серий | Критерий инверсий |
| 1 | 2 | 3 |
| 1,22 | - | 1 |
| 1,45 | - | 3 |
| 1,9 | - | 5 |
| 2,53 | + | 9 |
| 3,41 | + | 13 |
| 1,96 | - | 5 |
| 2,71 | + | 10 |
| 1,76 | - | 4 |
| 2,09 | + | 4 |
| 1,1 | - | 0 |
| 3,62 | + | 9 |
| 3,53 | + | 8 |
| 2,09 | + | 3 |
| 1,54 | - | 2 |
| 2,41 | + | 2 |
| 3,64 | + | 5 |
| 2,61 | + | 2 |
| 2,62 | + | 2 |
| 3,29 | + | 2 |
| 1,24 | - | 0 |
| 1,37 | - | 0 |
| Итого | 11 | 89 |
Проверка гипотезы о нормальном законе распределения выборки с применением критерия ![]() . Разобьем выборку на интервалы группировки длиной 0,4*среднеквадратичное отклонение = 0,337555921. Получим следующее количество интервалов группировки размах/длина интервала=7. Все данные о границах интервалов, теоретических и эмпирических частотах приведены в таблице 8
. Разобьем выборку на интервалы группировки длиной 0,4*среднеквадратичное отклонение = 0,337555921. Получим следующее количество интервалов группировки размах/длина интервала=7. Все данные о границах интервалов, теоретических и эмпирических частотах приведены в таблице 8
Таблица 8 Критерий ![]()
| Интервалы группировки | Теоретическая частота | Расчетная частота |
| 1 | 2 | 3 |
| 1,437555921 | 5,960349765 | 4 |
| 1,775111843 | 8,241512255 | 3 |
| 2,112667764 | 9,71079877 | 4 |
| 2,450223685 | 9,750252967 | 1 |
| 2,787779606 | 8,342374753 | 4 |
| 3,125335528 | 6,082419779 | 0 |
| 3,462891449 | 3,778991954 | 2 |
Результирующее значение критерия 0,000980756 значительно меньше табличного 12,6 – следовательно, гипотеза о нормальности закона распределения принимается с уровнем значимости 0,05.
Исследование выборки по доле в общем объеме продаж (Х2).
- Математическое ожидание (арифметическое среднее) 2,083809524.
- Доверительный интервал для математического ожидания (1,748443949; 2,419175098).
- Дисперсия (рассеивание) 0,542784762.
- Доверительный интервал для дисперсии (0,333581504; 1,188579771).
- Средне квадратичное отклонение (от среднего) 0,736739277.
- Медиана выборки 1,9.
- Размах выборки 2,83.
- Асимметрия (смещение от нормального распределения) 1,189037981.
- Эксцесс выборки (отклонение от нормального распределения) 1,48713312.
- Коэффициент вариации (коэффициент представительности среднего) 35%.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия серий. Результаты проверки представлены в таблице 9 (2-й столбец). Сумма серий равняется 11. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 5 до 15, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия инверсий. Количество инверсий представлено в таблице 9 (3-й столбец). Сумма инверсий равняется 89. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 64 до 125, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Таблица 9 Критерии серий и инверсий
| Коэффициент качества продукции Х2 | Критерий серий | Критерий инверсий |
| 1 | 2 | 3 |
| 1,24 | - | 0 |
| 1,54 | - | 4 |
| 1,31 | - | 1 |
| 1,36 | - | 1 |
| 2,65 | + | 14 |
| 1,63 | - | 2 |
| 1,66 | - | 2 |
| 1,4 | - | 1 |
| 2,61 | + | 10 |
| 2,42 | + | 7 |
| 3,5 | + | 9 |
| 1,29 | - | 9 |
| 2,44 | + | 6 |
| 1 | 2 | 3 |
| 2,6 | + | 6 |
| 2,11 | + | 4 |
| 2,06 | + | 3 |
| 1,85 | - | 1 |
| 2,28 | + | 2 |
| 4,07 | + | 2 |
| 1,84 | - | 0 |
| 1,9 | + | 0 |
| Итого | 10 | 84 |
Проверка гипотезы о нормальном законе распределения выборки с применением критерия ![]() . Разобьем выборку на интервалы группировки длиной 0,4*среднеквадратичное отклонение = 0,294695711. Получим следующее количество интервалов группировки размах/длина интервала=9. Все данные о границах интервалов, теоретических и эмпирических частотах приведены в таблице 10
. Разобьем выборку на интервалы группировки длиной 0,4*среднеквадратичное отклонение = 0,294695711. Получим следующее количество интервалов группировки размах/длина интервала=9. Все данные о границах интервалов, теоретических и эмпирических частотах приведены в таблице 10
Таблица 10 Критерий ![]()
| Интервалы группировки | Теоретическая частота | Расчетная частота |
| 1 | 2 | 3 |
| 1,534695711 | 8,613638207 | 5 |
| 1,829391421 | 10,71322271 | 3 |
| 2,124087132 | 11,35446101 | 5 |
| 2,418782843 | 10,25476697 | 1 |
| 2,713478553 | 7,892197623 | 5 |
| 3,008174264 | 5,175865594 | 0 |
| 3,302869975 | 2,892550245 | 0 |
| 3,597565686 | 1,377500344 | 1 |
| 3,892261396 | 0,559004628 | 1 |
Результирующее значение критерия 0,000201468 значительно меньше табличного 12,6 – следовательно, гипотеза о нормальности закона распределения принимается с уровнем значимости 0,05.
Исследование выборки по розничной цене (Х3).
- Математическое ожидание (арифметическое среднее) 1,390952381.
- Доверительный интервал для математического ожидания (1,287631388; 1,- 94273374).
- Дисперсия (рассеивание) 0,051519048.
- Доверительный интервал для дисперсии (0,031662277; 0,112815433).
- Средне квадратичное отклонение (от среднего) 0,226978077.
- Медиана выборки 1,38.
- Размах выборки 0,78.
- Асимметрия (смещение от нормального распределения) -0,060264426.
- Эксцесс выборки (отклонение от нормального распределения) -1,116579819.
- Коэффициент вариации (коэффициент представительности среднего) 16%.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия серий. Результаты проверки представлены в таблице 11(2-й столбец). Сумма серий равняется 8. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 5 до 15, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия инверсий. Количество инверсий представлено в таблице 11 (3-й столбец). Сумма инверсий равняется 68. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 64 до 125, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Таблица 11 Критерии серий и инверсий
| Розничная цена Х4 | Критерий серий | Критерий инверсий |
| 1 | 2 | 3 |
| 1,3 | - | 9 |
| 1,04 | - | 1 |
| 1 | - | 0 |
| 1,64 | + | 13 |
| 1,19 | - | 1 |
| 1,26 | - | 3 |
| 1,28 | - | 3 |
| 1,42 | + | 5 |
| 1,65 | + | 10 |
| 1,24 | - | 2 |
| 1,09 | - | 0 |
| 1,29 | - | 1 |
| 1,65 | + | 7 |
| 1,19 | - | 0 |
| 1,64 | + | 5 |
| 1,46 | + | 1 |
| 1,59 | + | 3 |
| 1,57 | + | 2 |
| 1,78 | + | 2 |
| 1,38 | + | 0 |
| 1,55 | + | 0 |
| Итого | 8 | 68 |
Проверка гипотезы о нормальном законе распределения выборки с применением критерия ![]() . Разобьем выборку на интервалы группировки длиной 0,4*среднеквадратичное отклонение = 0,090791231. Получим следующее количество интервалов группировки размах/длина интервала=8. Все данные о границах интервалов, теоретических и эмпирических частотах приведены в таблице 12
. Разобьем выборку на интервалы группировки длиной 0,4*среднеквадратичное отклонение = 0,090791231. Получим следующее количество интервалов группировки размах/длина интервала=8. Все данные о границах интервалов, теоретических и эмпирических частотах приведены в таблице 12
Таблица 12 Критерий ![]()
| Интервалы группировки | Теоретическая частота | Расчетная частота |
| 1 | 2 | 3 |
| 1,090791231 | 15,39563075 | 3 |
| 1,181582462 | 24,12028441 | 0 |
| 1,272373693 | 32,20180718 | 4 |
| 1,363164924 | 36,63455739 | 3 |
| 1,453956155 | 35,51522214 | 2 |
| 1,544747386 | 29,33938492 | 1 |
| 1,635538617 | 20,65381855 | 3 |
| 1,726329848 | 12,38975141 | 4 |
Результирующее значение критерия 3,27644E-33 значительно меньше табличного 12,6 – следовательно, гипотеза о нормальности закона распределения принимается с уровнем значимости 0,05.
Исследование выборки по коэффициенту издержек на единицу продукции (Х4).
- Математическое ожидание (арифметическое среднее) 57,46333333.
- Доверительный интервал для математического ожидания (46,70536237; 68- 22130429).
- Дисперсия (рассеивание) 558,5363233.
- Доверительный интервал для дисперсии (343,2620073; 1223,072241).
- Средне квадратичное отклонение (от среднего) 23,63337308.
- Медиана выборки 68,84.
- Размах выборки 56,69.
- Асимметрия (смещение от нормального распределения) --0,199328538.
- Эксцесс выборки (отклонение от нормального распределения) -1,982514776.
- Коэффициент вариации (коэффициент представительности среднего) 41%.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия серий. Результаты проверки представлены в таблице 13 (2-й столбец). Сумма серий равняется 11. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 5 до 15, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия инверсий. Количество инверсий представлено в таблице 13 (3-й столбец). Сумма инверсий равняется 89. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 64 до 125, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Таблица 13 Критерии серий и инверсий
| Розничная цена Х4 | Критерий серий | Критерий инверсий |
| 1 | 2 | 3 |
| 35,19 | - | 6 |
| 80 | + | 11 |
| 23,31 | - | 0 |
| 80 | + | 10 |
| 80 | + | 10 |
| 68,84 | + | 8 |
| 80 | + | 9 |
| 30,32 | - | 3 |
| 80 | + | 8 |
| 32,94 | - | 3 |
| 28,56 | - | 0 |
| 78,75 | + | 5 |
| 38,63 | - | 2 |
| 48,67 | - | 3 |
| 40,83 | - | 2 |
| 80 | + | 2 |
| 80 | + | 2 |
| 80 | + | 2 |
| 80 | + | 2 |
| 31,2 | - | 1 |
| 29,49 | - | 0 |
| Итого | 11 | 89 |
Проверка гипотезы о нормальном законе распределения выборки с применением критерия ![]() . Разобьем выборку на интервалы группировки длиной 0,4*среднеквадратичное отклонение = 9,453349234. Получим следующее количество интервалов группировки размах/длина интервала=5.Все данные о границах интервалов, теоретических и эмпирических частотах приведены в таблице 14
. Разобьем выборку на интервалы группировки длиной 0,4*среднеквадратичное отклонение = 9,453349234. Получим следующее количество интервалов группировки размах/длина интервала=5.Все данные о границах интервалов, теоретических и эмпирических частотах приведены в таблице 14
Таблица 14 Критерий ![]()
| Интервалы группировки | Теоретическая частота | Расчетная частота |
| 1 | 2 | 3 |
| 32,76334923 | 0,205311711 | 5 |
| 42,21669847 | 0,287891016 | 4 |
| 51,6700477 | 0,343997578 | 1 |
| 61,12339693 | 0,350264029 | 0 |
| 70,57674617 | 0,30391251 | 1 |
Результирующее значение критерия 3,27644E-33 значительно меньше табличного 12,6 – следовательно, гипотеза о нормальности закона распределения принимается с уровнем значимости 0,05.
Исследование выборки по коэффициенту удовлетворения условий розничных торговцев (Х5).
- Математическое ожидание (арифметическое среднее) 1,937619048.
- Доверительный интервал для математического ожидания (1,390131506; 2,485106589).
- Дисперсия (рассеивание) 1,446569048.
- Доверительный интервал для дисперсии (0,889023998; 3,167669447).
- Средне квадратичное отклонение (от среднего) 1,202733989.
- Медиана выборки 1,75.
- Размах выборки 4,11.
- Асимметрия (смещение от нормального распределения) --0,527141402.
- Эксцесс выборки (отклонение от нормального распределения) -0,580795634.
- Коэффициент вариации (коэффициент представительности среднего) 62%.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия серий. Результаты проверки представлены в таблице 15 (2-й столбец). Сумма серий равняется 13. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 5 до 15, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Проверка статистической независимости выборки (проверка наличия тренда) методом критерия инверсий. Количество инверсий представлено в таблице 15 (3-й столбец). Сумма инверсий равняется 80. Поскольку данное значение попадает в доверительный интервал (табличные значения) от 64 до 125, следовательно, гипотеза о статистической независимости и отсутствии тренда подтверждается.
Таблица 15 Критерии серий и инверсий
| Розничная цена Х4 | Критерий серий | Критерий инверсий |
| 1 | 2 | 3 |
| 2,08 | + | 12 |
| 1,09 | - | 5 |
| 2,28 | + | 12 |
| 1,44 | - | 6 |
| 1,75 | + | 8 |
| 1,54 | - | 6 |
| 0,47 | - | 1 |
| 2,51 | + | 8 |
| 2,81 | + | 8 |
| 0,59 | - | 1 |
| 0,64 | - | 1 |
| 1,73 | - | 3 |
| 1,83 | + | 3 |
| 0,76 | - | 1 |
| 0,14 | - | 0 |
| 3,53 | + | 2 |
| 2,13 | + | 1 |
| 3,86 | + | 1 |
| 1,28 | - | 0 |
| 4,25 | + | 1 |
| 3,98 | + | 0 |
| Итого | 13 | 80 |
Проверка гипотезы о нормальном законе распределения выборки с применением критерия ![]() . Разобьем выборку на интервалы группировки длиной 0,4*среднеквадратичное отклонение = 0,481093595. Получим следующее количество интервалов группировки размах/длина интервала=8.Все данные о границах интервалов, теоретических и эмпирических частотах приведены в таблице 16
. Разобьем выборку на интервалы группировки длиной 0,4*среднеквадратичное отклонение = 0,481093595. Получим следующее количество интервалов группировки размах/длина интервала=8.Все данные о границах интервалов, теоретических и эмпирических частотах приведены в таблице 16
Таблица 16 Критерий ![]()
| Интервалы группировки | Теоретическая частота | Расчетная частота |
| 1 | 2 | 3 |
| 0,621093595 | 3,826307965 | 3 |
| 1,102187191 | 5,47254967 | 3 |
| 1,583280786 | 6,669793454 | 3 |
| 2,064374382 | 6,927043919 | 3 |
| 2,545467977 | 6,130506823 | 4 |
| 3,026561573 | 4,623359901 | 1 |
| 3,507655168 | 2,971200139 | 0 |
| 3,988748764 | 1,627117793 | 3 |
Результирующее значение критерия 0,066231679 значительно меньше табличного 12,6 – следовательно, гипотеза о нормальности закона распределения принимается с уровнем значимости 0,05.
Для оценки степени зависимости между переменными модели построим корреляционную матрицу, и для каждого коэффициента корреляции в матрице рассчитаем V-функцию, которая служит для проверки гипотезы об отсутствии корреляции между переменными.
Таблица 17 Корреляционная матрица
| Y | X1 | X2 | X3 | X4 | X5 | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Y | R | 0,95238 | 0,00950 | 0,21252 | -0,01090 | -0,30012 | -0,42102 |
| V | 8,30380 | 0,04247 | 0,96511 | -0,04873 | -1,38479 | -2,00769 | |
| X1 | R | 0,00950 | 0,95238 | 0,36487 | 0,13969 | 0,50352 | -0,12555 |
| V | 0,04247 | 8,30380 | 1,71054 | 0,62883 | 2,47761 | -0,56445 | |
| X2 | R | 0,21252 | 0,36487 | 0,95238 | 0,23645 | 0,06095 | -0,19187 |
| V | 0,96511 | 1,71054 | 8,30380 | 1,07781 | 0,27291 | -0,86885 | |
| X3 | R | -0,01090 | 0,13969 | 0,23645 | 0,95238 | 0,24228 | 0,25014 |
| V | -0,04873 | 0,62883 | 1,07781 | 8,30380 | 1,10549 | 1,14293 | |
| X4 | R | -0,30012 | 0,50352 | 0,06095 | 0,24228 | 0,95238 | -0,03955 |
| V | -1,38479 | 2,47761 | 0,27291 | 1,10549 | 8,30380 | -0,17694 | |
| X5 | R | -0,42102 | -0,12555 | -0,19187 | 0,25014 | -0,03955 | 0,95238 |
| V | -2,00769 | -0,56445 | -0,86885 | 1,14293 | -0,17694 | 8,30380 |
Гипотеза о нулевой корреляции принимается при –1,96<V<1,96, значения, для которых это условие не выполняется, выделены жирным шрифтом цветом. Следовательно, значимая зависимость имеет место между Y и Х5, а также Х1 и Х4.
Для построения математической модели выдвинем гипотезу о наличии линейной зависимости между прибылью (иначе Y) и факторами на нее влияющими (Х1, Х2, Х3, Х4, Х5). Следовательно, математическая модель может быть описана уравнением вида:
![]() ,(2.2.1)
,(2.2.1)
где ![]() - линейно-независимые постоянные коэффициенты.
- линейно-независимые постоянные коэффициенты.
Для их отыскания применим множественный регрессионный анализ. Результаты регрессии сведены в таблицы 18-20
Таблица 18 Регрессионная статистика
| 1 | 2 |
| Множественный R | 0,609479083 |
| R-квадрат | 0,371464753 |
| Нормированный R-квадрат | 0,161953004 |
| Стандартная ошибка | 24,46839969 |
| Наблюдения | 21 |
Таблица 19 Дисперсионная таблица
| Степени свободы | SS | MS | F | Значимость F | |
| 1 | 2 | 3 | 4 | 5 | 6 |
| Регрессия | 5 | 5307,504428 | 1061,500886 | 1,773002013 | 0,179049934 |
| Остаток | 15 | 8980,538753 | 598,7025835 | ||
| Итого | 20 | 14288,04318 |
Таблица 20 Коэффициенты регрессии
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| B0 | 38,950215 | 35,7610264 | 1,0891805 | 0,29326 | -37,272 | 115,173 | -37,2726 | 115,173 |
| B1 | 4,5371110 | 8,42440677 | 0,5385674 | 0,59808 | -13,419 | 22,4933 | -13,4190 | 22,4933 |
| B2 | 1,8305781 | 8,73999438 | 0,2094484 | 0,83691 | -16,798 | 20,4594 | -16,7982 | 20,4594 |
| B3 | 23,645979 | 27,4788285 | 0,8605162 | 0,40304 | -34,923 | 82,2157 | -34,9237 | 82,2157 |
| B4 | -0,526248 | 0,28793074 | -1,827690 | 0,08755 | -1,1399 | 0,08746 | -1,13995 | 0,08746 |
| B5 | -10,780037 | 4,95649626 | -2,174931 | 0,04604 | -21,344 | -0,21550 | -21,3445 | -0,21550 |
Таким образом, уравнение, описывающее математическую модель, приобретает вид:
Y=4,53711108952303*X1+1,830578196*X2+23,64597929*X3- 0,526248308*X5-10,78003746*X5+38,95021506. (2.2.2)
Для оценки влияния каждого из факторов на результирующую математическую модель применим метод множественной линейной регрессии к нормированным значениям переменных ![]() , результаты пересчета коэффициентов приведены в таблице 21
, результаты пересчета коэффициентов приведены в таблице 21
Таблица 21 Оценка влияния факторов
| Коэффициенты | Стандартная ошибка | t-статистика | |
| 1 | 2 | 3 | 4 |
| Y-пересечение | 38,95021506 | 35,76102644 | 1,089180567 |
| Переменная X 1 | 3,828821785 | 7,109270974 | 0,538567428 |
| Переменная X 2 | 1,348658856 | 6,439097143 | 0,209448441 |
| Переменная X 3 | 5,367118917 | 6,237091662 | 0,86051628 |
| Переменная X 4 | -12,43702261 | 6,804774783 | -1,827690556 |
| Переменная X 5 | -12,96551745 | 5,961346518 | -2,174931018 |
Коэффициенты в таблице 21 показывают степень влияния каждой из переменных на результат (Y). Чем больше коэффициент, тем сильнее прямая зависимость (отрицательные коэффициенты показывают обратную зависимость).
F-критерий из таблицы 19 показывает степень адекватности полученной математической модели.
Похожие работы
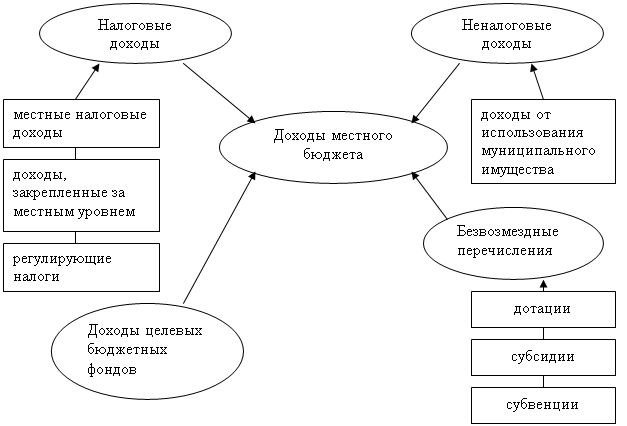
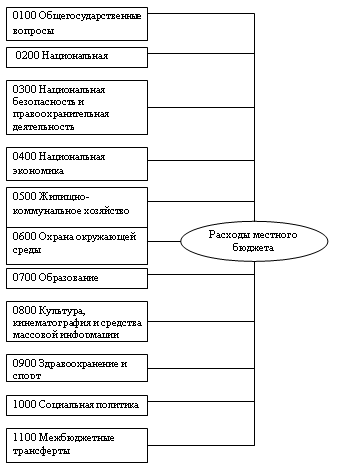
... проведения повседневной и целенаправленной работы по организации и управлению бюджетным процессом. Предметом исследования являются процессы управления доходами и расходами бюджета муниципального образования. - сбор необходимого материала для проведения научных изысканий; - получение опыта самостоятельной научно-исследовательской работы. Финансовая политика органов местного самоуправления имеет ...
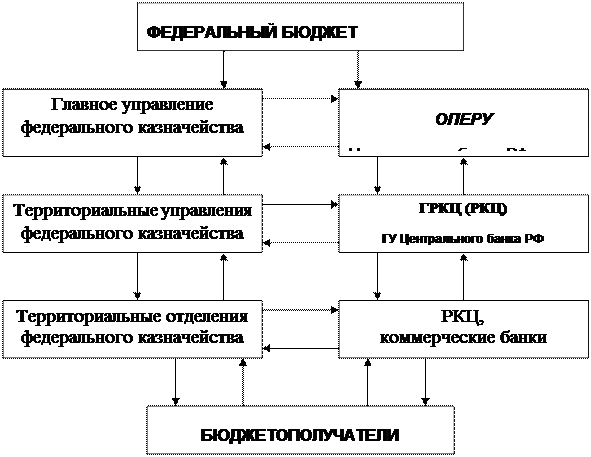
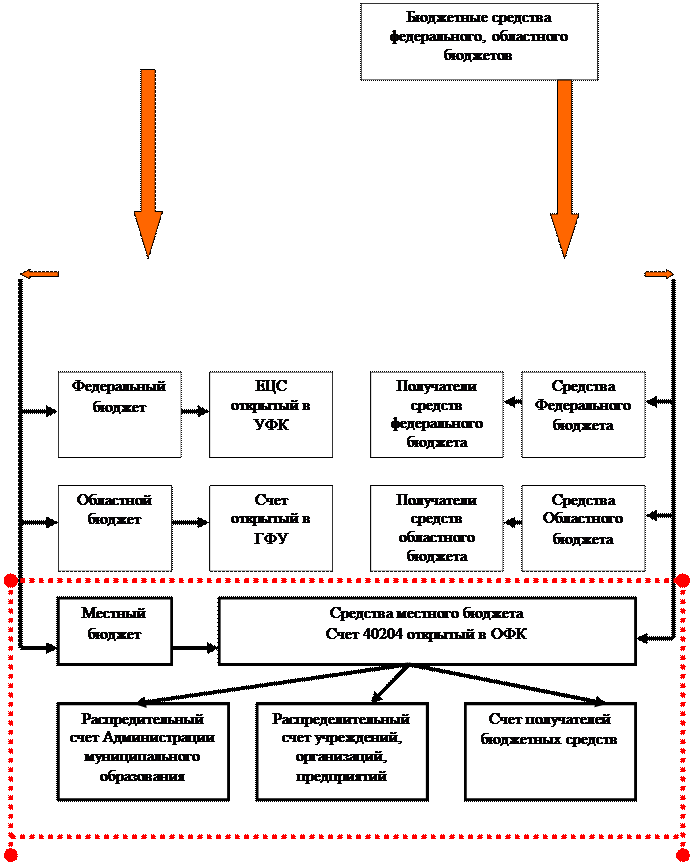
... в объеме имеющихся полномочий применительно к средствам федерального бюджета. 2. Общие сведения об объекте исследования деятельности Федерального Казначейства. 2.1. Характеристика объекта исследования В любой стране бюджет-это наиболее точная форма выражения существа государственной власти, а процесс его исполнения наглядно демонстрирует ее настоящий ...
... ) нормативов осуществляется по завершении данного бюджетного периода в процессе разработки бюджета на новый бюджетный период. 1.4 Влияние режимов налогообложения на уровень доходов индивидуальных предпринимателей Организация и ведение бухгалтерского и налогового учета зависит от того, какую систему налогообложения выберет налогоплательщик – индивидуальный предприниматель. Требования к ...
... помощи уволенным работникам в трудоустройстве, проведение информационно-разъяснительной работы. Глава 3. Усиление роли социальных аспектов в управлении персоналом в ООО «ТверьИнформПродукт» 3.1 Рекомендации по совершенствованию системы адаптации и профориентации сотрудников организации Основанием для совершенствования системы адаптации служит тот факт, что эффективной системы ...


0 комментариев