Метод Крылова

1.2 Метод Крылова

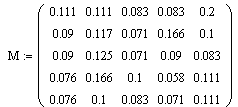
Метод Крылова основан на свойстве квадратной матрицы М обращать в нуль свой характеристический многочлен. В данной работе матрица М -это матрица коэффициентов технологических связей, которая имеет вид:

Согласно теореме Гамильтона-Кали, всякая квадратная матрица является корнем своего характеристического многочлена и, следовательно, обращает его в нуль. Пусть (1.2.1) характеристический многочлен

(1.2.1)

Заменяя в выражении величину λ на M, получаем

(1.2.2)

Взяв произвольный ненулевой вектор У⁰ и умножив обе части выражения (1.2.2) на него, получим:

(1.2.3)

Положим

  (1.2.4)

Тогда

(1.2.5)

Или в виде

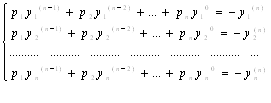
Если эта система имеет единственное решение, то ее корни р₁, р₂…..р_n, являются коэффициентами характеристического многочлена (1.2.1).

Если известны коэффициенты р₁, р₂…..р_n, и корни λ₁ , λ₂ ,….λ_nхарактеристического многочлена, то метод Крылова дает возможность найти соответствующие векторы по следующей формуле:

 , (1.2.6)

Здесь y^(n-1), y^(n-2), …. y⁽⁰⁾ – векторы, использованные при нахождении коэффициентов р₁, р₂…..р_nметодом Крылова, а коэффициенты q_ij() определяются по схеме Горнера

q_0i = 1, q_ij = λ_iq_i-1,i+p_i (1.2.7)

Для определения собственных чисел матрицы М необходимо решить полученное характеристическое уравнение. Для матрицы М это уравнение будет пятой степени, решать такое уравнение в данной работе будем решать, используя метод касательных или иначе метод Ньютона.

1.3 Метод Ньютона (метод касательных)

Метод Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Улучшением метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства.

Чтобы численно решить уравнение f (х) = 0 методом простой итерации, его необходимо привести к следующей форме: х = f(х), где f (х) -сжимающее отображение.

Для наилучшей сходимости метода в точке очередного приближения  должно выполняться условие . Решение данного уравнения ищут в виде , тогда:

(1.3.1)

В предположении, что точка приближения «достаточно близка» к корню , и что заданная функция непрерывна , окончательная формула для такова:

(1.3.2)

С учётом этого функция  определяется выражением

(1.3.3)

Эта функция в окрестности корня осуществляет сжимающее отображение, и алгоритм нахождения численного решения уравнения  сводится к итерационной процедуре вычисления:

(1.3.4)

По теореме Банаха последовательность приближений стремится к корню уравнения .

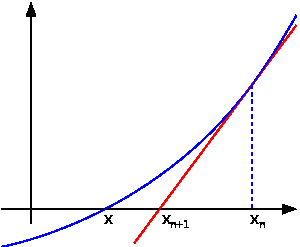
Рисунок 1.1- Графическое представление метода Ньютона

Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.

Достоинства метода Ньютона:

1) если минимизируемая функция является квадратической, то метод позволит найти минимум за один шаг;

2) если минимизируемая функция относится к классу поверхностей вращения, то метод также обеспечивает сходимость за один шаг;

3) если функция несимметрична, то метод не обеспечивает сходимость за конечное число шагов. Но для многих функций достигается гораздо более высокая скорость сходимости, чем при использовании других модификаций метода наискорейшего спуска.

Использование метода Крылова и метода Ньютона приведены в приложениях. Реализация методов производилась в среде МаthСАD и VB.Net.