Навигация
Реферат
На тему:
«Алгоритм Брезенхема»
Львів-2011
1. Алгоритм Брезенхема
Хоча алгоритм Брезенхема був спочатку розроблений для цифрових графопобудовувачів, однак він в тій же мірі підходить для використання растровими пристроями з ЕПТ. Алгоритм вибирає оптимальні растрові координати для представлення відрізка. У процесі роботи одна з координат – або x, або y (в залежності від кутового коефіцієнта) – змінюється на одиницю. Зміна іншої координати (на 0 чи 1) залежно від відстані між дійсним положенням відрізка і найближчих координат сітки. Таку відстань ми назвемо похибкою.
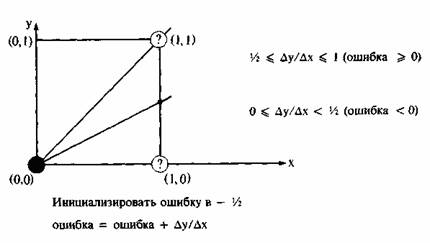
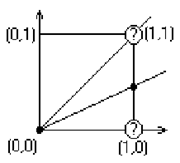
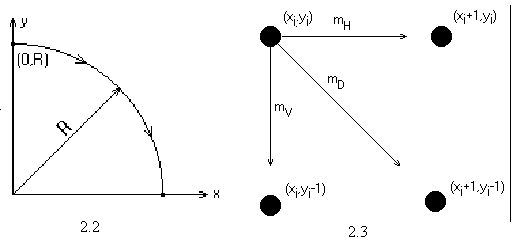
Алгоритм побудований так, що потрібно перевірити лише знак цієї похибки. На рис. 3.1 це ілюструється для відрізка в першому октанті, тобто для відрізка з кутовим коефіцієнтом, що лежить у діапазоні від 0 до 1. З малюнка можна помітити що, якщо кутовий коефіцієнт відрізка з точки (0,0) більший, ніж 1/2, то перетин з прямою x=1 буде розташований ближче до прямої y=1, ніж до прямої y=0. Отже, точка растра (1,1) краще апроксимує хід відрізка, ніж точка (1,0). Якщо кутовий коефіцієнт менше 1/2, то навпаки. для кутового коефіцієнта, рівного 1/2, немає кращого вибору. У даному випадку алгоритм вибирає точку (1,1).
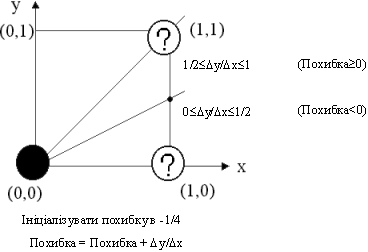
Основна ідея алгоритму Брезенхема
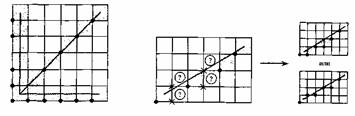
Не усі відрізки проходять через точки растра. Подібна ситуація ілюструється рис. 3.2, де відрізок з тангенсом кута нахилу 3/8 спочатку проходить через точку растра (0,0) і послідовно перетинає три піксели. Також ілюструється обчислення похибки при представленні відрізка дискретними пікселами.
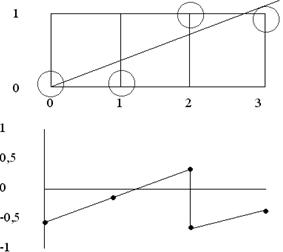
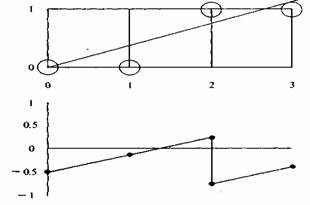
Графік похибки в алгоритмі Брезенхема
Тому що бажано перевіряти тільки знак похибки, то вона спочатку встановлюється рівною -1/2. Таким чином, якщо кутовий коефіцієнт відрізка дорівнює чи більший 1/2, то величина похибки в наступній точці растра з координатами (1,0) може бути обчислена як
e=e+m
де m – кутовий коефіцієнт. У нашому випадку при початковому значенні похибки -1/2
e=-1/2+3/8=-1/8
Тому що е від’ємне, відрізок пройде нижче середини піксела. Отже, піксел на тому ж самому горизонтальному рівні краще апроксимує положення відрізка, тому в не збільшується. Аналогічно обчислюємо похибку e=-1/8+3/8=1/4 у наступній точці растра (2,0). Тепер е додатне, значить відрізок пройде вище середньої точки. Растровий елемент (2,1) з наступною по величині координатою в краще апроксимує положення відрізка. Отже, у збільшується на 1. Перше ніж розглядати наступний піксел, необхідно відкоректувати похибку відніманням від неї 1. Маємо e=1/4–1=-3/4. Помітимо, що перетин вертикальної прямої x=2 із заданим відрізком лежить на 1/4 нижче прямої у=1. Якщо ж перенести відрізок 1/2 вниз, ми одержимо саме величину -3/4. Продовження обчислень для наступного піксела дає e=-3/4+3/8=-3/8.
Тому що е від’ємне, то y не збільшується. З усього сказаного випливає, що похибка – це інтервал, що відтинається по осі y розглянутим відрізком у кожному растровому елементі (відносно -1/2).
Приведемо алгоритм Брезенхема для першого октанта, тобто для випадку 0£Dy£Dx.
Алгоритм Брезенхема розкладання в растр відрізка для першого октанта передбачається, що кінці відрізка (x1, y1) і (x2, y2) не збігаються.
Integer – функція перетворення в ціле
x, y, Dx, Dy – цілі
е – дійсне
ініціалізація змінних
x=x1
y=y1
Dx=x2-x1
Dy=y2-y1
Ініціалізація з виправленням на половину піксела
е=Dy/Dx-1/2
початок основного циклу
for i=1 to Dx
plot (x, y)
while (e=>0)
y=y+1
e=e-1
end while
x=x+1
e=e+Dy/Dx
next i
finish
Блок-схема алгоритму на рис. 3.3. Приклад наведений нижче.
Приклад 3.1. Алгоритм Брезенхема.
Розглянемо відрізок, проведений із точки (0,0) у точку (5,5). Розклад відрізка в растр по алгоритму Брезенхема приводить до такого результату:
початкові установки
x=0
y=0
Dx=5
Dy=5
е=1–1/2=1/2
Результати роботи покрокового циклу
| i | Plot | e | x | y |
| 1/2 | 0 | 0 | ||
| 1 | (0,0) | |||
| -1/2 | 0 | 1 | ||
| 1/2 | 1 | 1 | ||
| 2 | (1,1) | |||
| -1/2 | 1 | 2 | ||
| 1/2 | 2 | 2 | ||
| 3 | (2,2) | |||
| -1/2 | 2 | 3 | ||
| 1/2 | 3 | 3 | ||
| 4 | (3,3) | |||
| -1/2 | 3 | 4 | ||
| 1/2 | 4 | 4 | ||
| 5 | (4,4) | |||
| -1/2 | 5 | 5 | ||
| 1/2 | 5 | 5 |
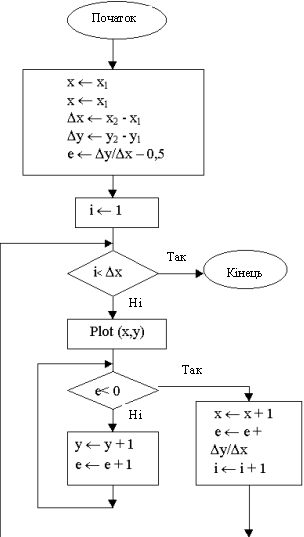
Блок-схема алгоритму Брезенхема
Результат показаний на рис. 3.4 і збігається з очікуваним. Помітимо, що точка растра з координатами (5,5) не активована. Цю точку можна активувати шляхом зміни циклу for-next на 0 to Dx. Активацію точки (0,0) можна усунути, якщо поставити оператор Plot безпосередньо перед рядком next i.
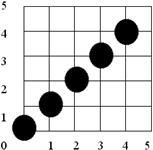
Результат роботи алгоритму Брезенхема в першому октанті
Похожие работы
... нужные пикселы труднее, что показано на рис. 1.1. Рис. 1.1 Разложение в растр отрезков прямых Прежде чем приступать к обсуждению конкретных алгоритмов рисования отрезков, полезно рассмотреть общие требования к таким алгоритмам и определить желаемые характеристики изображения. Очевидно, что отрезки должны выглядеть прямыми, начинаться и заканчиваться в заданных точках. Яркость вдоль отрезка должна ...
... + 1 надо подставить y = y - 1 end while finish Удаление невидимых линий и поверхностей Задача удаления невидимых линий и поверхностей является одной из наиболее сложных в машинной графике. Алгоритмыудаления невидимых линий и поверхностей служат для определения линий ребер, поверхностей или объемов, которые видимы или невидимы для наблюдателя, находящегося в заданной точке пространства. 3.1 ...
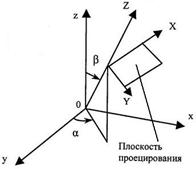
... Z можно отбросить. 2.1.6 Алгоритм Z-буфера После получения треугольников ландшафта (триангуляции равномерной сетки) и проецирования их на экранную плоскость следует построение изображения ландшафта. В процессе его построения для удаления невидимых поверхностей используется алгоритм Z-буфера. Это один из простейших алгоритмов удаления невидимых поверхностей. Работает этот алгоритм в ...
0 комментариев