Алгоритм Брезенхема для генерації кола

3. Алгоритм Брезенхема для генерації кола

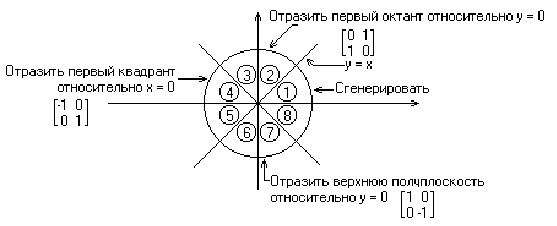
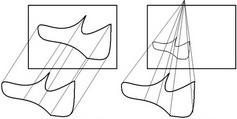
У растр потрібно розкладати не тільки лінійні, але й інші, більш складні функції. Розкладанню конічних перетинів, тобто кіл, еліпсів, парабол, гіпербол, було присвячено значне число робіт. Найбільша увага, зрозуміло, приділена колу. Один з найбільш ефективних і простих для розуміння алгоритмів генерації кола належить Брезенхему. Для початку відмітимо, що необхідно згенерувати тільки одну восьму частину кола. Інші його частини можуть бути отримані послідовними відображеннями, як це показано на рис. 5.1. Якщо згенерований перший октант (від 0 до 45° проти годинникової стрілки), то другий октант можна отримати дзеркальним відображенням відносно прямої y=х, що дає в сукупності перший квадрант. Перший квадрант відбивається відносно прямої х=0 для отримання відповідної частини кола в другому квадранті. Верхнє півколо відбивається відносно прямої y=0 для завершення побудови. На рис. 5.1 наведені двовимірні матриці відповідних перетворень.

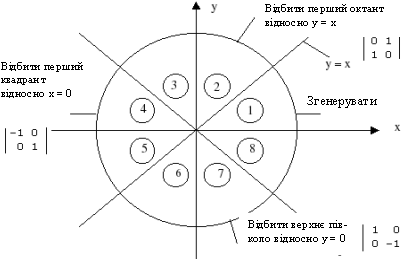
Генерація повного кола з дуги в першому октанті

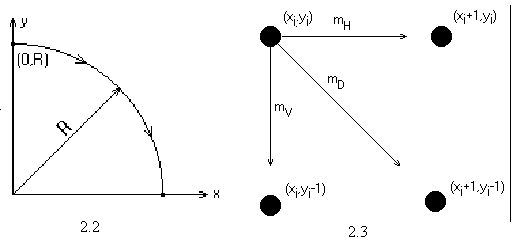
Для виведення алгоритму розглянемо першу чверть кола з центром у початку координат. Помітимо, що якщо робота алгоритму починається в точці х=0, у=R, то при генерації кола за годинниковою стрілкою в першому квадранті у є монотонно спадною функцією аргумента х (рис. 5.2). Аналогічно, якщо вихідною точкою є у=0, х=R, то при генерації кола проти годинникової стрілки х буде монотонно спадною функцією аргументу у. У нашому випадку вибирається генерація за годинниковою стрілкою з початком у точці х=0, у=R. Передбачається, що центр кола і початкова точка знаходяться точно в точках растра.

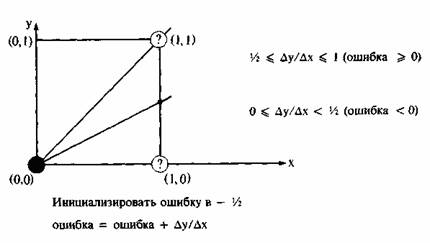
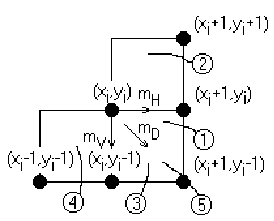
Для будь-якої заданої точки на колі при генерації за годинниковою стрілкою існує тільки три можливості вибрати наступний піксел, що щонайкраще наближає коло: горизонтально вправо, по діагоналі вниз і вправо, вертикально вниз. На рис. 5.3 ці напрямки позначені відповідно m_H, m_D, m_V. Алгоритм вибирає піксел, для якого мінімальний квадрат відстані між одним з цих положень і колом, тобто мінімум з

m_H=|(x_i+1)²+(y_i)²-R²|

m_D=|(x_i+1)²+(y_i-1)²-R²|

m_V=|(x_i)²+(y_i-1)²-R²|

Різниця між квадратами відстаней від центра кола до діагонального піксела (x_i+1, у_i-1) і від центра до точки на колі R² дорівнює

D_i=(x_i+1)²+(y_i-1)²-R²

Як і в алгоритмі Брезенхема для відрізка, для вибору відповідного піксела бажано використовувати тільки знак похибки, а не її величину.

При D_i<0 діагональна точка (x_i+1, у_i-1) знаходиться всередині реального кола, тобто це випадки 1 або 2 на рис. 5.4. Ясно, що в цій ситуації варто вибрати або піксел (x_i+1, у_i), тобто m_H, або піксел (x_i+1, у_i-1), тобто m_D. Для цього спочатку розглянемо випадок 1 і перевіримо різницю квадратів відстаней від кола до пікселів у горизонтальному і діагональному напрямках:

d=|(x_i+1)²+(y_i)²-R²|-|(x_i+1)²+(y_i-1)²-R²|

При d<0 відстань від кола до діагонального піксела більша, ніж до горизонтального. Навпаки, якщо d>0, відстань до горизонтального піксела більша. Таким чином,

при d<=0 вибираємо m_H (x_i+1, у_i)

при d>0 вибираємо m_D (x_i+1, у_i-1)

При d=0, коли відстань від кола до обох пікселів однакова, вибираємо горизонтальний крок.

Кількість обчислень, необхідних для оцінки величини d, можна скоротити, якщо помітити, що у випадку 1

(x_i+1)²+(y_i)²-R²>=0

(x_i+1)²+(y_i-1)²-R²<0

тому що діагональний піксел (x_i+1, у_i-1) завжди лежить всередині кола, а горизонтальний (x_i+1, у_i) – поза ним. Таким чином, d можна обчислити за формулою

d=(x_i+1)²+(y_i)²-R²+(x_i+1)²+(y_i-1)²-R²

Доповнення до повного квадрата члена (y_i)² за допомогою додавання і віднімання – 2y_i+1 дає

d=2 [(x_i+1)²+(y_i-1)²-R²]+2y_i-1

У квадратних дужках стоїть по визначенню D_i і його підстановка

d=2 (D_i+y_i) – 1

значно спрощує вираз.

Розглянемо випадок 2 на рис. 5.4 і помітимо, що тут повинен бути обраним горизонтальний піксел (x_i+1, у_i), тому що у є монотонно спадною функцією. Перевірка компонентів d показує, що

(x_i+1)²+(y_i)²-R²<0

(x_i+1)²+(y_i-1)²-R²<0

оскільки у випадку 2 горизонтальний (x_i+1, у_i) і діагональний (x_i+1, у_i-1) піксели лежать усередині кола. Отже, d<0, і при використанні того ж самого критерію, що й у випадку 1, вибирається піксел (x_i+1, у_i).

Якщо D_i>0, то діагональна точка (x_i+1, у_i-1) знаходиться поза колом, тобто це випадки 3 і 4 на рис. 5.4. У даній ситуації ясно, що потрібно вибрати піксел (x_i+1, у_i-1), або (x_i, у_i -1). Аналогічно розгляду попереднього випадку критерій вибору можна отримати, розглядаючи спочатку випадок 3 і перевіряючи різницю між квадратами відстаней від кола до діагонального m_D і вертикального m_V пікселів, тобто

d'=|(x_i+1)²+(y_i-1)²-R²|-|(x_i)²+(y_i-1)²-R²|.

При d'<0 відстань від кола до вертикального піксела (x_i, у_i -1) більша і варто вибрати діагональний крок до піксела (x_i+1, у_i-1). Навпаки, у випадку d'>0 відстань від кола до діагонального піксела більша і варто вибрати вертикальний рух до піксела (x_i, у_i-1). Таким чином, при d'<=0 вибираємо m_D (x_i+1, у_i-1), при d'>0 вибираємо m_V (x_i, у_i-1).

Тут для випадку d'=0, тобто коли відстані рівні, обраний діагональний крок.

Перевірка компонентів d' показує, що

(x_i)²+(y_i-1)²-R²>=0

(x_i+1)²+(y_i-1)²-R²<0

оскільки для випадку 3 діагональний піксел (x_i+1, у_i-1) знаходиться поза колом, тоді як вертикальний піксел (x_i, у_i-1) лежить всередині кола. Це дозволяє записати d' у вигляді

d'=(x_i+1)²+(y_i-1)²-R²+(x_i)²+(y_i-1)²-R²

Доповнення до повного квадрата члена (x_i)² за допомогою додавання і віднімання 2x_i+1 дає

d'=2 [(x_i+1)²+(y_i-1)²-R²]-2x_i-1

Використання визначення D_i приводить вираз до вигляду

d'=2 (D_i-x_i) – 1

Тепер, розглядаючи випадок 4, знову зауважимо, що варто вибрати вертикальний піксел (x_i, у_i-1), тому що y є монотонно спадною функцією від х.

Перевірка компонентів d' для випадку 4 показує, що

(x_i+1)²+(y_i-1)²-R²>0

(x_i)²+(y_i-1)²-R²>0

Оскільки обидва піксели знаходяться поза колом. Отже, d'>0 і при використанні критерію, розробленого для випадку 3, відбувається вірний вибір m_V.

Залишилося перевірити тільки випадок 5 на рис. 5.4, який зустрічається, коли діагональний піксел (x_i+1, у_i-1) лежить на колі, тобто D_i=0. Перевірка компонентів d показує, що

(x_i+1)²+(y_i)²-R²>0

(x_i+1)²+(y_i-1)²-R²=0

Отже, d>0 і вибирається діагональний піксел (x_i+1, у_i-1). Аналогічним чином оцінюємо компоненти d':

(x_i+1)²+(y_i-1)²-R²=0

(x_i+1)²+(y_i-1)²-R²<0

і d'<0, що є умовою вибору правильного діагонального кроку до (x_i+1, у_i-1). Таким чином, випадок D_i=0 підлягає тому ж критерію, що і випадок D_i<0 чи D_i>0. Підіб'ємо підсумок отриманих результатів:

D_i<0

d<=0 вибираємо піксел (x_i+1, у_i) – m_H

d>0 вибираємо піксел (x_i+1, у_i-1) – m_D

D_i>0

d'<=0 вибираємо піксел (x_i+1, у_i-1) – m_D

d'>0 вибираємо піксел (x_i, у_i-1) – m_V

D_i=0 вибираємо піксел (x_i+1, у_i-1) – m_D

Легко розробити прості рекурентні співвідношення для реалізації покрокового алгоритму. Спочатку розглянемо горизонтальний крок m_H до піксела (x_i+1, у_i). Позначимо це нове положення піксела як (i+1). Тоді координати нового піксела і значення D_i рівні

x_i+1=x_i+1

y_i+1=y_i

D_i+1=(x_i+1+1)²+(y_i+1-1)²-R²=D_i+2x_i+1+1

Аналогічно координати нового піксела і значення D_i для кроку m_D до піксела (x_i+1, у_i-1) такі:

x_i+1=x_i+1

y_i+1=y_i-1

D_i+1=D_i+2x_i+1-2y_i+1+2

Те ж саме для кроку m_V до (x_i, у_i-1)

x_i+1=x_i

y_i+1=y_i-1

D_i+1=D_i-2y_i+1+1

Реалізація алгоритму Брезенхема на псевдокоді для кола наводиться нижче.

Покроковий алгоритм Брезенхема для генерації кола в першому квадранті усі змінні – цілі ініціалізація змінних

x_i=0

y_i=R

D_i=2 (1-R)

Межа=0

1 Plot (x_i, y_i)

if y_i<=Межа then 4

Виділення випадку 1 чи 2, 4 чи 5, чи 3

if D_i<0 then 2

if D_i>0 then 3

if D_i=0 then 20

визначення випадку 1 чи 2

2d=2D_i+2у_i-1

if d<=0 then 10

if d>0 then 20

визначення випадку 4 чи 5

3d=2D_i+2х_i-1

if d<=0 then 20

if d>0 then 30

виконання кроків

крок до m

10х_i=х_i+1

D_i=D_i+2х_i+1

gо to 1

крок m

20х_i=х_i+1

y_i=y_i+1

D_i=D_i+2х_i-2у_i+2

gо to 1

4 finish

Змінна межі встановлюється в нуль для закінчення роботи алгоритму на горизонтальній осі, в результаті генерується коло у першому квадранті. Якщо необхідний лише один з октантів, то другий октант можна отримати за допомогою установки Межа=Integer (R/sqrt(2)), а перший – за допомогою відображення другого октанта відносно прямої у=х (рис. 5.1). Блок-схема алгоритму показана на рис. 5.5.

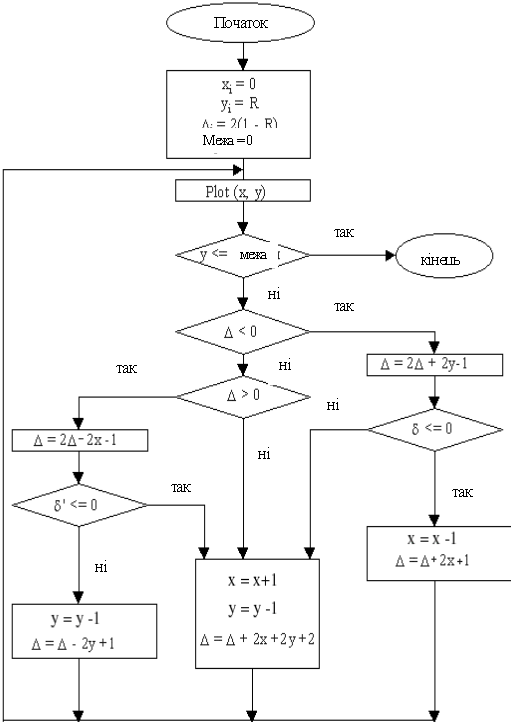
Блок-схема покрокового алгоритму Брезенхема для генерації кола в першому квадранті

Розглянемо коло радіусом 8 з центром в початку координат. Генерується тільки перший квадрант.

x=0

y=8

=2 (1–8)=-14

Межа=0

Покрокове виконання основного циклу

1 Plot (0,8)

yi>Межа (продовжувати)

Di<0 go to 2

2d=2 (-14)+2 (8) – 1=-13<0 go to 10

10x=0+1=1

Di=-14+2+1=-11

go to 1

1 Plot (1,8)

yi>Межа (продовжувати)

Di<0 go to 2

2d=2 (-11)+2 (8) – 1=-7<0 go to 10

10x=1+1=1

Di=-11+2 (2)+1=-6

go to 1

1 Plot (2,8)

Результати всіх послідовних проходів алгоритму зведені в таблицю. Список пікселів обраних алгоритмів складається з (0,8), (1,8), (2,8), (3,7), (4,7), (5,6), (6,5), (7,4), (7,3), (8,2), (8,1), (8,0).

Plot	Di	d	d'	x	y
	-14			0	8
(0,8)
	-11	-13		0	8
(1,8)
	-6	-7		2	8
(2,8)
	-12	3		3	7
(3,7)
	-3	11		4	7
(4,7)
	1	5		6	5
(6,5)
	9		-11	7	4
(7,4)
	18		-7	8	2
(8,2)
	17		19	8	1
(8,1)
	18		17	8	0
(8,0)

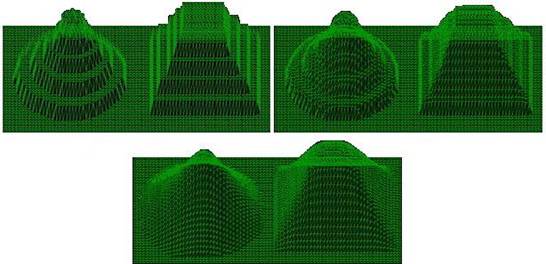
Результати показані на рис. 5.6. разом з реальним колом. Алгоритм легко узагальнюється для інших квадрантів чи дуг кіл.

алгоритм генерація коло брезенхем

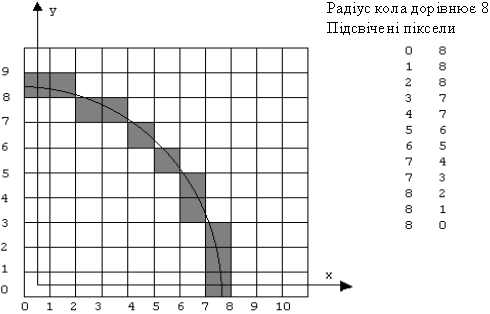
Результати роботи покрокового алгоритму Брезенхема генерації кола