Навигация
Загальний алгоритм Брезенхема
2. Загальний алгоритм Брезенхема
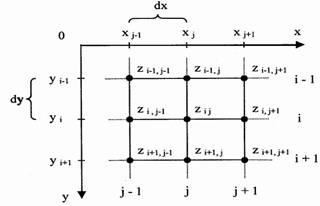
Щоб реалізація алгоритму Брезенхема була повною необхідно розглянути відрізки у всіх октантах. Модифікацію легко зробити, враховуючи в алгоритмі номер квадранта, в якому лежить відрізок і його кутовий коефіцієнт. Коли абсолютна величина кутового коефіцієнта більше 1, у постійно змінюється на одиницю, а критерій похибки Брезенхема використовується для ухвалення рішення про зміну величини x. Вибір постійно змінюваної координати (на +1 чи -1) залежить від квадранта (рис. 4.1.). Загальний алгоритм може бути оформлений у наступному вигляді:
Узагальнений цілочисельний алгоритм Брезенхема квадрантів передбачається, що кінці відрізка (x1, y1) і (x2, y2) не збігаються усі змінні вважаються цілими Sign – функція, що повертає -1, 0, 1 для від’ємного, нульового і додатнього аргумента відповідно ініціалізація змінних
x=x1
y=y1
Dx=abs (x2-x1)
Dy=abs (y2-y1)
s1=Sign (x2-x1)
s2=Sign (y2-y1)
обмін значень Dx і Dy в залежності від кутового коефіцієнта нахилу відрізка
if Dy<Dx then
Temp=Dx
Dx=Dy
Dy=Temp
Обмін=1
else
Обмін=0
end if
ініціалізація e з виправленням на половину піксела
e=2*Dy-Dx
основний цикл
for i=1 to Dx
Plot (x, y)
while (e=>0)
if Обмін=1 then
x=x+s1
else
y=y+s2
end if
e=e-2*Dx
end while
if Обмін=1 then
y=y+s2
else
x=x+s1
end if
e=e+2*Dy
next i
finish
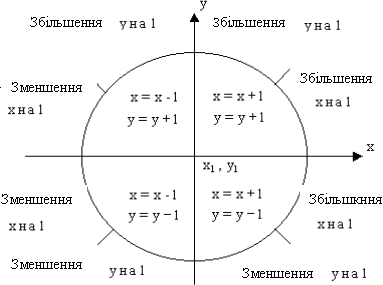
Розгляд випадків для узагальненого алгоритму Брезенхема
Для ілюстрації розглянемо відрізок із точки (0, 0) у точку (-8, -4).
початкові установки
x=0
y=0
Dx=8
Dy=4
s1=-1
s2=-1
Обмін=0
е=0
Результати роботи покрокового циклу
| i | Plot | е | x | y |
| 0 | 0 | 0 | ||
| 1 | (0,0) | |||
| -16 | 0 | -1 | ||
| -8 | -1 | -1 | ||
| 2 | (-1, – 1) | |||
| 0 | -2 | -1 | ||
| 3 | (-2, – 1) | |||
| -16 | -2 | -2 | ||
| -8 | -3 | -2 | ||
| 4 | (-3,2) | |||
| 0 | -4 | -2 | ||
| 5 | (-4,2) | |||
| -16 | -4 | -3 | ||
| -8 | -5 | -3 | ||
| 6 | (-5, – 3) | |||
| 0 | -6 | -3 | ||
| 7 | (-6, – 3) | |||
| -16 | -6 | -4 | ||
| -8 | -7 | -4 | ||
| 8 | (-7, – 4) | |||
| 0 | -8 | -4 |
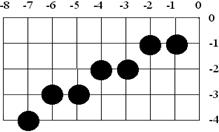
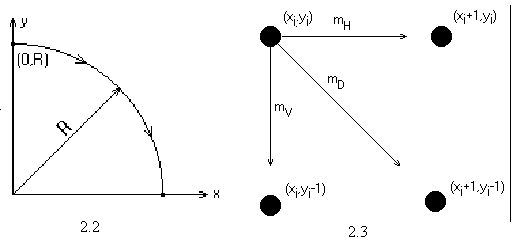
Результат роботи узагальненого алгоритму Брезенхема в третьому квадранті
На рис. 4.2 показаний результат. Порівнюючи з рис. 2.2 бачимо, що результати роботи двох алгоритмів відрізняються.
Похожие работы
... нужные пикселы труднее, что показано на рис. 1.1. Рис. 1.1 Разложение в растр отрезков прямых Прежде чем приступать к обсуждению конкретных алгоритмов рисования отрезков, полезно рассмотреть общие требования к таким алгоритмам и определить желаемые характеристики изображения. Очевидно, что отрезки должны выглядеть прямыми, начинаться и заканчиваться в заданных точках. Яркость вдоль отрезка должна ...
... + 1 надо подставить y = y - 1 end while finish Удаление невидимых линий и поверхностей Задача удаления невидимых линий и поверхностей является одной из наиболее сложных в машинной графике. Алгоритмыудаления невидимых линий и поверхностей служат для определения линий ребер, поверхностей или объемов, которые видимы или невидимы для наблюдателя, находящегося в заданной точке пространства. 3.1 ...
... Z можно отбросить. 2.1.6 Алгоритм Z-буфера После получения треугольников ландшафта (триангуляции равномерной сетки) и проецирования их на экранную плоскость следует построение изображения ландшафта. В процессе его построения для удаления невидимых поверхностей используется алгоритм Z-буфера. Это один из простейших алгоритмов удаления невидимых поверхностей. Работает этот алгоритм в ...
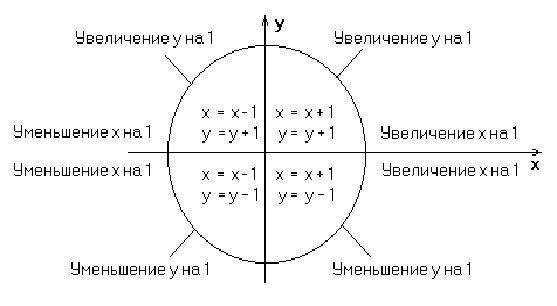
0 комментариев