2. Динамические ошибки в системах авторегулирования
Системы автоматического регулирования всегда находятся под влиянием двух видов воздействий: задающего и возмущающего. Задающее воздействие определяет, каким должен быть выходной процесс, и оно единственное. Возмущающих воздействий может быть много и прикладываются они к различным точкам системы, но в линейных системах всех их можно привести к входу и заменить одним, более или менее сложным, возмущающим воздействием.
В следящей системе требуется, чтобы выходной процесс y(t) совпадал с задающим воздействием xз(t). Разница между ними является ошибкой δ(t) = xз(t) – y(t). Модель для расчета ошибки приведена на рис. 23.











Рис. 23
Изображение ошибки
Δ(p) = Xз(p) – Y(p) = Xз(p) – [Xз(p) + Xв(p)]Kз(р) =
= [1 –Kз(p)]Xз(p) – Kз(p)Xв(p) = Kош(p)Xз(p) – Kз(p)Xв(p). (10)
Как видим, ошибка состоит из двух составляющих. Первая зависит от задающего воздействия и будет отсутствовать, если Кз(jω) = 1 во всем диапазоне частот, занятых спектром задающего воздействия. На практике частотная характеристика Кз(jω) отличается от 1 в области верхних частот. Значит, будут с ошибкой отрабатываться высокочастотные изменения задающего воздействия, и ошибка поэтому называется динамической. Вторая составляющая связана с возмущающим воздействием и появляется, если в области частот, занятых спектром возмущающего воздействия, АЧХ замкнутой системы будет отлична от нуля.
Ошибка может определяться при самых разнообразных задающем и возмущающем воздействиях. Обычно воздействие берется одним из типовых: скачкообразным, гармоническим, полиномиальным или стационарным случайным процессом. Рассмотрим ошибки при двух последних воздействиях.
Если задающее воздействие является медленно меняющимся процессом, то в течение некоторого временного интервала его можно описать полиномом: xз(t) = α0 + α1t + α2t2 +… Ошибку удобно представить в виде ряда по производным входного воздействия:
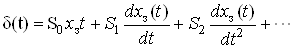 ,
,
где коэффициенты Si определяются по передаточной функции ошибки Кош(p):
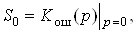
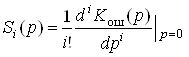 .
.
Если S0 ≠ 0, система называется статической, если S0 = 0, – астатической. Число первых нулевых коэффициентов определяет порядок астатизма.
Ниже в таблице приведены выражения для первых трех коэффициентов для систем с различными передаточными функциями Кр(р).
| Тип системы | Статическая | Астатическая
1-го порядка | Астатическая
2-го порядка |
| Kp(p) | K  (1+p)(1+pT) (1+p)(1+pT)
| K  p(1+pT) p(1+pT)
| K(1+p)  P2(1+pT) P2(1+pT)
|
| S0 | 1  1+K 1+K
| 0 | 0 |
| S1 | K(1+T)  (1+K)2 (1+K)2
| 1  K K
| 0 |
| S2 | K[(1+K)T-(1+T)2]  (1+K)3 (1+K)3
| KT – 1  K2 K2
| 1  K K
|
Практический интерес представляют ошибки для каждого из слагаемых полиномиального воздействия. Если воздействие постоянно (xз = =x0), то ошибку называют статической δст; если xз(t) = Vxt, – скоростной δск, а при xз(t)=аxt2/2 – ошибкой по ускорению δуск. Так как эти воздействия имеют конечное количество производных, то ошибки определяются первыми членами ряда:
δст = S0x0,
δск = S0Vxt + S1Vx,
(11)
δуск = S0axt2/2 + S1axt + S2ax.
Для расчета этих ошибок надо знать только три первых коэффициента.
На рис. 24 показано, как отрабатываются постоянное и линейное воздействия в статической и астатических системах. Видим, что статическая система обладает наибольшими ошибками. Чем выше порядок астатизма, тем точнее система отрабатывает полиномиальное воздействие.
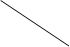










Рис. 24
Рассмотрим теперь ошибки при случайных воздействиях. Задающее воздействие описывается медленно меняющимся случайным процессом, спектральная плотность Sxз(ω) которого сосредоточена в области низких частот. Возмущающее воздействие является широкополосным процессом со спектральной плотностью Sxв(ω), и его часто считают белым шумом. Если задающее и возмущающее воздействия некоррелированы, то в соответствии с выражением (10) энергетический спектр динамической ошибки
Sдин(ω) = Sxз(ω)|Кош(jω)|2.
Дисперсия динамической ошибки
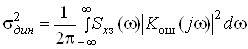 .
.
Дисперсия ошибки по возмущению
 .
.
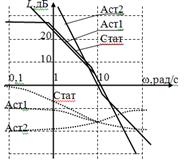
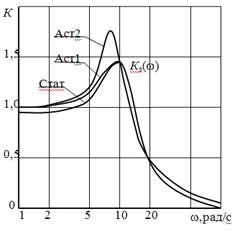
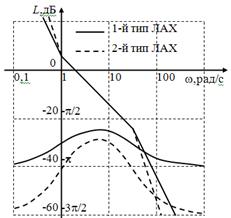
Рассмотрим, как влияет тип системы (статическая или астатическая) на ошибки при случайных воздействиях. На рис. 25,а изображены ЛАХ и ЛФХ разомкнутой системы для трех типов систем, передаточные функции которых приведены в таблице. Эти характеристики различаются лишь в области нижних частот, а в области средних и верхних частот одинаковы. Если коэффициент передачи разомкнутой системы К достаточно большой, то

и АЧХ замкнутой системы для всех трех типов будут близки друг к другу (см. рис. 25,б). Следовательно, статическая и астатические системы будут иметь примерно одинаковые ошибки.

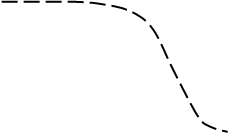
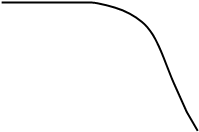























Рис. 25
Как правило, изменение какого-либо параметра системы (коэффициента передачи К или постоянной времени Т) приводит к противоположному изменению дисперсий динамической ошибки и ошибки по возмущению. Рассмотрим это на примере астатической системы первого порядка.
Допустим, задающее воздействие формируется из белого шума с спектральной плотностью Sз0 пропусканием его через интегрирующую цепь с постоянной времени Tx. Тогда дисперсия задающего воздействия
автоматический регулирование передача
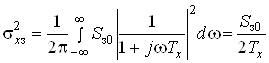 .
.
Для расчета дисперсии динамической ошибки нужно знать частотную характеристику ошибки Кош(jω):
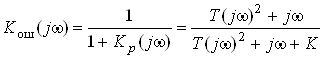 .
.
Дисперсия динамической ошибки:
 .
.
Вводя относительные величины α = 1/Tx и β = T/Tx и учитывая выражение для дисперсии задающего воздействия, получаем:
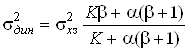 . (12)
. (12)
Видим, что при К = 0 дисперсия динамической ошибки равна дисперсии задающего воздействия. Это объясняется тем, что при К = 0 выходной процесс y(t) = 0 и ошибка становится равной задающему воздействию. С увеличением коэффициента передачи К дисперсия уменьшается и стремится к постоянной величине, равной β. На первый взгляд может показаться, что получен результат, противоречащий здравому смыслу. Ведь с увеличением коэффициента передачи разомкнутой системы расширяется полоса пропускания замкнутой системы, значит, должны лучше отрабатываться высокочастотные составляющие задающего воздействия, и ошибка должна стремиться к нулю. Но никакого противоречия нет. Результат объясним, если учесть форму частотной характеристики ошибки. С увеличением К уменьшается запас устойчивости по фазе и, следовательно, увеличивается подъем АЧХ замкнутой системы в области верхних частот. А так как Кош(jω) = 1 – Кз(jω), то уменьшение спектральной плотности задающего воздействия компенсируется увеличением модуля частотной характеристики ошибки.
Дисперсия ошибки по возмущению при условии, что возмущающее воздействие является белым шумом со спектральной плотностью Sв0, равна:
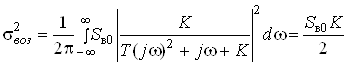 .
.
Дисперсия пропорциональна коэффициенту передачи разомкнутой системы и не зависит от постоянной времени Т. Это объясняется следующим образом. При малом К, когда К < 1/T, частота среза равна К и полоса пропускания замкнутой системы растет пропорционально К. Когда К > 1/T, частота среза увеличивается в меньшей степени, чем растет К, но из-за уменьшения запаса устойчивости по фазе в АЧХ замкнутой системы появляется подъем в области верхних частот. Это иллюстрируется частотными характеристиками, представленными на рис. 26. Площадь под |Кз(jω)|2 остается неизменной, а именно она определяет дисперсию ошибки по возмущению.
Дисперсия суммарной ошибки при некоррелированных задающем и возмущающем воздействиях σ2Σ = σ2дин + σ2воз. Зависимость дисперсий





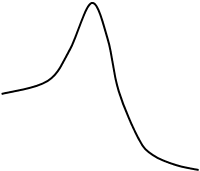
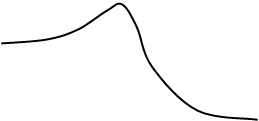



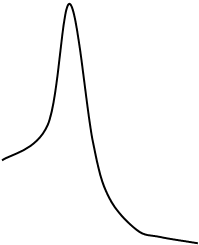














Рис. 26
ошибок от коэффициента передачи К приведена на рис. 27.Видим, что существует оптимальный коэффициент передачи К, при котором дисперсия суммарной ошибки минимальна, хотя этот оптимум не очень ярко выражен и при изменении коэффициента передачи в 2 раза дисперсия практически не изменяется. Если задающее и возмущающее воздействия коррелированы, то при расчете ошибок нужно учесть составляющие, связанные с взаимными энергетическими спектрами воздействий.
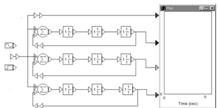
Исследование проводится параллельно на трех идентичных моделях (рис. 28). Модель содержит два линейных звена, задаваемых передаточными функциями. Передаточную функцию второго звена принять равной К/(1 + pT), а первого – в зависимости от типа системы: для статической – 1/(1 + p), для астатической первого порядка – 1/p, для астатической второго порядка – (1 + р)/p2.
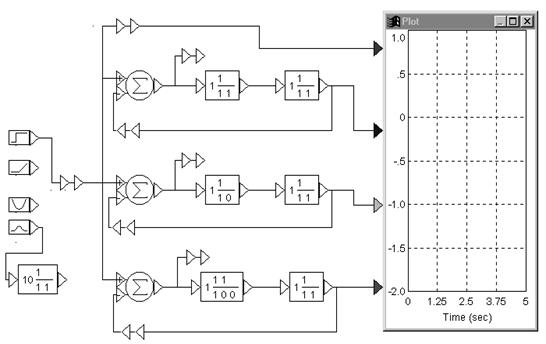
Рис. 28
На вход системы можно подать любое из воздействий: постоянное, линейное, квадратичное или узкополосный случайный процесс, подсоединив выход соответствующего блока к входу системы.
Заключение
Формирование систем автоматического регулирования, как правило, выполняют на основе аналитических методов анализа или синтеза. На этом этапе проектирования систем регулирования на основе принятые допущений составляют математическую модель системы и выбирают предварительную ее структуру. В зависимости от типа модели (линейная или нелинейная) выбирают метод расчета для определения параметров, обеспечивающих заданные показатели устойчивости, точности и качества. После этого уточняют математическую модель и с использованием средств математического моделирования определяют динамические процессы в системе. При действии различных входных сигналов снимают частотные характеристики и сравнивают с расчетными. Затем окончательно устанавливают запасы устойчивости системы по фазе и модулю и находят основные показатели качества.
Далее, задавая на модель типовые управляющие воздействия; снимают характеристики точности. На основании математического моделирования составляют технические требования на аппаратуру системы. Из изготовленной аппаратуры собирают регулятор и передают его на полунатурное моделирование, при котором объект регулирования набирают в виде математической модели.
Развитие теории автоматического регулирования на основе уравнений состояния и z-преобразований, принципа максимума и метода динамического программирования совершенствует методику проектирования систем регулирования и позволяет создавать высокоэффективные автоматические системы для самых различных отраслей народного хозяйства. Полученные таким образом системы автоматического регулирования обеспечивают высокое качество выпускаемой продукции, снижают ее себестоимость и увеличивают производительность труда.
Список литературы:
1. Коновалов Г.Ф. Радиоавтоматика: Учебник для вузов. М.: Радиотехника, 2003. 288 с.
2. Первачев С.В. Радиоавтоматика: Учебник для вузов. М.: Радио и связь, 1982. 296 с.
3. Радиоавтоматика: Учебное пособие / Под ред. В.А.Бесекерского. М.: Высшая школа, 1985.271 с.
4. Системы радиоавтоматики и их модели: Учеб. пособие / Ю.Н.Гришаев; Рязан. радиотехн. институт. Рязань, 1977. 46 с.
5. Шахгильдян В.В., Ляховкин А.А. Системы фазовой автоподстройки частоты. М.: Связь, 1972.448 с.
6. Синтез частотных характеристик линейных систем автоматического регулирования: Метод. указания / Рязан. гос. Радиотехн.акад.; Сост. Ю.Н.Гришаев. Рязань, 2000. 12 с.
Раздел:
Коммуникации и связь Количество знаков с пробелами: 17506
Количество таблиц: 1
Количество изображений: 12
... Рис. 6 Рис. 7 Схема моделирования показана на рис. 8. Рис.8 Исследование устойчивости для удобства сравнения проводится на трех моделях, отличающихся структурой или параметрами. 2.Оптимальные линейные САР Задача оптимального синтеза линейной системы авторегулирования при случайных воздействиях заключается в определении такой структуры и параметров системы, при ...
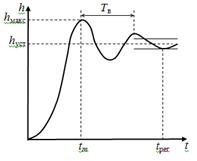
... частот, то переходная характеристика будет колебательной. Переходная характеристика является показателем качества при быстро изменяющемся воздействии. Для систем авторегулирования лучшей считается колебательная переходная характеристика с быстрым затуханием колебаний на вершине (рис. 4). Рис. Обычно используются следующие числовые параметры переходной характеристики: время достижения ...
... и сигнализация нарушений и аварийных ситуаций с их протоколированием; Возможность дистанционного управления регулирующими исполнительными механизмами; Надежность.
Для более
эффективного
функционирования
системы автоматизации
можно предъявить
к Scada-пакету следующие
требования: Контроль над технологическим процессом, состояние технологического оборудования и управление процессами и ...
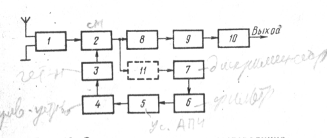
... ; 7-дикриминатор; 8- УПЧ; 9- детектор сигнала; 10-УНЧ; 11-усилитель промежуточной частоты АПЧ (может и отсутствовать) Структурная схема и принцип действия систем АПЧ. Системы АПЧ супергетеродинных приемников относятся к числу автоматических регулировок обратного действия. Возможны два вида автоматической подстройки частоты: частотная (которую принято называть АПЧ) и фазовая (ФАПЧ). Первый ...
![]()



![]() ,
,![]()
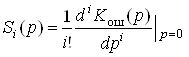 .
.


![]() .
.![]() .
.






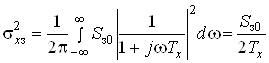 .
.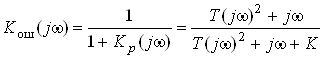 .
. .
.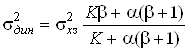 . (12)
. (12)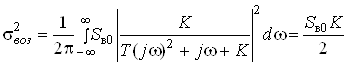 .
.![]()








 Рис. 28
Рис. 28 

0 комментариев