Критерий оптимальности задается диаметрально противоположным критерию прямой задачи

2.  Критерий оптимальности задается диаметрально противоположным критерию прямой задачи.

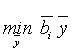
3.  Система ограничений двойственной задачи получается, если заданную матрицу A_i умножить слева на вектор новых переменных , в качестве вектора констант ограничений взять вектор коэффициентов  целевой функции прямой задачи, а знак неравенства поменять на противоположный.

Полученная двойственная задача линейного программирования

;

;

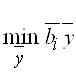ti	400	500	700	800	1000
Цi1	210	180	190	200	170
Цi2	190	170	160	150	240

		I	II
	K1	16 135	16 247
	K2	9 679	10 339
	K3	8 758	7 001
	K4	9 009	5 348
	K5	5 942	13 866
	b1=	700 000,00
	D=	9 000 000,00
Sij	400	14 668	18 053
	500	12 099	14 769
	700	9 731	11 668
	800	9 009	10 695
	1000	8 489	9 904

	D-Зпостi	Тгодi	Зпостi
1	6 868 067	700 000	2 131 933
2	6 422 291	700 000	2 577 709

400x1+500x2+700x3+800x4+1000x5<=700000
14668x1+12099x2+9731x3+9009x4+8489x5<=6868067
16135x1+9679x2+8758x3+9009x4+5942x5<=2131933
400y1+14668y2=16135
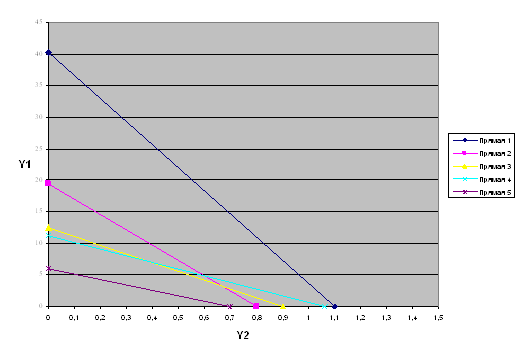
F(A) = 28236728	y2=0	y1=40,34
F(C) =7554874	y1=0	y2=1,1
x1=	468
x1=	1750
400x1+500x2+700x3+800x4+1000x5<=700000
18053x1+14769x2+11668x3+10695x4+9904x5<=6422291
16247x1+10339x2+7001x3+5348x4+13866x5=2577709
	400y1+18052,59y2=16247,33
	F(A) =28432824	y2=0	y1=40,62
	400y1+18052,59y2=16247,33
	1000y1+ 9903,97y2=13865,55
	F(B) = 9318210	y2 = 0,76	y1= 6,34
	1000y1+ 9903,97y2=13865,55
	F(C) =8991207
	x5=	700
	x5=	648

Определение оптимальной стратегии производства в условиях неопределенности цен на ресурсы и готовую продукцию

При каждом i-ом уровне цен:

решая задачу линейного программирования

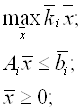
можно получить соответствующие оптимальные программы выпуска изделий

обеспечивающие максимальные прибыли при каждом i-ом состоянии «внешней среды»

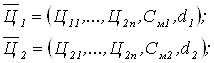
которым соответствуют две оптимальные стратегии выпуска продукции

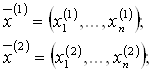
обеспечивающие в каждом отдельном случае максимальную прибыль

Ставится задача определить оптимальную стратегию выпуска продукции

,

обеспечивающую максимальную гарантированную прибыль в условиях неопределенности состояния «внешней среды».

Построение матричной игры с «внешней средой»

Сформулированная задача может быть разрешена с помощью теории матричных (стратегических) игр, для чего необходимо составить матрицу возможных прибылей

Таблица 19. Матрица возможных прибылей

	Ц1	Ц2
х1	3 608 264,72	3 202 352,70
х2	1 721 423,48	6 413 498,14

Из матрицы возможных прибылей следует.

1. Если будет реализована чистая стратегия производства , то в зависимости от состояния «внешней среды» прибыль предприятия будет составлять:

-  либо  при уровне цен ;

-  либо  при уровне цен ;

Прибыль

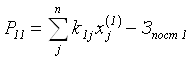
определяется решение М  задачи

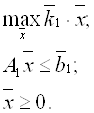
При этом трудоемкость годовой программы выпуска продукции равняется:

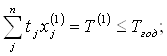
а производственные затраты составляют

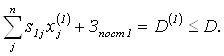
Прибыль определяется как

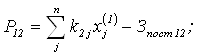
при условии, что производственные затраты не превышают расчетную величину

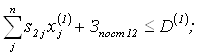
Если же ограничения по производственным затратам не выполняются, то прибыль рассчитывается как

;

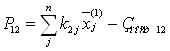где:

В этом случае трудоемкость годовой программы выпуска продукции будет равняться

2. Если будет реализована чистая стратегия производства , то в зависимости от состояния «внешней среды» прибыль предприятия будет составлять:

-  либо  при уровне цен ;

-  либо  при уровне цен ;

Прибыль

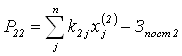
определяется решением  задачи линейного программирования

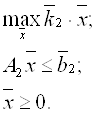
При этом трудоемкость годовой программы выпуска продукции равна

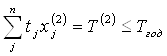
а производственные затраты составляют

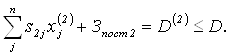
Прибыль  определяется как

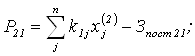
при условии, что производственные затраты не превышают расчетную величину

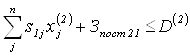
Если же ограничение по производственным затратам не выполняется, то прибыль рассчитывается как

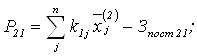
где:

В этом случае трудоемкость годовой программы выпуска продукции будет составлять:

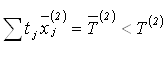
Полученные результаты сводятся в таблицу №20, где  – косвенные затраты соответствующие к-му масштабу производства при i-ом состоянии «внешней среды».

Ставится задача найти такое долевое распределение ресурсов  между чистыми стратегиями производства  при котором независимо от возможного уровня цен  гарантированная прибыль была бы максимальной. Если принять допущение, что прибыли предприятия пропорциональны объемам производства, а те в свою очередь пропорциональны выделенным ресурсам, то для решения поставленной задачи необходимо решить сформулированную матричную игру, т.е. определить цену игры  и обеспечивающую ее оптимальную стратегию

где:

Для решения этой задачи необходимо определить нижнюю  и верхнюю  цену игры

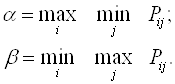
Безрисковая стратегия

р2 =	0,08
р1 =	0,92

В случае равенства нижней и верхней цены игры, что соответствует наличию седловой точки в рассматриваемой матричной игре, цена игры (g) – гарантированный максимальный результат – определяется одной из чистых стратегий , доставляющей максимальный результат из наихудших возможных исходов

При этом

Если нижняя и верхняя цены игры не равны между собой: ; то для обеспечения максимального гарантированного результата должны выполняться следующие соотношения

которые представляют собой систему трех линейных уравнений с тремя неизвестными . Найденное решение  трактуется как долевое распределение производственных ресурсов между оптимальными чистыми стратегиями производства  и определяет собой смешанную стратегию выпуска продукции  в объемах

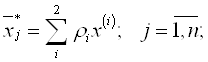
которые гарантируют получение прибыли в размере

	1-й	2-й
y =	3458030,60	3458033,60

Таким образом, получим безрисковую стратегию производства

обеспечивающую наибольшую гарантированную прибыль в условиях неопределенности цен на ресурсы и готовую продукцию.

х5*=	468
х1*=	648
x1		x5
327		52

Заключение

В заключение выполняемого проекта, исходя из полученной годовой программы выпуска продукции , рассчитываются основные технико-экономические характеристики деятельности рассматриваемого предприятия, которые сводятся в таблицу №21

Таблица 21. Технико-экономические показатели деятельности предприятия

Наименование показателя	Индекс уровня цен i={1,2}	Индекс изделия		Суммарное значение показателя
		1	5
Кол-во изделий (шт.)	−	365	116	−
Трудоемкость производства (нормо-ч.)	−	145884,86	115955,22	182602,89
Количество стапелей общей сборки (шт.)	−	3	3	−
Количество стеллажей внестапельной доработки (шт.)	−	−	−	5
Количество приспособлений для узловой и панельной сборки (шт.)	−	7	7	−
Количество сверлильно-зенковального и клепального оборудования (шт.)	−	−	−	4
Количество основных производственных рабочих (чел.)	−	−	−	92
Количество вспомогательных рабочих, руководителей, специалистов и МОП (чел.)	−	−	−	74
Прямые затраты на одно изделие (грн./изд.)	1	14668,87	8490,18	−
	2	18052,98	9904,96
Косвенные расходы (грн.)	1	−	−	966110,12
	2	−	−	1267325,43
Процент косвенных расходов от годового фонда ПЗП основных рабочих	1	−	−	199,52
	2	−	−	290,80
Цена изделия (грн./изд.)	1	30804,63	14433,30	−
	2	32495,37	23771,91	−
Себестоимость изделия (грн./изд.)	1	16785,18	13780,95	−
	2	18053,00	9904,97	−
Доход [грн.]	1	11234822,65	1673617,04	12908439,68
	2	11851456,65	2756476,76	14607933,41
Затраты [грн.]	1	6121758,95	1597973,17	7300506,27
	2	6584148,91	1148532,79	9000000,00
Прибыль [грн.]	1	5113063,70	75643,86	5607933,41
	2	5267307,74	1607943,97	5607933,41

где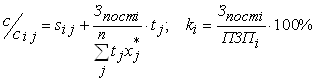

 – годовой фонд прямой заработной платы основных производственных рабочих при i-ом состоянии «внешней среды».

Литература

1.  Технико-экономическое проектирование цехов: Учеб. пособие / Константинов Ю.С., Никитин С.А., Попов Е.Н., Сафронов Я.В. – Харьков, 1988 г.

2.  Технико-экономическое обоснование предпринимательских проектов / В.Н. Гавва, Я.В. Сафронов. – Харьков, 1995 г.

3.  Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. М., – «Высшая школа», 1976 г.