Навигация
В соответствии с условиями его применения необходимо пользоваться следующим соотношением
1. В соответствии с условиями его применения необходимо пользоваться следующим соотношением
![]()
где
![]() .
.
2. Условия применения критерия предусматривают, что теоретическая функция распределения известна полностью – известны вид функции и значения ее параметров. На практике параметры обычно неизвестны и оцениваются по ЭД. Но критерий не учитывает уменьшение числа степеней свободы при оценке параметров распределения по исходной выборке. Это приводит к завышению значения вероятности соблюдения нулевой гипотезы, т.е. повышается риск принять в качестве правдоподобной гипотезу, которая плохо согласуется с ЭД (повышается вероятность совершить ошибку второго рода). В качестве меры противодействия такому выводу следует увеличить уровень значимости a, приняв его равным 0,1 – 0,2, что приведет к уменьшению зоны допустимых отклонений.
Критерий Р. Мизеса
В качестве меры различия теоретической функции распределения F(x) и эмпирической Fn(x) по критерию Мизеса (критерию w2) выступает средний квадрат отклонений по всем значениям аргумента x
![]() (3.9)
(3.9)
Статистика критерия
![]() (3.10)
(3.10)
При неограниченном увеличении n существует предельное распределение статистики nwn2. Задав значение вероятности a можно определить критические значения nwn2(a). Проверка гипотезы о законе распределения осуществляется обычным образом: если фактическое значение nwn2 окажется больше критического или равно ему, то согласно критерию Мизеса с уровнем значимости a гипотеза НО о том, что закон распределения генеральной совокупности соответствует F(x), должна быть отвергнута.
Достоинством критерия Мизеса является быстрая сходимость к предельному закону, для этого достаточно не менее 40 наблюдений в области часто используемых на практике больших значений nwn (а не несколько сот, как для критерия хи-квадрат).
Сопоставляя возможности различных критериев, необходимо отметить следующие особенности. Критерий Пирсона устойчив к отдельным случайным ошибкам в ЭД. Однако его применение требует группирования данных по интервалам, выбор которых относительно произволен и подвержен противоречивым рекомендациям. Критерий Колмогорова слабо чувствителен к виду закона распределения и подвержен влиянию помех в исходной выборке, но прост в применении. Критерий Мизеса имеет ряд общих свойств с критерием Колмогорова: оба основаны непосредственно на результатах наблюдения и не требуют построения статистического ряда, что повышает объективность выводов; оба не учитывают уменьшение числа степеней свободы при определении параметров распределения по выборке, а это ведет к риску принятия ошибочной гипотезы. Их предпочтительно применять в тех случаях, когда параметры закона распределения известны априори, например, при проверке датчиков случайных чисел.
При проверке гипотез о законе распределения следует помнить, что слишком хорошее совпадение с выбранным законом распределения может быть обусловлено некачественным экспериментом («подчистка» ЭД) или предвзятой предварительной обработкой результатов (некоторые результаты отбрасываются или округляются).
Выбор критерия проверки гипотезы относительно произволен. Разные критерии могут давать различные выводы о справедливости гипотезы, окончательное заключение в таком случае принимается на основе неформальных соображений. Точно также нет однозначных рекомендаций по выбору уровня значимости.
Рассмотренный подход к проверке гипотез, основанный на применении специальных таблиц критических точек распределения, сложился в эпоху "ручной" обработки ЭД, когда наличие таких таблиц существенно снижало трудоемкость вычислений. В настоящее время математические пакеты включают процедуры вычисления стандартных функций распределений, что позволяет отказаться от использования таблиц, но может потребовать изменения правил проверки. Например, соблюдению гипотезы Н0 соответствует такое значение функции распределения критерия, которое не превышает значение доверительной вероятности 1–a (оценка статистики критерия соответствует доверительному интервалу). В частности, для примера 3.1 значение статистики критерия хи-квадрат равно 1,318. А значение функции распределения хи-квадрат для этого значения аргумента при трех степенях свободы составляет 0,275, что меньше доверительной вероятности 0,95. Следовательно, нет оснований отвергать нулевую гипотезу.
Задание 2
Задача. Рассчитайте среднее арифметическое и среднее квадратическое отклонения и коэффициенты вариации. Объясните их содержание.
| № п/п | Сумма денежной выручки, у.е. | Стоимость основных производственных фондоф, тыс. у.е. | Оборотные фонды, тыс. у.е. | Численность работников, чел.
| Площадь сельхоз- угодий, га | Энерге- тические мощности, л.с. | Покупка кормов, ц | Услуги сельхоз- химии, тыс. у.е. | Услуги агропром-техники, тыс. у.е. |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 1310 | 1544 | 288 | 38 | 510 | 480 | 25 | - | - |
| 2 | 1262 | 1562 | 322 | 37 | 430 | 410 | 30 | - | 6 |
| 3 | 1092 | 498 | 304 | 36 | 354 | 342 | 30 | - | 6 |
| 4 | 1074 | 536 | 330 | 30 | 350 | 340 | 35 | 5 | - |
| 5 | 1144 | 586 | 354 | 28 | 390 | 370 | 20 | 5 | - |
| 6 | 1206 | 464 | 318 | 32 | 414 | 390 | 15 | 4 | 5 |
| 7 | 1302 | 626 | 370 | 40 | 510 | 400 | - | 6 | 5 |
| 8 | 1414 | 608 | 340 | 42 | 520 | 426 | - | 8 | 5 |
| 9 | 1546 | 646 | 388 | 40 | 530 | 430 | - | 10 | - |
| 10 | 1506 | 644 | 374 | 44 | 532 | 440 | 15 | 15 | - |
| 11 | 1454 | 716 | 410 | 43 | 520 | 410 | 20 | 14 | 4 |
| 12 | 1522 | 704 | 424 | 37 | 560 | 504 | - | 13 | 4 |
| 13 | 1636 | 674 | 390 | 42 | 606 | 640 | - | 10 | - |
| 14 | 1644 | 652 | 396 | 41 | 610 | 710 | 30 | 8 | - |
| 15 | 1686 | 598 | 384 | 44 | 620 | 678 | - | 5 | 5 |
| 16 | 1614 | 570 | 348 | 45 | 630 | 540 | 15 | 10 | 5 |
| 17 | 1636 | 516 | 306 | 50 | 636 | 550 | 25 | 10 | 6 |
| 18 | 1574 | 474 | 290 | 60 | 600 | 614 | 20 | 15 | 6 |
| 19 | 1546 | 458 | 286 | 55 | 570 | 600 | 10 | 5 | 8 |
| 20 | 1484 | 424 | 310 | 54 | 554 | 410 | 10 | 4 | 8 |
| 21 | 976 | 406 | 272 | 33 | 320 | 374 | 30 | 4 | - |
| ИТОГО | 29628 | 13906 | 7204 | 871 | 10766 | 10058 | 330 | 151 | 73 |
| Ср. арифм. отклон | 1410,86 | 662,19 | 343,1 | 41,5 | 512,7 | 478,9 | 15,7 | 7,2 | 3,5 |
| Ср. квадр. откл. | 294,5 | 302,2 | 45,2 | 8,0 | 96,3 | 110,7 | 8,4 | 3,7 | 1,9 |
| Vx, % | 20,9 | 45,6 | 13,2 | 19,3 | 18,8 | 23,1 | 53,5 | 51,4 | 54,3 |
1. Среднее арифметическое отклонение рассчитываем по формуле:
![]() ,
,
где Х – значение варианта показателя; n – число хозяйств или опытов.
Например:
Х = 29628\21=1410,86 и т.д.
Значения средних арифметических отклонений представлены в таблице.
2. Среднее квадратическое отклонение рассчитываем по формуле:
σ2x = ∑(xi - x¯)2\n
σ2x = (1310-1410,86)2 +(1262-1410,86)2 +(1092-1410,86)2 +(1074-1410,86)2 +(1144-1410,86)2 +(1206-1410,86)2 +(1302-1410,86)2 +(1414-1410,86)2 +
(1546-1410,86)2 +(1506-1410,86)2 +(1454-1410,86)2 +(1522-1410,86)2 +
(1636-1410,86)2 +(1644-1410,86)2 +(1686-1410,86)2 +(1614-1410,86)2 +
(1636-1410,86)2 +(1574-1410,86)2 +(1546-1410,86)2 +(1484-1410,86)2 +
(976-1410,86)2 \21 = 86711,3
σx = 294,5
Таким образом, сумма денежной выручки в среднем отклоняется в сторону увеличения средней арифметической и в сторону ее уменьшения на 294,5 тыс. у. е.
σ2x = (1544-662,19)2 + (1562-662,19)2 +(498-662,19)2 +(536-662,19)2 +
+ (586-662,19)2 +(464-662,19)2 +(626-662,19)2 +(608-662,19)2 +
+(646-662,19)2 +(644-662,19)2 +(716-662,19)2 +(704-662,19)2 +
+(674-662,19)2 +(652-662,19)2 +(598-662,19)2 +(570-662,19)2 +
+(516-662,19)2 +(474-662,19)2 +(458-662,19)2 +(424-662,19)2 +
+(406-662,19)2 /21=91352,7
σx = 302,2
Стоимость основных производственных фондов в среднем отклоняется в сторону увеличения средней арифметической и в сторону ее уменьшения на 302,2 тыс. у. е.
σ2x = (288343,1)2 +(-322-343,1)2 +(304-343,1)2 +(330-343,1)2 +(354-343,1)2 +(318-343,1)2 +(370-343,1)2 +(340-343,1)2 +(388-343,1)2 +(374-343,1)2 + (410-343,1)2 +(424-343,1)2 +(390-343,1)2 +(396-343,1)2 +(384-343,1)2 + (348-343,1)2 +(306-343,1)2 +(290-343,1)2 +(286-343,1)2 +(310-343,1)2 + (272-343,1)2 /21 = 2045,6
σx = 45,2
Оборотные фонды в среднем отклоняется в сторону увеличения средней арифметической и в сторону ее уменьшения на 45,2 тыс. у. е.
σ2x = (38-41,5)2 + (37-41,5)2 + (36-41,5)2 + (30-41,5)2 + (28-41,5)2 + (32-41,5)2 + (40-41,5)2 + (42-41,5)2 + (40-41,5)2 + (44-41,5)2 + (43-41,5)2 + (37-41,5)2 + (42-41,5)2 + (41-41,5)2 + (44-41,5)2 + (45-41,5)2 + (50-41,5)2 + (60-41,5)2 + (55-41,5)2 + (54-41,5)2 + (33-41,5)2 /21= 64,05
σx = 8,0
Численность работников в среднем отклоняется в сторону увеличения средней арифметической и в сторону ее уменьшения на 8,0 чел.
σ2x = (510-512,7)2 +(430-512,7)2 +(354-512,7)2 +(350-512,7)2 +(390-512,7)2 +(414-512,7)2 +(510-512,7)2 +(520-512,7)2 +(530-512,7)2 +(532-512,7)2 + (520-512,7)2 +(560-512,7)2 +(606-512,7)2 +(610-512,7)2 +(620-512,7)2 + (630-512,7)2 +(636-512,7)2 +(600-512,7)2 +(570-512,7)2 +(554-512,7)2 + (320-512,7)2 /21= 9272,12
σx = 96,3
Площадь сельхозугодий в среднем отклоняется в сторону увеличения средней арифметической и в сторону ее уменьшения на 96,3 га.
σ2x = (480-478,9)2 +(410-478,9)2 +(342-478,9)2 +(340-478,9)2 +(370-478,9)2 + (390-478,9)2 +(400-478,9)2 +(426-478,9)2 +(430-478,9)2 +(440-478,9)2 + (410-478,9)2 +(504-478,9)2 +(640-478,9)2 +(710-478,9)2 +(678-478,9)2 + (540-478,9)2 +(550-478,9)2 +(614-478,9)2 +(600-478,9)2 +(410-478,9)2 + (374-478,9)2 /21=12252,81
σx = 110,7
Энергетические мощности в среднем отклоняется в сторону увеличения средней арифметической и в сторону ее уменьшения на 110,7 л.с.
σ2x = (25-15,7)2 +(30-15,7)2 +(30-15,7)2 +(35-15,7)2 +(20-15,7)2 +(15-15,7)2 + (15-15,7)2 +(20-15,7)2 +(30-15,7)2 +(15-15,7)2 +(25-15,7)2 +(20-15,7)2 + (10-15,7)2 +(10-15,7)2 +(30-15,7)2 /21= 70,7
σx = 8,4
Покупка кормов в среднем отклоняется в сторону увеличения средней арифметической и в сторону ее уменьшения на 8,4 ц.
σ2x = (5-7,2)2 +(5-7,2)2 +(4-7,2)2 +(6-7,2)2 +(8-7,2)2 +(10-7,2)2 +(15-7,2)2 +(14-7,2)2 +(13-7,2)2 +(10-7,2)2 +(8-7,2)2 +(5-7,2)2 +(10-7,2)2 +(10-7,2)2 +(15-7,2)2 +(5-7,2)2 +(4-7,2)2 +(4-7,2)2 /21=13,6
σx = 3,7
Услуги сельхозхимии в среднем отклоняется в сторону увеличения средней арифметической и в сторону ее уменьшения на 3,7 тыс. у.е.
σ2x = (6-3,5)2 +(6-3,5)2 +(5-3,5)2 +(5-3,5)2 +(5-3,5)2 +(4-3,5)2 +(4-3,5)2 +(5-3,5)2 + (5-3,5)2 +(6-3,5)2 +(6-3,5)2 +(8-3,5)2 +(8-3,5)2 /21=3,7
σx = 1,9
Услуги агропромтехники в среднем отклоняются в сторону увеличения средней арифметической и в сторону ее уменьшения на 1,9 тыс. у.е.
3. Коэффициент вариации Vx , отражает среднюю колеблемость показателя и рассчитывается по формуле:
Vx = (σx\ х) ·100.
В нашем случае Vx = (294,5\1410,86)·100 = 20,9%.
Vx = (302,2\662,19)·100 = 45,6%.
Vx = (45,2\343,1)·100 = 13,2%.
Vx = (8,0\41,5)·100 = 19,3%.
Vx = (96,3\512,7)·100 = 18,8%.
Vx = (110,7\478,9)·100 = 23,1%.
Vx = (8,4\15,7)·100 = 53,5%.
Vx = (3,7\7,2)·100 = 51,4%.
Vx = (1,9\3,5)·100 = 54,3%.
Задание 3
На основе приведенных ниже данных рассчитайте индивидуальные и общие индексы.
| Количественные и качественные показатели производства продукции | |||||||
| № п/п | Виды продукции | Количество, ц | Цена за 1 ц, у.е. | Индивидуальные индексы | |||
| V0 базисный период | V1 текущий год | C0 базисный период | C1 текущий год | Физического объема | Цен | ||
| 1 | Овощи | 502 | 546 | 128 | 152 | 1,09 | 1,19 |
| 2 | Фрукты | 696 | 686 | 112 | 123 | 0,99 | 1,10 |
| 3 | Молоко | 206 | 172 | 218 | 209 | 0,83 | 0,96 |
| 4 | Говядина | 298 | 282 | 142 | 158 | 0,95 | 1,11 |
1. Индивидуальные индексы рассчитываем по формулам:
In =W1 /W0 ,
где W1 ,W0 -- значение показателя соответственно в отчетном и базисном году.
Соответственно: In =V1 /V0 , In =C1 /C0 ,
In овощи = 546/502=1,09 , In овощи = 152/128=1,19 ,
In фрукты = 686/696=0,99, In фрукты = 123/112=1,10 ,
In молоко = 172/206=0,83, In молоко = 209/218=0,96,
In говядина = 282/298=1,11, In говядина = 158/142=1,11 .
2. Общие индексы стоимости всей продукции вычисляем по формуле :
Ic= ∑V1C1/ ∑V0C0
Ic=∑ V1C1/ ∑V0C0 = 546*152+686*123+172*209+282*158 / 502*128+696*112+206*218+298*142= 247874/229432=1,080 или 108 %.
Индекс показывает, что стоимость всей продукции увеличилась в отчетном периоде по сравнению с базисным, на 8%.
Общий индекс физического объема продукции вычисляем по формуле:
Iv= ∑V1C0/ ∑V0C0
Iv= ∑V1C0/ ∑V0C0 = 546*128+686*112+172*218+282*142 / 502*128+696*112+206*218+298*142= 224260/229432= 0,977 или 97,7%
Индекс показывает, что объем производства продукции в отчетном периоде по сравнению с базисным снизился на 2,3%.
Список литературы
1. Громыко Г.Л. Статистика. – М.: Изд-во МГУ им. Ломоносова, 1981.
2. Гусарев В.М. Теория статистики. – М.: ЮНИТИ, 1998.
3. Елисеева И.И., Юзбашев. Общая теория статистики: учеб. для вузов. – М.: Финансы и статистика, 1995.
4. Ефимов М.Р., Петров Е.В., Румянцев В.Н. Общая теория статистики: Учебник для вузов. – М.: Инфра-М, 1996.
5. Национальное счетоводство: учебник для вузов / Под ред. Г.Д.Кулагиной. – М.: Финансы и статистика, 1997.
6. Общая теория статистики: Статистическая методология в коммерческой деятельности: учебник для вузов / Под ред. А.С. Спирина и О.Е.Башиной. – М.: Финансы и статистика, 1994.
7. Социальная статистика: учебник для вузов / Под ред. И.И.Елисеевой. – М.: Финансы и статистика, 1997.
8. Статистика: Курс лекций для вузов / Под ред. В.Г.Ионина. – М.: ИНФРА-М, 1996.
9. Экономическая статистика: Учебник / Под ред. Ю.Н.Иванова. – М.: ИНФРА-М, 1998.
10. Статистика. Раздел 1 "Общая теория статистики и математическая статистика". Курс лекций. / Сост.: Мизина Е.В. – Донецк: ДонГТУ, 2001.
Похожие работы
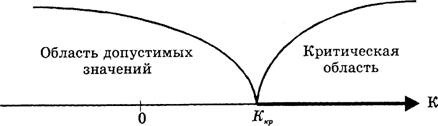
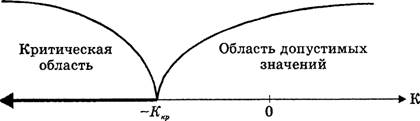
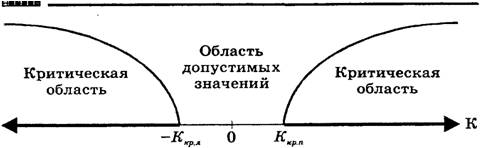
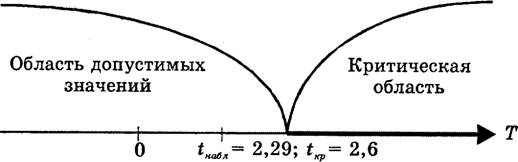
... ошибки первого рода; 3) определить область допустимых значений и так называемую критическую область; 4) принять то или иное решение на основе сравнения фактического и критического значений критерия. Проверка статистических гипотез складывается из следующих этапов: - формулируется в виде статистической гипотезы задача исследования; - выбирается статистическая характеристика гипотезы; - ...
... критических точек распределения ([1], стр. 465), по уровню значимости =0,05 и числу степеней свободы 8-3=5 находим Т.к. , экспериментальные данные не противоречат гипотезе и о нормальном распределении случайной величины . Для случайной величины : Используя предполагаемый закон распределения, вычислим теоретические частоты по формуле , где - объем выборки, - шаг (разность между ...
... mx , соответствующий доверительной вероятности b. Действительно, так как то Пользуясь таблицей значений интеграла по значению b найдем величину а следовательно, и сам доверительный интервал le = 2. Проверка статистических гипотез Принятие решения о параметрах генеральной совокупности играет исключительно важную роль на практике. Рассмотрим вопрос о принятии решения на примере ...
... вида выборочного наблюдения; 6) установление сроков проведения наблюдения; 7) определение потребности в кадрах для проведения выборочного наблюдения, их подготовка; 8) оценка точности и достоверности данных выборки, определение порядка их распространения на генеральную совокупность. Представление о статистических данных, как о выборочных, может относиться не только к собственно выборке, но и ...

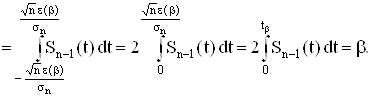
0 комментариев