Сызықтық программалаудың негізгі есептері

1.1 Сызықтық программалау есептері.

Қәзіргі кездегі ғылымдардың даму ерекшеліктерінің бірі-олардың әртүрлі салаларын зерттеуде математикалық әдістер мен есептеуіш техникаларының кеңінен қолданылуында. Егер бұдан бұрынғы уақыттырда математикалық амалдар мен әдістер тек астрономия, физика, химия ғылымдарында қолданылып келсе, соңғы кезде бұл ғылыми жетістіктер медицина, лингвистика және экономика ғылымының көптеген процестері мен құбылыстарын зерттеуде ұтымды пайдаланып жүр. Мұның өзі ақиқатты танып білуде әртүрлі ғылымдар саласында диалектикалық бірліктің күшейіп және теориялық көзқарастың тереңдей түсуінен деуге болады.

Соңғы жылдар бедерінде халық шаруашылығын тиімді басқаруда математикалық әдістер мен есептеуіш техникалары жиі қолданылуда. Осының негізінде еліміздің экономикасын жоспарлы түрде дамытып, еңбек тиімділігін арттырудың жаңа мүмкіндіктері пайда болды. Осы ретте қол жеткен мүмкіндіктерді қысқаша ғана атап айтсақ, олар: экономиканың даму жоспары; шаруашылықты басқару шешімдерінің нақтылығы мен дәлелділігінің артуы; жоспарді іс жүзінде асыру барысында жасалынатын бақылау процестеріне ерекше жылдамдық беру, т.б.

Адамзат қоғамы дами бастауынан үнемділік, тиімділік деген мәселелер бірге жасасып келеді. Үнемділік, тиімділіктің математикалық түбірі функциялардың экстремум мәндерімен тығыз байланысты. Экономикалық есептердің алғашқы үлгісі гректерде кездеседі. Ұзындығы белгілі l доғамен шектеуге болатын ең үлкен ауданды табу керек. Ең үлкен және ең кіші мәндерді табу есептері экономикалық мәселелерде жиі кездеседі. Мұндай экономикалық есептерді экономикалық-математикалық мделдеу пәні қарастырады.

Экономикалық-математикалық моделдеу математикада қарастырылатын экстремалдық есептер курсының бөлімі болып табылады. Экономикалық есептер үш топқа бөлініп қарастырылады: сызықтық программалау есептері, сызықтық емес программалау есептері және динамикалық программалау есептері.

Бұл көптен бері құлаш жайып, дамып келе жатқан ғылым. Бұл салада алғашқылардың бірі совет экономисті А.Н.Толстой (1930ж) еңбектері. Венгер математигі Б.Эгервари (1931ж) “таңдау проблемасы” есебінің математикалық қойылымын қарастырып, сызықтық программалау есебінің шешімін тапқан. Бұл есепті шешу әдісі осы ғалым құрметіне венгер әдісі деп аталады. Совет ғалымдары Л.В.Канторович, В.С.Немчинов, В.В.Новожилов, А.Л.Луръе және т.б. математиктер мен экономистердің жұмыстарында сызықтық және сызықтық емес программалаудың математикалық теориясы экономикалық проблемаларды зерттеудің әдістері ретінде дамып отырды. Бұл салада тек совет ғалымдары емес сонымен қатар басқа елдер ғалымдарының да атқарған қызметі мол. Солардың ішінде америка ғалымы Хичкок (1941ж) транспорт есебінің берілуін қойды, Данциг (1949ж) сызықтық программалау есебін шығарудың симплекс әдісін жасады. Сызықтық және сызықтық емес программалау есептерінің шығару әдістері Форд, Фалкерсон, Кун, Ламке, Гасс, Чарнес, Бил еңбектерінде берілді. Толық зерттелген есептер сызықтық программалау есептері. Динамикалық программалау есептері үлкен қарқынмен өрістеп келеді.

Өндірістік процестерді зерттеуде кеңінен қолданылатын тәсілдердің бірі-сызықтық программалау. Сызықтық программалау дегеніміз өндірістің негізгі мақсаты мен шарты белгілі бір сызықтық өрнектер (теңдеулер) түрінде берілген жағдайда, сол процесті зерттеу үшін қолданылатын математикалық тәсіл. Математика тілімен айтқанда, сызықтық программалау дегеніміз белгісіздеріне сызықтық теңсіздіктер түрінде шарт қойылған, сызықтық функцияның ең үлкен немесе ең кіші мәндерін табатын ғылым.

Сызықтық программалау есептерінің жалпы түрі былай жазылады.

Берілген

(1.1.1)

мақсат функциясына минимал мән әперетін және мына теңсіздіктерді:

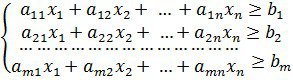(1.1.2)

(1.1.3) қанағаттандыратын

векторын табу.

Бұл жердегі берілген тұрақты сандар, оның үстіне m < n

Жоғарыда келтірілген мысалдарға сәйкес, (1.1.2), (1.1.3) теңсіздіктерін есептің шектеуіш шарты деп, ал (1.1.1)сызықтық формасын есептің мақсат функциясы деп атайды.

Сызықтық программалау есептерінде барлық деп жорамалдауға болады, өйткені олардың ішінде теріс сандар кездесетін болса, онда сәйкес теңдеуді (-I) көбейту арқылы ді оң санға айналдыруға болады.

Жеке мысалдарда есептің негізгі (1.1.2) щарты бірнеше түрде берілуі мүмкін. Мысалы, есептің негізгі теңсіздіктері тек қана түрінде немесе түрінде жазылуы мүмкін. Сол себептен,есептің негізгі теңсіздіктерініңформасына қарай сызықтық программалау есептерін бірнеше түрге бөлуге болады.

Егер сызықты программалау есептері мына түрде берілсе:

(1.1.4)

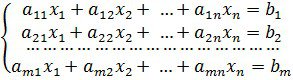(1.1.5)

(1.1.6)

онда бұндай мысалды сызықтық программалау есебінің канон түрі деп атайды.

Егер сызықтық программалау есептері мына түрде берілсе:

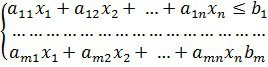
онда мұндай мысалды сызықтық программалау есебінің стандартты түрі деп атайды.

Сызықтық программалау мысалдары әр түрде берілгенімен, олар бір-біріне эквивалентті, өйткені, канон түрінде берілген есеп стандартты түрде оңай түрленеді, немесе керісінше, стандартты түрде берілген есеп канон түріне оңай келтіріледі. Енді осы жағдайларды қарастыралық. Мысалы сызықтық программалау есебінің негізгі шарты мына түрде берілсін:

Онда осы теңсіздікке белгісізін қосу арқылы оны теңдікке айналдырамыз, яғни

осы теңсіздікті теңдеуге айналдырушы белгісізін есептің қосымша белгісізі деп атайды.

Енді есептің негізгі шарты теңдеу түрінде берілсін:

онда осы теңдеуді екі теңсіздіктер түрінде жазуға болады, яғни

соңғы теңсіздіктердің екіншісін (-I) көбейтіп, кез-келген теңдеудің төмендегі екі теңсіздіктер түрінде жазылатынын көреміз:

сонымен есебіміз канон түрінде берілсе, онда оның әрбір теңдеуіне екі теңсіздікті сәйкес қою арқылы стандартты түрге көшіруге болатынын, ал стандартты түрден канон түріне қосымша белгісіздер ендіру арқылы көшіруге болатынын көрдік. Осы тұрғыда ескерте кететін тағы бір жағдай, ол пен тің эквивалент екендігінде.

Енді сызықтық программалау есептерін бір түрден екінші түрге көшіруге мысал қарастыралық.

Берілген мысалды сызықтық программалаудың канон түріне келтір.

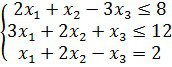
Қосымша және белгісіздерін бірінші және екінші теңсіздіктердің оң жағына қосып жазып, мынадай канон есебін аламыз:

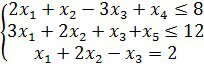
Егер сызықтық программалау есебінің негізгі шарты (1.1.5) теңдеулер системасы түрінде беріліп, ал белгісіздерінің кейбіреулері үшін (1.1.6) теңсіздігі орындалмайтын болса, онда ол мысал канон түріндегі есепке жатпайды. Осындай есептерді толық канон түріне келтіру үшін оның барлық белгісіздері (1.1.3) шартын қанағаттандыратындай жағдай жасау қажет.

1.2 Сызықтық программалаудың негізгі теоремалары.

Сызықтық программалаудың негізін құрайтын теоремалармен танысайық:

1-теорема. Сызықтық программалау есебінің шешімдерінің жиыны – дөңес.

Дәлелдеу. Сызықтық программалау есебінің шешімінің сызықтық комбинациясы да сол есептің шешімі болатынын дәлелдеу қажет. Ол үшін векторлары сызықтық программалау есебінің шешімдері делік. Олай болса

,

және

,

Енді осы жоспарлардың кез-келген сызықтық комбинациясын қарастыралық:

,

Осы жоспардың есептің шешімі болатынын көрсетелік. Ол үшін мына амалдарды орындаймыз.

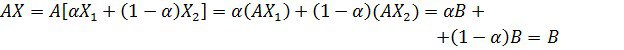
бұдан AX=Bекендігі шығады.

Жорамалымыз бойынша

болғандықтан . Демек теорема дәлелденді.

2-теорема.Сызықтық программалау есебінің мақсат функциясы өзінің оптимал шешімін дөңес көпжақтың шеткі нүктесінде қабылдайды. Егер сызықтық функция өзінің оптимал шешімін бірнеше шеткі нүктеде қабылдаса, онда сол нүктелердің дөңес сызықтық комбинациясы да есептің оптимал шешімі болады.

Дәлелдеу. Теореманың шарты бойынша сызықтық программалау есебінің анықталу облысын төбелерінің саны шекті көпжақ құрайды. Жазықтықта көпжақтың көпбұрыш болатыны белгілі. Теореманың дәлелдеуін жазықтықта қарастыралық. Көпбұрышты Д – деп, ал оның шет нүктелерін деп белгілейік. Есептің оптимал шешімі болсын (сурет 1). Олай болса кез-келген X үшін болады.

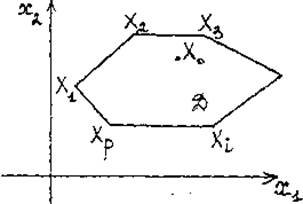
сурет 1

Егер шеткі нүкте болса, онда теорема дәлелденеді. Енді ішкі нүкте болған жағдайды қарастыралық. Онда ол нүкте көпбұрыштың бұрыш нүктелерінің (шет нүктелері) сызықтық комбинация арқылы өрнектеледі, яғни

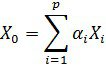
бұл жердегі

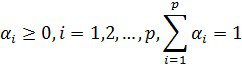
бізде сызықтық функционал болған себепті:

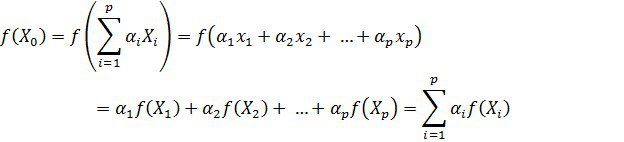
Барлық ішіндегі ең кішісін тауып, оны m-ге тең делік. Ал барлық ішіндегі ең кіші мәні үшін орындалсын делік. Демек

Енді соңғы өрнектегі барлық - ді ге ауыстырсақ, онда мынадай теңсіздік аламыз:

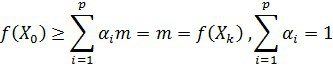
яғни

Теореманің шарты бойынша оптимал жоспар. Ал соңғы теңсіздік көпбұрыштың шеткі нүктесінде басқа оптимал шешім болатынын көрсетеді. Бұл қарама-қайшылық дің шет нүкте екенін дәлелдейді.

Енді осы теореманың екінші жартысын дәлелдейік. Ол үшін функциясы бірнеше нүктеде минимал мән қабылдайды делік. Ол нүктелерді біз деп белгілейік. Демек

Енді Xнүктесі осы нүктелердің дөңес сызықтық комбинациясы делік, яғни

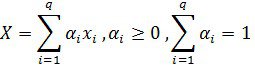
функционалдың осы нүктедегі мәнін қарастырамыз:

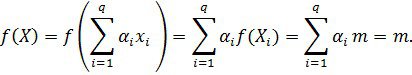
Бұдан нүктелерінің дөңес сызықтық комбинациясының да есептің минимал мәнін беретінін көрдік. Теорема дәлелденді.

3-теорема. Егер k(k=n) өзара тәуелсіз векторлар системасы берілген болып, олар үшін теңдігі барлық тар үшін орындалса, онда векторы есептің анықталу облысын беретін көпжақтың шеткі нүктесі болады.

Дәлелдеу. нүктесі анықталу облысының ішкі нүктесі деп жорамалдайық. Олай болса ол нүкте сол облыстың екі шеткі нүктелерінің сызықтық комбинациясы түрінде бейнеленеді, яғни

Берілген векторының n-k компоненті нөлге тең болғандықтан, ал векторларының компоненттерінің теріс болуы мүмкін емес екенін және 0<<1 екенін ескерсек, онда векторларының да n-k компоненттері нөлге тең болады. Демек

Жорамалдауымыз бойынша осы екі нүкте есептің анықталу облысында жатыр. Демек олар үйлесімді жоспарлар. Олар үшін мынадай теңдіктер:

орындалады. Осы теңдіктерді векторлар түрінде жазсақ, онда:

осы екі теңдеудің айырымы:

теореманың шарты бойынша векторлар системасы сызықтық тәуелсіз. Демек соңғы теңдік тек қана

болғанда орындалады.

Бұдан

екені шығады. Басқа сөзбен айтқанда, X нүктесін екі шеткі нүктенің сызықтық комбинациясы түрінде бейнелеуге болатынын аламыз. Бұрыш нүктесінің (шет нүктенің) анықтамасын еске түсірсек, онда X нүктесінің шет нүкте екенін аламыз. Сонымен теорема дәлелденді.

4-теорема. Егер шеткі нүкте болса, онда барлық оң

болатын терге сәйкес келетін векторлар өзара сызықтық тәуелсіз.

Дәлелдеу. X векторының алғашқы компоненті нөлге тең емес делік. Олай болса алғашқы векторлары үшін

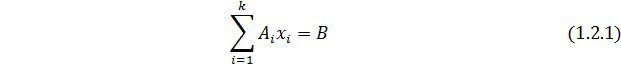
Осы теңдікті қанағаттандыратын векторлар системасы өзара сызықтық тәуелді делік. Олай болса, бәрі бірдей нөлге тең емес сандары табылып олар үшін

(1.2.2)

теңдігі орындалады. Теореманың шарты бойынша

Кез-келген санын алып, оны (1.2.2) теңдеуіне көбейтеміз деодан шыққан қорытындыны теңдеуіне бірінші, қосу, сосын алу нәтижесінде мынадай теңдеулер аламыз:

Соңғы теңдеулер системасы теңдеуінің екі шешімі бар екенін және олардың

тең екенін көрсетеді. Бұл жерде барлық болғандықтан ді және векторларының барлық компоненттері оң болатындай етіп таңдап алуға болады. Бұл жағдайда мен жоспар болады, ал

Демек X векторы басқа екі нүктенің сызықты комбинациясы түрінде бейнеленіп отыр. Бұл жағдай теореманың шартында айтылған, X шеткі нүкте деген шартқа қайшы келеді. Демек X шеткі нүкте (бұрыш нүктесі).

1.3 Сызықтық программалау есептерін шешудің графиктік әдісі.

Графиктік әдіс сызықтық программалау есебінің геометриялық мағынасына негізделіп, көбіне екі өлшемді кеңістік есептерін және үш өлшемді кеңістіктің кейбір есептерін шешуде қолданылады, себебі жартылай кеңістіктердің қиылысынан тұратын шешімдер көпжағын құрудың жеткілікті ауыртпалығы бар. Үштен жоғары өлшемді кеңістік есебін геометриялық түрде кескіндеу мүмкін емес.

Сызықтық программалау есебі екі өлшемді кеңістікте берілсін, яғни шектеулері екі айнымалыдан болсын

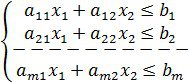(1.3.2)

(1.3.3)

Жүйе (1.3.2), (1.3.3) үйлесімді, шешімдер көпбұрышы шектеулі делік. Әрбір теңсіздік (1.3.2), (1.3.3) жарты жазықтықты шеттік түзулерімен , , бірге анықтайды. Сызықтық функция (1.3.1) Z=h мәніндегі түзулерді береді; . Шектеулер жүйесінің шешімдер көпбұрышын (1.3.2) және сызықтық функцияның (1.3.1) Z=0 мәніндеі графигін тұрғызайық. Онда қойылған сызықтық программалау есебіне мынадай геометриялық мағына беріледі. тірек түзуі және мұнда функция Z min мәнін қабылдайтын шешімдер көпбұрышының нүктесін табу керек.

мәндері N = () векторы бағытында өсетіндіктен, Z=0 түзуін N бағытында өзіне-өзін параллель жылжытамыз.

Сурет 1-ден шешімдер көпбұрышының екі тірек түзуі (А және С нүктелерінде) болатындығын, әрі min мәні қабылданатын нүктесінің координаталарын АB және AE түзулерінің теңдеулер жүйесін шешу арқылы табу керектігін көреміз.

Егер шешімдер көпбұрышы шекеусіз облыс болса, екі жағдай мүмкін.

1 – жағдай. түзуі N векторы бағытында немесе оған қарама-қарсы бағытта қозғала отырып шешімдер көпбұрышын кесіп отырады және бірде-бір нүктесінде оған тірек болмайды. Бұл жағдайда сызықтық функция шешімдер көпбұрышында жоғарыдан да, төменнен де шектеусіз (сурет 2).

2 – жағдай. Түзу қозғала отырып, шешімдер көпбұрышына тірек болады (сурет 3). Онда облыс түріне байланысты сызықтық функция жоғарыдан шектеулі және төменнен шектеусіз (сурет За), төменнен шектеулі және жоғарыдан шектеусіз (сурет 3б) немесе жоғарыдан да, төменнен де шектеулі (сурет 3в) болуы мүмкін.

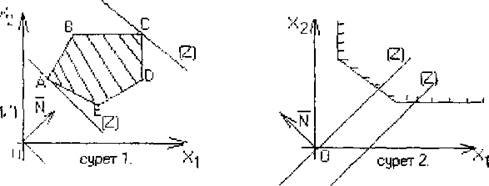
сурет 3

Мысалдар.

1. Шикізатты пайдалану есебі.

Екі түрлі , Р₂ өнім шығару үшін үш түрлі шикізат қолданылады. Шикізат қорлары, әрбір өнімнің бір өлшемі үшін жұмсалатын әрбір шикізат шамасы және өнімнің бір өлшемін өткізуден түсетін пайда шамасы кестеде көрсетілген. Өнімді max пайда алатындай етіп, ұйымдастыру қажет.

Шикізат түрлері	Шикізат Қоры	Өнім өлшемін жасауға жұмсалатын шикізат мөлшері
	6	1	1
	10	3	1
	20	2	5
Өнім өлшемінен түсетін пайда		10	8

Шешуі. -ден , Р₂ -ден х₂ мөлшерінде өнімдер дайындалсын. Өнімнің бір өлшем шамасын дайындауда жұмсалатын шикізаттар мөлшерін жөне олардың қорларын: ескерсек келесі шектеулер жүйесін аламыз

Теңсіздіктер жұмсалатын шикізаттар қордағы барынан аспайтындығын көрсетеді.

Есептің мақсаты, өнімдерді өткізуден түсетін max пайданы, екі айнымалының және х₂ функциясы деп қарастырамыз. P₁ өнімінің х₁ мөлшері өткізгенде 10х₁, Р₂ өнімінің х₂ мөлшері өткізгенде 8х₂, барлығы, қосындыда Z=10x₁+8x₂ (теңге) пайда келтіреді. Сонымен, шектеулер жүйесінің

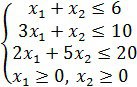
сызықтық функция Z=10x₁+8x₂max мәнін қабылдайтын нақты шешімдерін табу керек. Шешімдер көпбұрышын шекаралық түзулер арқылы

,

тұрғызамыз. Ол үшін кезкелген нүктені, мысалы координаталар бас нүктесін алып, теңсіздік қай жарты жазықтықты беретінін анықтаймыз. Теңсіздік жарты жазықтығын белгілеу арқылы, шешімдер көпбұрышын ОАВС құрамыз.

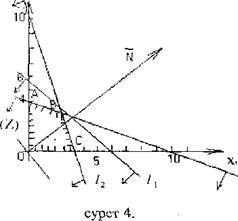
N = (10; 8) = 2(5; 4) векторын және (Z) түзуін тұрғызамыз. (Z) түзуін өзіне-өзін параллель N векторы бағытында жылжыта отырып, шешімдер көпбұрышының В нүктесінде тірек түзуіне айналып, бұл нүктеде функция Z_max мәнін қабылдайтынын көреміз.

В нүктесі және түзулердің қиылысында жатқандықтан, оньң координаталарын тендеулер жүйесін

шешіп табамыз . Есептің оптималдық шеімі , Z_max.

Сонымен 47,69т. көлеміндегі пайда келтіру үшін мөлшерінде , мөлшерінде Р₂ өнімдерін шығаруды жоспарлау тиімді.

2.Рацион құру есебі.

Бордақылауда әрбір жануар күніне ең кемінде 10 өлшем S₁, 8 өлшем S₂ және 10 өлшем S₃ қоректік заттарын қабылдауы тиіс. Рацион екі түрлі жемнен құрылады. Әрбір жемнің килограмындағы қоректік заттардың мөлшері және жемдердің бағалары кестеде берілген.

Қажетті қоректік заттары жеткілікті және жалпы шығын min-ды болатын күндік рацион құру керек.

Есептің математикалық моделін құрайық.

Қоректік заттар	1 кг жем қүрамындағы қоректік зат мөлшері
	жем I	жем II
S1	2	1
S2	1	1
S3	1	4
Жем кг-ның бағасы	3	4

Күндік рациондағы жемдер тиісінше х₁ және х₂ кг десек, кестедегі цифрлар арқылы қоректілік сақталу үшін

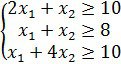
теңсіздіктерінің орындалуы қажетті. Егер жем рационда қолданылмаса х₁ 0 немссе х₂ 0 болады, кері жағдайда немесе . Жалпы жағдайда, , шарттары орынды.

Есептің мақсаты күндік рационға min шығын жұмсау болғандықтан, рацион құнын сызықтық функциясы арқылы анықтап, осы функцияның min мәнін табу талап етіледі. Есеп көп шешімді, х₁ және х₂ шексіз көп мәндер қабылдауы мүмкін. Сонымен, теңсіздіктер жүйесінің

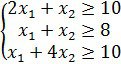
сызықтық функцияға мәнін беретін шешімдерін табу керек.

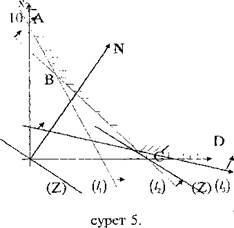
Шешуі. О координаталар жүйесінде шекаралық түзулерді

,

,

,

және осы түзулерге қарағанда теңсіздіктер анықтайтын жарты жазықтықтар қиылысында шешімдер көпбұрышын тұрғызамыз. Нәтижесінде A,B,C,D бұрыштық нүктелері (төбелері) болатын, шектеусіз көпбұрышты облысты аламыз. N(3,4) векторын және (Z) түзуін тұрғызып, Z түзуін өзіне-өзін параллель N векторы бағытында жылжыта отырып, шешімдер көпбұрышының С нүктесінде алғаш тірек түзуіне айналатынын көреміз (сурет 5). Түзуді әрі қарай жылжыта берсек, сызықтық функцияның мәні шешімдер көпбұрышының нүктелерінде өсе бастайды. Демек С нүктесінде сызықтық функция min мәнін қабылдайды. Бұл нүкте түзулердің қиылысында жатқандықтан

теңдеулер жүйесін шешу арқылы координаталарын , табамыз. Табылған мәндерді сызықтық функцияға қойсақ, аламыз.

Сонымен min шығын жұмсау үшін күндік рационды кг I – жемнен, II – жемнен құру қажет.

Жалпы графиктік әдіспен n-m=2 болатын сызықтық программалау есебін шеше аламыз. Мұндағы n – айнымалылар (белгісіздер) саны, m – сызықтық тәуелсіз тендеулер саны.

Сызықтық программалау есебін қарастырайық.

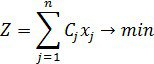
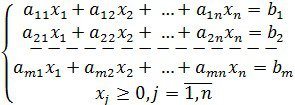
Бұндағы барлық теңдеулер сызықтық тәуелсіз және n-m=2 ұатынасы орындалсын.

Жордан – Гаусс әдісімен m жою барсында алғашқы m айнымалылар x₁, x₂, … , x_m – базистік, ал соңғы екі айнымалы x_m+1, x_n – еркін айнымалыларға айналсын делік, яғни жоғарыда көрсетілген шектеулер мына түрге келтірілсін

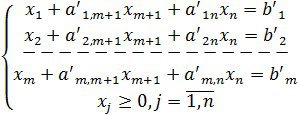(1.3.4)

Түрленген жүйе (1.3.4) теңдеулері арқылы сызықтық функцияны тек еркін айнымалылармен өрнектейміз де, базистік айнымалыларды шығарып тастап, теңсіздіктермен берілген шектеулерге көшеміз. Ақырында келесі есепті аламыз.

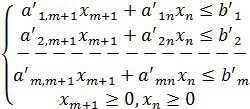
бұл есепте екі айнымалы ғана болғандықтан графиктік әдіспен шеше аламыз. Оптималдық х_m+1 және х_n мәндерін тауып, (1.3.4)-ге қою арқылы, x₁,x₂,...,x_m оптималдық мәндерін табамыз.

1.4 Сызықтық программалау есебін шешудің симплекс әдісі.

Сызықтық программалау есебінің оптималдық шешімі тірек шешімдерінің ішінен іздестіріледі, әрбір тірек шешімі берілген n векторлар жүйесіндегі m сызықтық тәуелсіз вектролармен анықталғандықтан, олардың саны терулерінің санынан аспайды.

m және n сандары жеткілікті үлкен болғанда оптималдық шешімді барлық тірек шешімдерін құру арқылы іздестру өте қиын.

Симплекс әдісі белгілі тірек шешімінен келесі жақсартылған трек шешіміне көшіріп отырады, санаулы қадымнан соң оптималдық шешімге келтіріледі; есептің шешімі жоқ немесе сызықтық функциясы шектеусіз болса, оны да көрсетеді.

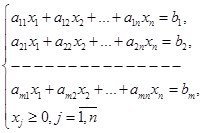
есебін қарастырайық және мұндағы , болсын.

Шектеулер жүйесінің алғашқы m векторлары бірлік векторлар балсын делік. Онда есеп мына түрде қойылады

(1.4.1)

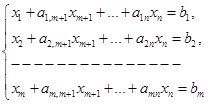(1.4.2)

(1.4.3)

Теңдеулер жүйесін (1.4.2) векторлық түрде жазайық

(1.4.4)

мұндағы

, , … , , , … , ,

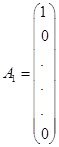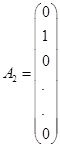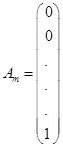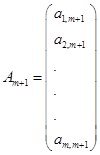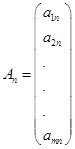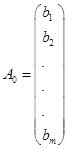
m-өлшемді кеңістіктің сызықтық тәуелсіз векторлары осы кеңістіктің базисін жасайтындықтан, (1.4.4) жіктелуіндегі айнымалыларын базистік деп, еркін айнымалыларын нөлге теңестірп, болғандықтан алғашқы

(1.4.5)

шешімін аламыз. Осы шешімге сәйкес

(1.4.6)

жіктелуіндегі векторлары сызықтық тәуелсіз, демек құрылған алғашқы шешім есептің тірек шешімін береді.

Бастапқы тірек шешімнен (1.4.5) келесі тірек шешімді қалай құратындығын қарастырайық. m-өлшемді кеңістіктің (1.4.4) өрнектегі әрбір векторы базистік векторлары арқылы бір ғана түрде былай жіктеледі

,

Базиске енбеген, мысалы векторының,

(1.4.7)

әйтеуір бір коэфифициенті оң таңбалы болсын делік. Әзірге белгісіз шамасына (1.4.7) теңдікті көбейтіп, (1.4.6) теңдіктен шегерсек,

(1.4.8) теңдігін аламыз. Сонымен

Векторының компоненттері теріс таңбалы болмаса, шешімді береді. болғандықтан, - векторының теріс таңбалы -лер енетін компоненттері теріс таңбалы бола алмайды. Сондықтан кезкелген үшін

(1.4.9) болатындай мәнін табу қажет. (1.4.9) теңсіздіктен

демек

, (1.4.10)

шартын орындайтын кезкелген үшін векторы есептің шешімін береді.

Тірек шешмінің m+1 оң таңбалы компоненті болмайтындықтан, шешімінің , , компоненттерінің кемінде біреуін нөлге айналдыру қажет. (1.4.10) теңсіздіктегі мәнін алсақ шешімінің min қабылдайтын компоненті нөлге айналады. Бұл компонент бірінші орындағы, яғни болсын делік. мәнін (1.4.8)-ге қойып

жіктелуін аламыз, бұл жаңа тірек шешімі

сәйкес. Мұндағы

,

арқылы базистен векторды шығарып, орнына жаңа вектор енгізуді бізде Жордан – Гаусс әдісімен бір базистен екінші базиске көшу болғандықтан, векторлар жүйесі сызықты тәуелсіз және жаңа базисті береді. Жаңа тірек шешімді құру базиске енгізілетін векторды таңдаудан және базистен шығарылатын векторды анықтаудан тұрады. Симплекс әдісінің негізгі элементтерінің бірі базиске енгізілетін векторды анықтау белгісі. Егер базиске енгізілетін вектор ретінде анықталып, оның жіктелуіндегі (1.4.7) барлық

болса, онда (1.4.8) жіктелуінен бір векторды шығаратындай таңдау мүмкін емес. Бұл жағдайда шешімі m+1 оң таңбалы компонентті, ал

вектролар жүйесі сызықты тәуелді болып, шешімдер көпжағының сызықтық функция min мәнін қабылдай алмайтын, бұрыштық емес, ішкі нүктесін анықтайды. Сондай-ақ, бұл, сызықтық функция гипержазықтығы векторына қарама-қарсы бағыттағы қандай қашықтықта болса да шешімдер көпжағына тірек жазықтық бола алмайтынын, яғни сызықтық функция шешімдер көпжағында шектеусіз екендігін көрсетеді.

Сонымен сызықтық программалау есебінің бос мүшелері теріс таңбалы емес шектеулер жүйесі құрамында бірлік базис болса, онда қосымша есептеулерсіз-ақ алғашқы тірек шешімін, сондай-ақ векторлардың базиске жіктелу коэффициенттерін алуға болады.

Мысал.

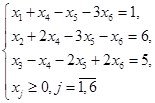
Тірек шешімін құрып, жаңа тірек шешіміне көшу керек.

Шешуі. Теңдеулер жүйесін векторлық түрде жазсақ

ЕСЕП ЖАЗ

Енді симплекс әдісінің оптималдық шешімін табу және оcы әдістің оптималдық шарттарын құрайық.

,

,

есебінің шешімдері бар және әрбір тірек шешімі ұүнарлы делік. Онда

тірек шешіміне

(1.4.11)

(1.4.12)

,

ал кезкелген векторына берілген базисінде

(1.4.13)

(1.4.14)

теңдіктері тиесілі.

Сызықтық функцияның векторына сәйкес коэффициентін деп белгілейміз. Онда келесі теорема орындалады.

Теорема 1. Егер әйтеуір бір векторына шарты (белгісі) орындалса, онда шешімі оптималды емес және теңсіздігі орындалатын Х шешімін құруға болады.

Дәлелдеуі. (1.4.13) және (1.4.14) теңдіктерін -ға көбейтіп, (1.4.11) және (1.4.12) теңдіктерінен шегереміз

, (1.4.15)

(1.4.16)

Теңдіктің екі жағына да қосылған. Бұл теңдіктердегі , , сондықтан - лер түгелімен дерлік оң таңбалы болатындай - ны табуға болады. Демек, есептің жаңа шешімін

және оған (1.4.16)- шы өрнек бойынша тиісті сызықтық функцияның

мәнін аламыз. Теорема шартында және , онда

.

Салдар. Егер әйтеуір бір шешім -дің базисінде барлық , векторларының жіктеулеріне

(1.4.17)

шарты (белгісі) орындалса, онда шешім - оптималды.

Сызықтық функцияның min мәнін табу есептің оптималдық шарты (белгісі) (1.4.17) теңсіздіктерімен анықталады, ал мәндері шешім бағалары деп аталады.

Сонымен, сызықтық функция min –мын табу есебінің шешімі оптималды болуы үшін оның бағаларының оң таңбалы болмауы қажетті және жеткілікті.

Сызықтық программалаудың сызықтық функция max –мын мәнін табу есебі үшін келесі теорема орынды.

Теорема 2. Егер әйтеуір бір векторына шарты (белгісі) орындалса, онда шешімі оптималды емес және болатын Х шешімін құруға болады.

Дәлелдеуі. Теорема 1 –дегідей.

Салдар. Егер әйтеуір бір шешім -дің базисінде барлық , векторларының жіктеулеріне

(1.4.18)

Шарты (белгісі) орындалса, онда шешім оптималды.

(1.4.18) теңсіздіктері сызықтық функцияның max мәнін табу есебінің оптималдық шарты (белгісі).

Сонымен, сызықтық функция max –мын табу есебінің шешімі оптималды болуы үшін оның бағаларының теріс таңбалы болмауы қажетті және жеткілікті.

д

Сызықтық программалаудың транспорт есебі транспорт пен өнеркәсіп және өндірістің түрлі мәселелерінің теориялық зерттеулерінде және практикада жиі қолданылады. Әсіресе өнеркәсіп пен ауылшаруашылық өнімдерін жеткізуді рационализациялауда, сондай – ақ жүк айналымдарын оптималды жоспарлауда және транспорттың басқа да әртүрлі жұмыстарында ерекше маңызы бар. Барлығы m ұсынушыда, -де , ,жинақталған біртекті заттарды, барлығы n тұтынушыға, -де , жеткізу керек. Бірлік жүкті і - ұсынушыдан j-тұтынушыға тасымалдау бағасы белгілі.

Тұтынушылар сұранысын толық қанағаттандыратын және бағасы минималды болатын, барлық жүкті тасымалдау жоспарын құру қажет.і - ұсынушыдан j-тұтынушыға тасымалдауға жоспарланған жүкті деп белгілеп, есептің шартын жоспарлау матрицасы аталатын кестемен жазуға болады.

Ұсынушылар	Тұтынушылар				Қорлар
A1	x11		…
А2	c21 x21	c22 х22	…	c2n x2n
...	…	…	…	…	…
Ат	cm1 xm1	cm2 xm2	…	cmn xmn
Сұраныстар			…

Есептің математикалық моделін құрайық .

i-ұсынушыдан j-тұтынушыға тасымалданатын жүк x_ij, оның тасымал бағасы C_ijx_ij. Барлық жүкті тасымалдау бағасы

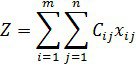
Шектеулер жүйесін есептің келесі шарттарынан аламыз:

1) Барлық жүк тасымалдануы керек, яғни

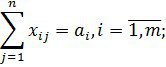
(бұл теңдеулер кестенің жолдарынан алынады).

2) Сұраныстар түгелімен қанағаттандырылуы керек, яғни

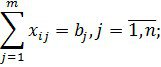
(бұл теңдеулер кестенің бағандарынан алынады).

Сонымен, транспорт есебінің математикалық моделі келесі түрде беріледі.

Сызықтық функцияның

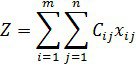
ең кіші мәнін келесі шектеулерде

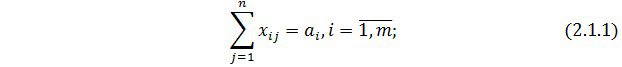
табу керек.

Қарастырып отырған моделде қорлар қосындысы сұраныстар қосындысына тең деп есептелінеді.

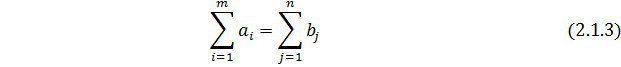
Бұндай модель тұйықталған (жабық) деп аталады.

Теорема.

Қорларының қосындысы сұраныстарының қосындысына тең болатын кез-келген транспорт есебінің шешімі бар.

Теореманы дәлелдеу үшін, берілген шарттарда кемінде бір шешімі бар екендігін және сызықтық функция шешімдер жиынында шектеулі екендігін көрсету қажет.

Дәлелдеуі.

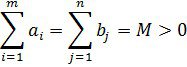
делік , онда:

шамалары (2.1.1), (2.1.2) шектеулер жүйелерін қанағаттандыратындықтан, есептің шешімі болады. Шындығында да, мәндерін (2.1.1) және (2.1.2)-ке қойсақ, табамыз

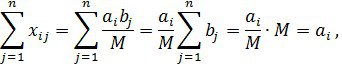
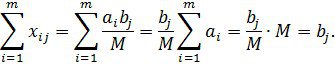
мәнін алып, сызықтық функцияны бағаласақ, (2.1.2) теңдік арқылы мынаны аламыз

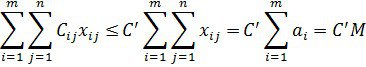
Дәл сол сияқты мәнін қолдансақ

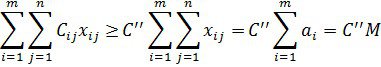
Соңғы екі теңсіздікті біріктіріп қарастырсақ теңсіздігін аламыз, яғни сызықтық функция транспорт есебі шешімдерінің жиынында шектеулі.

2.2 Алғашқы таяныш жоспарын құру әдісі.

Оптималдық шешімге бастапқы тірек шешімін құрумен жуықтайды.

Шектеулер жүйесінің (2.1.1)-(2.1.2) m, n белгісіздері, m+n тендеулерімен берілген, сондай-ақ (2.1.3) қатынаспен байланысты.

Жүйенің (2.1.1) және (2.1.2) бөліктерінің теңдеулерін өз алдыларына қосса, бірдей екі тендеу алынады. Бұл жүйенің сызықты тәуелділігін көрсетеді, егер біреуін шығарып тастасақ, онда шектеулер жүйесінің m + n – l сызықты тәуелсіз теңдеулері қалады. Сонымен, транспорт есебінің құнарлы тірек шешімінің m + n – l оң таңбалы компоненті немесе тасымалы бар, яғни (), матрицасының m + n – l элементі ғана оң таңбалы да, қалғандары нөлге тең.

Транспорт есебінің шарты және тірек шешімі кестеде жазылса үлес бөлінген клетка бос емес, үлес бөлінбегені бос клетка деп аталады. Құнарлы тірек шешімінде m + n – l бос емес клетка базистік айнымалыларға тән. Шектеулер (2.1.1), (2.1.2) түрінде жазылса, тірек шешіміне енген базистік айнымалыларға сызықты тәуелсіз векторлар жүйесі тән. Транспорт есебі кесте түрінде жазылса, үлестірулер тірек шешімін береді, егер ациклды болса, яғни төбелері бос емес клеткалардан тұйық цикл құруға болмаса.

Бір бағанда немесе бір жолда көрші екі клеткасы ғана орналасатын, сондай-ақ соңғы клеткасы бірінші клеткасымен бір жолда немесе бір бағанда жататын клеткалар жиынтығы цикл деп аталады.

Циклды құру кезкелген бос емес клеткадан басталады. Бағанмен (жолмен) келесі бос емес клеткаға, одан тік бұрылып жолмен (бағанмен) келесі бос емес клеткаға, тағы сол сияқты көшулермен бастапқы клеткаға оралуға тырысады. Қайта оралу мүмкін болса цикл алынғаны, үлестіру тірек шешімі емес. Тік бұрылатын клеткалар циклдың төбелерін анықтайды. Кері жағдайда үлестіру тірек шешімі болады.

Транспорт есебінің бос емес клеткалары m + n – l – ден артық кез-келген үлестіруі тірек шешімі бола алмайды, себебі оған сызықты тәуелді векторлар жүйесі тән. Бұндай үлестіруде, кестеде, кез келген уақытта бос емес клеткалар санын m + n – l -ге дейін кемітуге көмектесетін тұйық цикл құруға болады.

Құнарлы тірек шешімді анықтайтын, яғни ациклды бос емес клеткаларға әйтеуір бір бос клетканы тіркесек, тірек шешім болмай қалады да, бір төбесінен басқалары түгелдей бос емес клеткаларға жататын, жалғыз цикл пайда болады.

Транспорт есебінің бастапқы тірек шешімін сызықтық программалау есебінің осыған дейінгі әдістері мен құруға болады, бірақ бұл үлкен есептеулерді керек етеді. Бастапқы тірек шешімін құрудың бірнеше жеңіл жолдары бар, соларды мысалдар арқылы қарастырамыз.

Солтүстік-батыс бұрыш әдісі.

Жүк бірінші тұтынушыға сұранысы орындалғанша түгелдей бірінші ұсынушыдан, жетпегені екіншісінен, ол да жетпесе үшіншісінен, т.с.с., жасалады.

Егер бірінші ұсынушының қоры сұраныстан артық болса, қалғаны екінші тұтынушыға, одан қалғаны үшіншіге, т.с.с., барлық қоры біткенше тасымалданады.

Қалған тұтынушылар мен ұсынушылар арасындағы тасымал да осы тізбекпен жалғасады. Тасымалдау тізбегі транспорт есебі кестесінің солтүстік-батыс бұрышынан басталып, оңтүстік-шығыс бұрышында аяқталады.

Мысал.

Келесі есептің математикалық моделін және бастапқы тірек шешімін құру керек.

Ұсынушылар	Тұтынушылар				Қорлар
	2	4	7	9	200
	5	1	8	12	270
	11	6	4	3	130
Сұраныстар	120	80	240	160	600

Шешуі. – – ұсынушыдан – тұтынушыға тасымал көлемі болсын. Барлық жүкті тасымалдау бағасы

болатындай келесі шектеулер жүйесінің шешуін табу керек

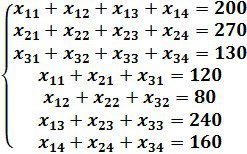
Ұсынушылар	Тұтынушылар				Қорлар
	2 120	4 80	7	9	200
	5	1	8 240	12 30	270
	11	6	4	3 130	130
Сұраныстар	120	80	240	160	600

Бірінші ұсынушының қоры = 200 тұтынушының сұранысы = 120, клеткасына 120 тасымалданып, бағаннің басқа клеткалары сызылады, қалдық екінші тұтынушыға тасылады. Екінші тұтынушы сұранысы қалдығымен жабылады, сонымен клеткасына 80 тасымалданып, бағанының қалған клеткалары сызылады. Үшінші тұтынушының сұранысы екінші ұсынушының қорынан кем, сұраныс түгелімен орындалып, бағанының қалған клеткалары сызылады, қалдық келесі сұраушыға өтеді. Төртінші тұтынушының сұранысы үшінші ұсынушының қоры және қалдығымен орындалады.

Құрылған тасымалдың жалпы құнының үлестері бар клеткалардың бұрыштарындағы сандар көбейтінділерінің қосындысынан аламыз:

Осы тасымал жоспарының есептің тірек шешімі екндігіне көз жеткізейік. Бос емес клеткаларды бағандар және жолдармен байланыстырып, тұйық цикл, яғни кез келген бос емес клеткадан бастап қозғалып, осы клеткаға оралатын бос емес клеткалар тізбегін құру мүмкін емес. Ол түгілі клеткасынан баған бойымен келесі бос емес клеткаға да бара алмаймыз. Демек, бұл тасымал тірек шешімін, бос емес клеткалар саны m + n – l = 6 санынан кем болғандықтан құнарсыз тірек шешімін береді. Бос емес клеткалар саны 5.

Бұл үлестіру тасымалдау бағалары ескерілмей орындалғандықтан оптималды шешімнен алшақ болуы мүмкін. Осы бағалар ескерілетін кейбір әдістерді қарастырайық.

Бұндай әдістердің бірі кіші құн әдісі болып табылады.

Кестедегі ең кіші құн жазылған () клеткасына сандарының кішісі жазылып, қоры түгелдей тасылған ұсынушы жолы, немесе сұранысы түгелденген тұтынушы бағаны, немесе болса жол да, баған да сызылады.

Кестенің қалған бөлігінен тағы да кіші құн клеткасы таңдалып, жоғарыдағыдай әрекет қайталанады. Осылайша үлестіру барлық қорлар тасымалданып, сұраныстар түгелімен орындалғанша жалғасады.

Осы әдіспен бұған дейінгі есептің шешуін табайық. Есеп шартын кестеге жазып, барлық әрекетті орындасақ

циклқұрумүмкінемесүлестіруіналамыз. Мұндағыm + n – l саныүлестірулерсанынатең, яғниқұнарлытірекшешіміалынғаны.

Ұсынушылар	Тұтынушылар				Қорлар
	2 120	4	7 80	9	200
	5	1 80	8 30	12 160	270
	11	6	4 130	3	130
Сұраныстар	120	80	240	160	600

Тасымалдың жалпы құны

Солтүстік-батыс бұрыш әдісімен алынған сандағыдан артық, оптималдық шешімнен алшақтай түскен.

Әрбір бағанның ең кіші құн орналасқан клеткаларына V белгісі қойылып, дәл осылай белгілеу әрбір жолдың клеткаларына да қайталанады. Нәтижесінде қос VV белгісі бар клеткалар шығады. Тасымалдау әуелі қос VVбелгілі клеткаларға, әрі қарай кіші құн әдісімен жасалады. Ұсынушы қоры түгесілсе-жол, тұтынушы сұранысы орындалса-баған сызылып отырады. Бұндай әдіс қос мүмкіндік әдісі болып табылады.

Жоғарыда келтірілген есепті қос мүмкіндік әдісімен де қарастырайық.

Ұсынушылар		Тұтынушылар			Қорлар
	VV 2 120	4	7 80	9	200
	5	VV 1 80	8 160	12 30	270
	11	6	V 4	VV 3 130	130
Сұраныстар	120	80	240	160	600

Алдымен клеткаларын толтырамыз. клеткасы түгесілген қорға байланысты жолымен бірге сызылады. Кестенің қалған бөлігін кіші құн әдісімен толтырамыз: . Тасымалдау нәтижесінде

Құнарлы тірек шешімін алдық. Оның құны

Қарастырылған әдістерімен есептің құнарлы немесе құнарсыз тірек шешімдерін құрамыз. Шешімді оптималдыққа дейін симплекс әдісімен жеткізуге болады. Бірақ транспорт есебінің симплекс кестесі айнымалы, улкен болғандықтан және көп есептеуді қажет еткендіктен көбіне қарапайым әдістерді қолданады. Жиі қолданылатын потенциалдар әдісін қарастырайық.

2.3 Потенциялдар әдісі.

Теорема – 1.

Транспорт есебінің шешуі оптималды болса, онда оған

, егер және

, егер

Шарттарын қанағаттандыратын, барлығы m + n және сандарының жүйесі сәйкес. Сандар және тиісінше ұсынушылар және тұтынушылар потенциалдары деп атайды.

Дәлелдеуі.

,

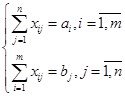
Транспорт есебін сызықық программалаудың қайсыбір бастапқы есебіне қосалқы деп қарастырсақ, онда бастапқы есеп

түрінде беріледі.

- қосалқы есептің оптималды шешуі, сондықтан

бастапқы есептің шешуі, қосалқылық теоремасына сәйкес немесе

.

Белгілі теоремаға сүйенсек, қосалқы есептің оптималды шешуінің оң таңбалы компоненттеріне сәйкес бастапқы есеп шектеулері қатаң түрде теңдеулер түрінде, ал нөлдік компоненттеріне сәйкес шектеулері теңсіздіктер түрінде өрнектеледі, яғни

Сонымен, бастапқы тірек шешімі оптималды болу үшін, келесі шарттардың орындалуы қажетті:

а) үлесті клетка үшін потенциалдар қосындысы тасымалдау бағасына тең, яғни

( * )

б) үлессіз клетка үшін потенциалдар қосындысы тасымалдау бағасынан аспауы қажет, яғни

( ** )

Кемінде бір үлессіз клетка үшін (**) шарты орындалса, шешім оптималды емес, осы клеткаға тиісті векторды базиске енгізу, яғни клеткаға үлес бөлу арқылы шешімді жақсарта түсуге болады.

Потенциялдар жүйесін құрып, шешімді оптималдылыққа тексереді. Әдіс алгоритімын мысалмен қарастырайық. Транспорт есебінің кестесіне потенциялдар жазылатын бір жол және бір баған қосылады.

Потенциалдар жүйесін құрып көрейік.

Құнарлы тірек шешімінің бос емес (үлесті) клеткаларына белгісіздерінің саны m+n сызықты тәуелсіз m+n – 1 теңдеулер жүйесі

( * )

құрылады. Теңдеулерінің саны белгісіздерінен біреуі кем бұл анықталмаған жүйенің бір белгісізіне, әдетте - ге нөл мәнін беріп, қалған потенциалдарды бір мәнді етіп анықтайды.

потенциалы белгілі десек, онда ;

егер потенциалы белгіліболса, онда .

Сонымен, белгісіз потенциал үлесті клетканың шамасынан белгілі потенциалды шегерумен табылады.

Кесте 1

		Тұтынушылар
Ұсынушылар		=2	=4	=11	=15	Қорлар
	=0	2 120	4 - 80	7 4	9 + 6	200
	=-3	5	1 + 0	8 240	12 - 30	270
	=-12	11	6	4	3 130	130
Сұраныстар		120	80	240	160

Кесте 1 – де тірек шешімі құнарсыз, бір үлесті клетка жетіспейді (m+n-1=6, үлес саны 5 ). Сондықтан, үлесті клеткаларының саны ең көп жолды,

немесе жолын таңдаймыз да, =0 ( немесе =0) деп аламыз. =0 мәніне байланысты мәндері табылады:

жолы, бағандары арқылыбасқа потенциалдарды табу мүмкін емес. Бұл үзіліс бастапқы тірек шешімінің құнарсыздығынан. Құнарсыздықты нөлді үлестіріп жоюға болады. Нөл бөлінетін клеткалар жалған үлесті деп аталады.

Жалған үлесті клетканы жолдарының әйтеуір бір бос клеткасына нөлді бөліп, ендірміз. Сызықтық функцияны минимизмциялау есебі қарастырылып отырғандықтан, жалған үлесті етіп, тасымал құны ең кіші клетканы алу тиімді.

жолдарындағы бос клеткалардың орналасқан клеткасына нөлді жазып, үлесті етеміз. Бұл клетка потенциалын потенциалымен, клеткасы потенциалын потенциалымен, клеткасы потенциалын потенциалымен, клеткасы потенциалын потенциалымен байланыстырады.

Потенциалдар жүйесі құрылды. Әрбір үлесті клеткада

( * )

шарты орындалса, жүйенің дұрыстығы; кері жағдайда жүйені қайта құру немесе ( * ) шарты орындалатындай етіп өзгерту керек.

Бос емес ( үлессіз ) клеткаларда оптималдық шартының орындалуын тексеру:

Жолдардың әрбір үлессіз клеткасында ( ** ) шартының орындалуын тексереміз, яғни қиылысында бос клетка жататын жол мен баған потенциалдарын қосып, осы клеткадағы тасымалдау құнымен салыстырамыз.

Барлық үлессіз клеткаларда теңсіздігі орындалса, шешім оптимады. Егер кейбір клеткаларда болса, онда шешім оптималды емес, бұндай клеткаларда айырымын сол жақ төменгі бөлігіне шығарып жазамыз.

Кесте 1 – де үлессіз клеткаларды аламыз:

жолында :

жолында ;

жолында

, клеткаларында отималдық шарты орындалмайды, айырымдарды клетканың сол жақ төменгі бөліктеріне жазып қоямыз.

Сызықтық программалаудың транспорт есебі сызықты функцияның min мәнін табуды талап еткендіктен оның алгоритмі де min есебінің симплекс әдісінің жалпы принципімен орындалады.

Үлесті клеткаларды базистік векторларға балап, үлессіздерін-қалған векторларға баласақ, сызықтық программалаудың жалпы есебінде базиске мәніне сәйкес келетін вектор енгізетіндіктен, транспорт есебінде мәні потенциалдар қосындысына баланып, үлес жіберілетін клетка ретінде мәніне сәйкес клетка таңдалады. Қарастырылып отырған мысалда мәні тиісті клеткасын үлесті ету қажет. Ол үшін қанша жүк үлесі бөлінетіндігін алдынала анықтаймыз.

Цикл құру және айналымдық жүкті анықтау.

Үлесті ету қажет клетканы “+” таңбасымен белгілеп, бос емес клеткалар қатарына қосамыз. Енді кестедегі үлесті клеткалар саны m+n болғандықтан, бір төбесінен басқа төбелері түгел үлесті клеткалардан тұратын цикл құрылады. Циклды тауып “+” таңбалы клеткасынан кейінгі төбелерін кезекпен “–” және “+” таңбаларымен белгілеп шығамыз да, мәнін анықтаймыз. Мұндағы -лер циклдың “–” белгілі төбелеріндегі үлестер, - цикл бойынша айналымға түсетін үлес шамасын анықтайды. Енді - мәнін “+” таңбасымен белгіленген үлесті ету қажет клеткасына жазамыз да, цикл бойымен жылжи “+” белгілі клеткалар үлестеріне қосып, “–” белгілі клеткалар үлестерінен шегеріп шығамыз. Егер - бірнеше минималды үлеске тән болса, шегеруден шыққан нөлдік үлестерді жаңадан алынған тірек шешімінің бос емес ( үлесті ) клеткаларының саны m+n – 1 болатындай етіп қалдырамыз.

Үлесті ету клеткасы “+” таңбасымен белгіленіп, кесте 1- де пунктирмен көрсетілген цикл құрылады да, анықталып, цикл бойымен тиісті өзгерістер енгізіледі.

Кесте 2

		Тұтынушылар
Ұсынушылар		2	4	11	- 15 9	Қорлар
	0!	2 120	4 - 50	7 + 4	9 30	200
	-3	5	1 + 30	8 - 240	12	270
	+ 12 -6	11	6	4 1	3 130	130
Сұраныстар		120	80	240	160

-ді айналымға түсіріп, жаңа тірек шешімі, кесте 2 алынды, бұл шешімде оптималдыққа тексеріледі. Потенциалдар жүйесін қайтадан құрып, әрбір бос клеткада оптималдық шартының орындалуын тексеруге болады.

Алынған шешім оптималды бомаса 4-кезеңдегі әрекеттер қайталанады. Процесс барлық бос клеткаларда (**) шарты орындалғанша жалғасады

,, мәндерін, сондай-ақ “+” , “–” таңбаларын қаламмен жазып, өшіріп отыру арқылы оптималды шешімді бір ғана кестені пайдалана отырып іздестіруге болады.

Жаңа потенциалдар жүйесін құрып, оптималдыққа бос клеткаларды тексеріп отыру едәуір уақытты қажет еткендіктен, есептеу жұмыстарын біршама жеңілдетерлік потенциалдар жүйесін өзгерту әдісін қарастырамыз.

Потенциадар жүйесін өзгерту:

Жаңа тірек шешімінде (клетка 2) бұрынғы потенциалдар жазылған, үлесті клеткасында, шарты орындалмайды, . Сондықтан не - ді, не - ті алтыға шегеруіміз қажет. Нәтижесінде азғана потенциалдар өзгеретін потенциал кемітіледі. потенциалын кемітіп, - ді қарастырсақ бір ғана потенциалы өзгереді. Кері жағдайда барлық потенцилдар өзгерілер еді. Потенциал - ді “!” белгісімен, - ті “–”, пен байланысты - ті “+” бнлгісімен таңбалап, өзгерістер енгізілетін тізбекті құрамыз. Осы тізбектегі “–” таңбалы потенциалды кемітеміз, “+” таңбалы потенциалды өсіреміз, “!” таңбалы потенциалды өзгеріссіз қалдырамыз. Сонда барлық бос емес клеткаларда (*) шарты орындалады.

Потенциал кемітілгендіктен бұл бағандағы бос клеткаларда оптималдық шарты орындалмауы мүмкін емес. Оптималдық шарты орындалмайтын бос клеткалар потенциалы өсірілген жолда (бағанда) ғана пайда болуы мүмкін. Потенциал алтыға өсірілді, жолының бос клеткаларын оптиамалдыққа тексереміз: -4<11; -2<6; 5>4.

Клетка бұл шартты қанағаттандырмайды. Сондай-ақ бұл шарт клеткасында орындалмағанлықтан айырымдарын сол жақ төменгі бұрыштарына жазамыз.

келесі үлесті ету клеткасын анықтайды, бұл клеткаға “+” белгісін қойып, циклды құрып, төбелерін “–” және “+” белгілерімен алма–кезек таңбалап, мәнін табамыз. Цикл бойымен мәнін айналымға түсіріп, клеткасының үлесіне 50-ді бөлу арқылы жаңа тірек шешімін (кесте 3) аламыз.

Соңғы жуықтау арқылы шешім 200-ге жақсара түсті. Бұл клеткасындағы айырымын, осы клеткаға бөлінген үлестің 50 көбейтіндісінен анықталды.

		Тұтынушылар				Қорлар
Ұсынушылар		2	- 4 0	- -11 7	9
	0!	2 120	4	7 50	9 30	200
	+ -3 1	5	1 80	8 190	12	270
	-6	11	6	4	3 130	130
Сұраныстар		120	80	240	160

Соңғы алынған кесте 3 тірек шешімінде потенциалдар жүйесін өзгертіп, оптималдыққа тексереміз. Құрылған потенциалдар жүйесі алынған шешімнің оптималды екендігін көрсетеді. Тасымалдау құны 2850.

Ескерту. Цикл өзін-өзі қиып өтетін де болуы мүмкін.