Навигация
ОСНОВЫ ПРОЕКТИРОВАНИЯ НА ПЛИС
Омский государственный технический университет
А.П.Аверченко, В.Г.Шахов
ОСНОВЫ ПРОЕКТИРОВАНИЯ НА ПЛИС
Учебное пособие
Омск, 2016
УДК 004.083
Рецензенты: д.т.н., профессор В.И.Потапов,
д.т.н., профессор В.П.Горелов
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
В настоящее время программируемые логические интегральные схемы (ПЛИС) являются одним из перспективных направлений развития современной микроэлектроники. Это объясняется следующими факторами.
1. Микропроцессорные техника и технологии привели к направлению развития вычислительной техники и ее приложений, включая мультимедийные приложения, IP - технологии, Интернет и связанные с ними достижения в области связи и дистанционных взаимодействий. В этой области не столь существенны производительность, помехоустойчивость и безотказность работы оборудования. Здесь же по-другому решаются вопросы информационной безопасности и защиты информации, поскольку при использовании ПЛИС отпадают проблемы с дистанционными и групповыми атаками, что является бичом IP- технологий.
2. ПЛИС могут использоваться при тиражировании современных технических средств различного уровня, от бытовой техники до современных технических средств оперативного управления и контроля. Они могут обладать следующими положительными свойствами:
- независимость от импортных программных продуктов зарубежного производства, включая Windows, Apple, Cisco и прочие программно ориентированные корпорации, что позволяет защититься от внешних нежелательных воздействий и финансовых проблем, связанных с лицензированием и обновлениями программных продуктов;
- ограничения технического шпионажа или дистанционных нежелательных воздействий на оборудование и технологически процессы;
- новые возможности оперативного перепрограммирования, включая дополнительную защиту от внешних атак и модернизацию алгоритмов работы оборудования.
3. Разработка, изготовление и тиражирование ПЛИС являются новым толчком современных нанотехнологий и основой для развития техники будущего. При разработке и тиражировании ПЛИС используются последние достижения в области физики, математики, химии и их практических приложений.
4. Разрабатываются новые приемы программирования и альтернативных операционных систем. Они могут включаться в новые системы автоматизированного проектирования (САПР) и способствуют созданию новых систем программирования и проектирования, включая блочное и объектно - ориентированное программирование. Удобством такого подхода является то, что любой автор собственной системы программирования является независимым владельцем и правообладателем своей системы программирования, предназначенной для решения узкого круга задач. Это не исключает создания тиражируемых систем программирования, которые могут являться объектами интеллектуальной собственности, следовательно, являются объектом коммерциализации.
5. Инженер - разработчик, имеющий в своем арсенале современные ПЛИС, обладающие огромными ресурсами по производительности, объему памяти и возможностями конфигурирования, получает существенные преимущества для создания, модернизации и тиражирования современных систем автоматизации, управления и комплексирования в множестве прикладных задач современных цифровых технологий.
1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПЛИС
В этот раздел входят основные сведения из следующих направлений технической кибернетики:
- булева алгебра и исчисление высказываний;
- теория конечных автоматов;
- конечные динамические системы и машины Тьюринга;
- обучающиеся системы и искусственный интеллект.
Множество задач, входящих в эти разделы, слишком объемно, но авторы надеются, что означенные направления послужат толчком для дальнейшего самообразования и послужат основой для дальнейшего поиска в сети Интернет. Помните, что для корректной работы в любом направлении нужно умение корректно ставить задачи: на 70 – 80% это обеспечивает решение задачи. В ссылочных материалах приводятся некоторые данные об Интернет – ссылках по рассматриваемым проблемам.
1.1. Основы булевой алгебры и ее приложений
Несмотря на то, что основы этого направления были заложены еще в Древней Греции, принято считать, что его основоположником являлся Джордж Буль, преподаватель одного из колледжей Великобритании. В основе его теории лежала алгебра множеств, в то время уже достаточно разработанная, поэтому булева алгебра может считаться одним из ответвлений алгебры множеств.
В основе булевой алгебры лежит понятие двоичного аргумента - переменной, которая может принимать одно из двух значений: ноль или единица (0 или 1). В терминах Древней Греции это ассоциируется с понятиями «истина» (true) или «ложь» (false), что и было основой для раздела философии под названием «логика».
С исторической точки зрения, интерес к этому направлению появился во второй половине ХХ века при изобретении первых компьютеров. В их основе лежали электромагнитные реле, состоящие из катушки с сердечником и подвижным якорем, к которому механически присоединены контактные группы. При подаче напряжения на обмотку якорь притягивается к сердечнику, и при этом часть контактов или размыкается, или замыкается. Это послужило основой для развития современной цифровой техники.Использование принципа двоичной логики послужило толчком для современной цивилизации. Не исключено, что впоследствии будет переход на так называемую нечеткую логику, более приближенную к деятельности живых организмов. Тем не менее, алгоритмы нечеткой логики можно моделировать и на ПЛИС.
Булева функция оперирует с конечным множеством из каргументов. При этом, если каждый из аргументов принимает одно из двух значений, 0 или 1, возникает область определения, состоящая из конечного числа точек. Их количество оценивается как 2К, где К – количество аргументов.Обычно эту область называют пространством определения, а в булевой алгебре ассоциируют его с к– мерным кубом. В нем вершины определяют область определения, ребра имеют единичную длину, а координаты являются двоичными кодами этих вершин. При этом 0 – мерный куб представляет собой единственную точку с координатой 0, 1 – мерный куб – это отрезок единичной длины с координатами (0,1), двумерный куб – это квадрат с четырьмя координатами , трехмерный - это обычный куб в смысле Эвклида и т.д. Кубы большей мерности наглядно не воспринимаются (хотя алгоритм изображения кубов мерности 4 и выше можно записать в виде простого правила: для представления куба мерности к + 1 достаточно изобразить два к – мерных куба и соединить соответствующие вершины одномерными ребрами. Попробуйте изобразить эти кубы: после этого вы поймете технологии 4D).
ВариантыК- мерных кубов приведены на рис. 1.1.Здесь варианты а, б,в,г соответствуют нуль - одно - двух и трехмерным вариантам кубов.
Рисунок 1.1. - Варианты К - мерных кубов
Четырехмерный вариант куба не показан (хотя он освоен в технологиях типа 4D и их преемников). Остальные вариации пока считаются абстракцией, но это пока!
Вариантов задания булевых функций может быть несколько. Основными среди них можно считать табличный, алгебраический и графо - аналитический.
При табличном методе строится двумерная таблица, включающая столбцы с вариантами значений аргументов, столбцы с вариантами функций и строки со вариантами значений полученных функций.
Приведем таблицу булевых функций одного аргумента. Всего таких функций может быть 4. Их описание и функции приведены на рис.1.2. Как видно из рисунка, всего функций одного аргумента четыре. Из них две вырожденные и являются константами. Первая константа - 0: она сохраняет свое значение независимо от значения аргумента. Вторая константа, константа 1, сохраняет свое значение, но с другим знаком. Это второстепенные функции, не представляющие интереса для математики.
|
Х |
0 |
1 |
Обозначение |
Наименование |
|
Y1 |
0 |
0 |
0 |
Константа 0 |
|
Y2 |
0 |
1 |
Х |
Повторение Х |
|
Y3 |
1 |
0 |
/Х |
Инверсия Х |
|
Y4 |
1 |
1 |
1 |
Константа 1 |
Рис. 1.2. - Булевы функции одного аргумента
Вторая функция из таблицы повторяет значения аргумента. Она так и называется - повторение. Практического значения не имеет.
Наконец, функция, третья в приведенной таблице и принимающая значения, противоположные значениям аргумента. Она называется инверсия и входит в основной ряд фундаментальных булевых функций.
Булевы функции двух аргументов являются основополагающими для всей цифровой техники и современных приложений. Именно на функциях двух аргументов основаны все современные цифровые технологии и их многочисленные приложения.
Приведем развернутую таблицу булевых функций двух аргументов. Как следует из предыдущего, количество таких функций равно 16. Таблица функций и их описание приведены на рис. 1.3.
Булевы функции двух аргументов приведены на рис. 1.3. Среди них есть и функции одного аргумента. Это прежде всего константы Y0 = 0 и Y15 = 1. Кроме них, известны функции повторения Y3 = X2 и Y5 = X1, а также инверсии Y10 = \X1 и Y12 = \X2. Остальные функции нуждаются в дополнительных комментариях.
|
Х1 |
0 |
1 |
0 |
1 |
Обознач |
Выраж |
Наименование |
|
Х2 |
0 |
0 |
1 |
1 |
|||
|
Y0 |
0 |
0 |
0 |
0 |
Y=0 |
Х|X |
Константа 0 |
|
Y1 |
0 |
0 |
0 |
1 |
X1&X2 |
X1X2 |
Конъюнкция |
|
Y2 |
0 |
0 |
1 |
0 |
Х2←Х1 |
|X1X2 |
Запрет по Х1 |
|
Y3 |
0 |
0 |
1 |
1 |
X2 |
X2 |
Повторение Х2 |
|
Y4 |
0 |
1 |
0 |
0 |
Х1←Х2 |
X1|X2 |
Запрет по Х2 |
|
Y5 |
0 |
1 |
0 |
1 |
X1 |
X1 |
Повторение Х1 |
|
Y6 |
0 |
1 |
1 |
0 |
X1ѲX2 |
X1|X2+|X1X2 |
Неравнозначность |
|
Y7 |
0 |
1 |
1 |
1 |
X1+X2 |
X1+X2 |
Дизъюнкция |
|
Y8 |
1 |
0 |
0 |
0 |
Х1\ Х2 |
|X1|X2 |
Штрих Шеффера |
|
Y9 |
1 |
0 |
0 |
1 |
Х1≈Х2 |
X1X2+|X1|X2 |
Равнозначность |
|
Y10 |
1 |
0 |
1 |
0 |
│Х1 |
|X1 |
Инверсия Х1 |
|
Y11 |
1 |
0 |
1 |
1 |
Х2→Х1 |
|X1+X2 |
Имплик. от Х2 к Х1 |
|
Y12 |
1 |
1 |
0 |
0 |
│Х2 |
|X2 |
Инверсия Х2 |
|
Y13 |
1 |
1 |
0 |
1 |
Х1→Х2 |
X1+|X2 |
Имплик. от Х1 к Х2 |
|
Y14 |
1 |
1 |
1 |
0 |
X1↓X2 |
|X1|X2 |
Стрелка Пирса |
|
Y15 |
1 |
1 |
1 |
1 |
Y=1 |
X + |X |
Константа 1 |
Рисунок 1.3 - Булевы функции двух аргументов
Функция Y1 принимает значение 1 только в случае, когда оба аргумента равны 1. Она называется логическое умножение или конъюнкция и имеет большое прикладное значение. Ее также называют функция И.
Функция Y7 равна 1, если хотя бы один из аргументов принимает значение 1. Это логическое сложение, или дизъюнкция, а также функция ИЛИ.
Функция Y9 принимает значение 1, если оба аргумента одинаковы, или1, или 0. Это равнозначность.
Обратная равнозначности функция – неравнозначность, Y6. или исключающее ИЛИ. Функция также носит название сложение по модулю 2 и имеет большое прикладное значение в цифровых технологиях.
Очень важное значение имеют функции Y8 и Y14. Первая, штрих Шеффера, принимает значение 1 только в случае, если оба аргумента равны 0, и называется еще функцией И – НЕ; вторая, равная 0 только при обоих аргументах, равных 1, носит название стрелка Пирса, но чаще называется ИЛИ – НЕ. При проектировании ПЛИС они имеют первостепенное значение (и не только в ПЛИС: микропроцессоры, системы электронной памяти и цифрового управления в качестве базовых элементов используют триггеры, о которых будет сказано впоследствии. Они строятся на схемах И - НЕ и ИЛИ - НЕ).
Перечисленные выше функции относятся к классу симметричных: они не меняют значения при перемене значений аргументов (например, Х1&Х2 = Х2&Х1; Х1≈Х2 = Х2≈Х1 и т.д.). Четыре оставшиеся функции являются несимметричными. Рассмотрим, в частности, функцию Y2. Если Х1 равен 1, Y = 0, при Х1=0 Y повторяет значения Х2. Функция носит название запрет по Х1. Аналогично Y4 является запретом по Х2.
Функции Y11 и Y13 являются взаимообратными относительно Y4 и Y2 соответственно. Они называются импликацией и используются сравнительно редко.
В булевой алгебре важной задачей является отыскание возможности выражения функций через другие. Это позволяет сокращать запись логических выражений и в конечном итоге упростить аппаратную реализацию (следовательно, повысить надежность технических систем).
Обратим внимание, что, если между функциями Y7 и Y8 провести горизонтальную линию, то функции, размещенные симметрично относительно нее, являются взаимно инверсными. Например, Y0 = \Y15 ; Y1 = \Y14 и т.д.
В булевой алгебре вводится понятие функционально полная система: такой набор, с помощью которого можно описать любую функцию любого числа аргументов. Доказано, что для такого набора достаточно не больше четырех функций. Наиболее распространен набор из трех функций: И, ИЛИ, НЕ. Его особенностью является прежде всего то, что он вытекает непосредственно из алгебры множеств, предшественницы алгебры логики. Алгебра, основанная на этой системе функций, называется исчислением высказываний. Она основана на системе аксиом, т.е., правил, не доказываемых в рамках этой алгебры и являющихся основой для дальнейших преобразований и доказательства теорем.
Кроме того, в исчислении высказываний справедлив принцип двойственности: любое алгебраическое выражение выражает ту же функцию, если в нем заменить операции умножения на сложение и наоборот, нули на единицы и наоборот.
Таблица аксиом исчисления высказываний приведена на рис. 3. Она включает две группы аксиом, относительно логического умножения & и логического сложения +. Для упрощения записи знаки &, как в обычной алгебре, опускаются.
Часть аксиом несамостоятельна, т.е. может доказываться на основе других. Они в совокупности представляют повторение алгебры множеств и в дальнейшем будут использоваться при эквивалентных алгебраических преобразованиях.
|
& |
Наименование |
+ |
|
Х1Х2 = Х2Х1 |
коммутативность |
Х1+Х2 = Х2+Х1 |
|
Х1(Х2Х3) = (Х1Х2)Х |
ассоциативность |
(Х1+Х2) +Х3 = Х1+(Х2+Х3) |
|
Х1(Х2+Х3)=Х1Х2 + Х1Х3 |
дистрибутивность |
Х1+(Х2Х3) = (Х1+Х2)(Х1+Х3) |
|
ХХХ……Х=Х |
идемпотентность |
Х+Х+Х+…..+Х=Х |
|
//Х=Х |
||
|
Х&/Х= 0 |
Х+/Х=1 |
|
|
Х&1=Х |
Х+0=Х |
|
|
Х&0=0 |
Х+1=1 |
|
|
/(Х1Х2) = /Х1+/Х2 |
Де Моргана |
/(Х1+Х2) = /Х1/Х2 |
Рисунок 1.4 – Аксиомы булевой алгебры
Возможны и другие функционально полные системы. В частности, функции Y8 (И-НЕ) и Y14 (ИЛИ-НЕ) каждая представляют функционально полную систему, но получаемые при этом выражения намного длиннее, чем при использовании классического исчисления высказываний. Кроме того, для исчисления высказываний разработан мощный математический аппарат, используемый в ряде программных продуктов, в том числе в САПР.
Совершенные нормальные формы
Являются как доказательством возможности описания любой булевой функции, так и основанием для их упрощения.
Существуют две основных формы такого описания: совершенная дизъюнктивная нормальная форма (сокращенно СДНФ) и совершенная конъюнктивная нормальная форма, или СКНФ. Более предпочтительна СДНФ, на которой мы и остановимся.
Дальнейшее описание лучше делать на конкретном примере. Опишем произвольную функцию трех аргументов с помощью таблицы, приведенной на рис. 1.5.
|
Х3 |
Х2 |
Х1 |
Y |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
Рисунок 1.5. – Пример функции трех аргументов
Введем теперь определение конституента единицы. Это произведение всех аргументов, причем значению 1 аргумента в записи произведения будет сам аргумент, а значению 0 – его инверсия. Так, вторая строка таблицы с координатами 001 соответствует конституенте /Х3/Х2Х1. В соответствии с аксиомой коммутативности чаще пишут аргументы в порядке возрастания индексов, т.е. Х1/Х2/Х3.
СДНФ представляет собой дизъюнкцию всех конституент, для которых описываемая функция равна 1. В данном примере в описание входят 5 конституент, а общая запись принимает вид:
Y = Х1/Х2/Х3 + Х1Х2/Х3 + /Х1/Х2Х3 + Х1/Х2Х3 + Х1Х2Х3
Чтобы доказать равенство левой и правой частей, достаточно подставить в них все возможные точки из области определения функции. При этом используется следующее свойство конституенты: она равна 1 только для одного набора значений аргументов, называемого соответствующим. Нетрудно убедиться, что при такой записи СДНФ левая и правая части совпадают.
СКНФ булевой функции проще получить из СДНФ, используя принцип двойственности: достаточно получить СДНФ, после чего заменить умножения сложениями и наоборот. Так, для приведенной выше функции СКНФ будет иметь вид:
Y = (Х1+/Х2+/Х3)(Х1+Х2+/Х3)(/Х1+/Х2+Х3)(Х1+Х2+Х3).
Эта форма по некоторым причинам не нашла особого применения.
Попробуем провести упрощение приведенной СДНФ, используя алгебраические преобразования. Объединим первый член со вторым, а третий – с четвертым:
Y= Х1/Х3(/Х2+Х2) + /Х2Х3(/Х1+Х1) + Х1Х2Х3.
Выражения в скобках равны 1, поэтому окончательно:
Y = Х1/Х3 + /Х2Х3 + Х1Х2Х3.
Мы получили сокращенную ДНФ, но она не обязательно минимальна, так как при алгебраическом сокращении снижаются возможности манипулирования, так как сокращенные произведения могут не участвовать в дальнейших преобразованиях. Известно, что для получения наиболее короткой записи (т.е. для минимизации) необходимы неалгебраические методы. Некоторые мы и рассмотрим.
Методы минимизации булевых функций
Для описания методов минимизации необходимо ввести понятие накрытия. Пусть заданы две функции, Y1 и Y2. При произвольном наборе аргументов обе функции принимают одно из двух значений, 0 или 1. При этом, если значения функций совпадают и равны 1, говорят, что функция Y2 накрывает своей единицей функцию Y1. Для минимизации необходимо и достаточно, чтобы единицы минимальной функции накрывали все единицы исходной. При этом допускается неоднократное накрытие некоторых единиц, что и составляет «изюминку» неалгебраических методов.
Следует помнить, что при минимизации теряется взаимно однозначное соответствие: одной функции может соответствовать две и больше минимальных.
Геометрический метод минимизации
В основе геометрического метода лежит представление области определения булевой функции как вершин К – мерного куба. Наиболее наглядно это выглядит для К=3, т.е. для куба в классическом представлении.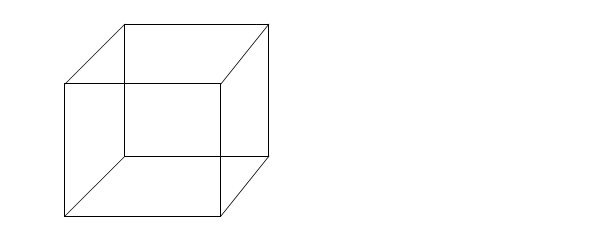
Рисунок 1.6. – Разметка трехмерного куба (а) и нанесение единиц (б)
На рис. 1.6,а показана разметка трехмерного куба с координатами вершин. Дадим дополнительные объяснения модели. Каждая вершина трехмерного куба имеет три координаты, Х1, Х2 и Х3. Совокупность этих координат сопоставляется с трехбуквенным произведением, причем если аргумент в этой точке равен 1, соответствующий аргумент записывается без инверсии, если 0 – с инверсией. Так, точке А соответствует произведение /Х1/Х2/Х3; точке С – Х1Х2/Х3; точке Н - /Х1Х2Х3.
Любое ребро на кубе (а их всего 12) соединяет две смежные точки и соответствует двухбуквенному произведению, для которого две координаты неизменны. Например, ребру DH соответствует произведение /Х1Х2; ВС – Х1/Х3.
Грани на кубе (всего их 8) накрываются однобуквенными произведениями, соответствующими аргументам, не меняющимся на этой грани. Так, BFGC накрывается аргументом Х1, EHGF – Х3, HGFE – Х2.
Тогда алгоритм минимизации функции трех аргументов запишется в виде.
1. Размещаем единицы исходной функции в вершинах трехмерного куба.
2. Ищем на кубе грани с единицами во всех вершинах и накрываем их однобуквенными произведениями.
3. Среди оставшихся не накрытыми единиц ищем ребра с единицами в вершинах и накрываем их двухбуквенными произведениями.
4. Оставшиеся одиночные единицы накрываются трехбуквенными произведениями.
Применим алгоритм к приведенной в качестве примера функции. Размещаем на кубе единицы и помечаем их, как показано на рис. 1.6, б (п. 1 алгоритма). Ищем и находим грань с единицами: это ABED. Накрываем грань однобуквенным произведением Х1. Оставшуюся не накрытой единицу С объединяем с D и накрываем произведением /Х2Х3. Таким образом, окончательно Y = Х1 + /Х2Х3.
Как видим, для функции трех аргументов геометрический метод достаточно прост и эффективен. Наиболее сложным является вариант, когда для функции с 6 единицами нули размещены на главной диагонали. Таких вариантов 4. Рассмотрим один из них (см. рис. 1.6 в). Граней с единицами здесь нет, т.е. отсутствуют однобуквенные произведения. Зато существует два варианта минимизации с использованием граней. Первый соответствует набору ребер, помеченных одним штрихом, второй – двумя. Легко можно получить эти варианты:
Y1 = |X2X3 + X1X2 + |X1|X3 ;
Y2 = |X1|X2 + X1C3 + X2|X3 .
Отсюда видно, что при минимизации теряется взаимно однозначное соответствие.
Прежде, чем переходить к интерпретации геометрического метода для функций с числом аргументов больше 3, приведем алгоритм построения куба мерности К+1. Для этого изображаются два куба мерности К, после чего ребрами соединяются все их соответствующие вершины. В качестве примера на рис. 1.7 приведено построение четырехмерного куба. Несмотря на внешнюю простоту построения, трудно представить такой куб.
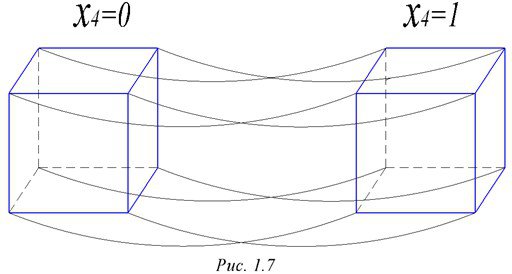
Рисунок 1.7.- Графическое представление четырехмерного куба
Обобщенный алгоритм минимизации функции К аргументов записывается в следующей форме.
1. На вершины К – мерного куба наносятся единицы исходной функции.
2. На К – мерном кубе ищутся кубы мерности К-1 с единичными вершинами. Они накрываются однобуквенными произведениями.
3. Среди оставшихся не накрытыми ищутся единицы, лежащие в вершинах кубов мерности К-2 и накрываются дкухбуквенными произведениями.
……………………………………………………………………………..
К+1 Одиночные единицы накрываются К – буквенными произведениями .
Геометрический метод, хотя и претендует на наглядность, трудно формализуется.
Метод Карно
Метод хорош для функций 3 и 4 аргументов. Классическим считается четырехмерный вариант. Для реализации метода строится специальная таблица – карта Карно. Она приведена на рис. 1.8, а.
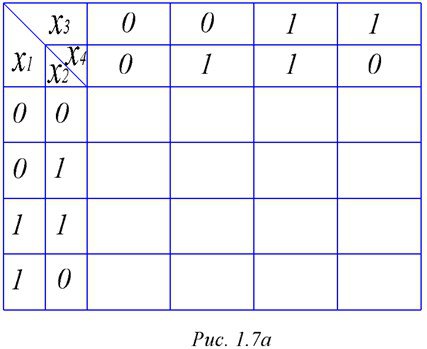
Рисунок 1.8. – Карта Карно
Собственно карта – это квадратная таблица, отделенная жирными линиями. Дополнительные поля образуют сетку координат. Координаты записаны таким образом, что основное поле находится на поверхности воображаемого тора. При этом на поверхности тора соседними являются первая и последняя строка таблицы и ее первый и последний столбцы.
Упрощенное изображение карты Карно показано на рис. 1.8, б. Здесь линиями показаны строки (столбцы), для которых соответствующие аргументы равны 1.
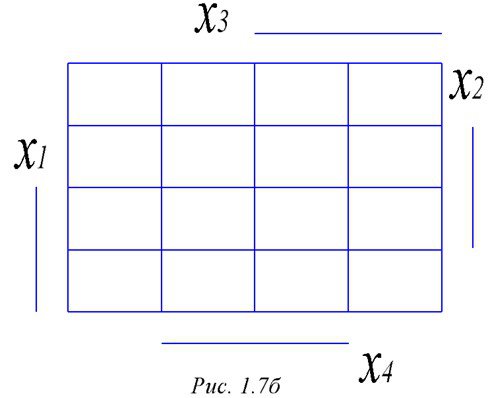
На карте Карно своеобразное понятие соседства. Соседними являются первая и последняя строка и первый и последний столбцы, так как таблица размещена на торе.
После такой преамбулы можно сформулировать собственно алгоритм минимизации. Для этого воспользуемся примером функции четырех аргументов, заданной в виде сокращенной ДНФ:
Y = /Х1Х2Х4 + Х1/Х2Х3 + Х1/Х2Х4 + Х1Х2/Х4 +/Х1/Х2Х4 +/Х2/Х3Х4
Необходимо привести эту функцию к СДНФ, для чего воспользуемся следующим приемом: для привлечения недостающего аргумента домножим каждую сокращенную форму на сумму недостающего аргумента и его инверсии. В частности, первый член предыдущего выражения преобразуется к виду:
/Х1Х2Х4 = /Х1Х2Х4(Х3+/Х3) = /Х1Х2Х3Х4 + /Х1Х2/Х3Х4
Продолжая эту процедуру для оставшихся членов сокращенной формы, в итоге получаем СДНФ:
Y = |X1X2X3X4 + |X1X2|X3X4 + X1|X2X3X4 + X1|X2X3|X4 + X1|X2|X3X4 + X1X2X3|X4 + X1X2|X3|X4 + |X1|X2X3X4 + |X1|X2|X3X4
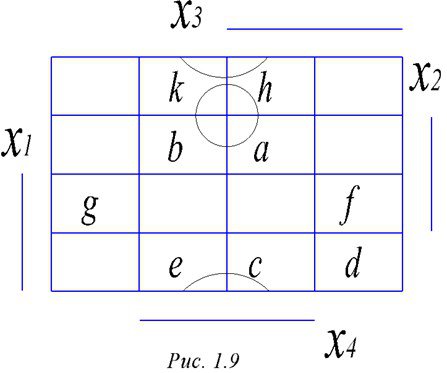
Размещаем теперь конституенты на карту Карно (см. рис.1.9).
Сформулируем теперь сам алгоритм.
1. Наносим единицы функции на карту Карно
2. Ищем на карте группы из 8 соседних единиц. Это или две соседние строки с единицами, или два соседних столбца. Они накрываются однобуквенными произведениями, для которых соответствующий аргумент неизменен.
3. Из оставшихся не накрытыми единиц ищем группы из четырех соседних. Это или строка, или столбец, или квадрат на торе. Они заменяются двухбуквенными произведениями.
4. Из оставшихся не накрытыми ищем группы из двух соседних единиц и накрываем их трехбуквенными произведениями.
5. Одиночные единицы накрываются четырехбуквенными произведениями.
Применим этот алгоритм к нашему примеру (см.рис. 1.9). Групп из 8 элементов не обнаруживается. Зато есть две группы из 4 элементов: abkh (соответствует произведению \Х1Х4) и khec (произведение /Х2Х4). Оставшиеся единицы накрываются трехбуквенными произведениями: fd (Х1Х3/Х4) и fg (X1X3|X4). Таким образом минимальная ДНФ имеет вид:
Y = |X1X4 + |X2X4 + X1X3|X4 + X1X3|X4.
Возможен и второй вариант минимальной ДНФ, если выбрать другой вариант двухбуквенных накрытий: cd и fg. Тогда получим:
Y = |X1X4 + |X2X4 + X1X3|X4 + Х1/Х2Х3.
С помощью карт Карно возможна минимизация и функций трех аргументов. Карта в этом случае приобретает вид, показанный на рис. 1.10.
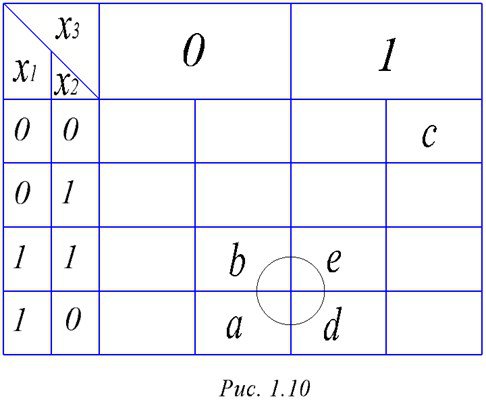
Основное поле , обведенное жирной линией, размещается на поверхности цилиндра, на которой соседними являются первая и последняя строка. Алгоритм минимизации такой же, только пропущен п.2. В качестве примера рассмотрим ту же функцию, что и при рассмотрении геометрического метода минимизации. Размещение единиц показано на том же рисунке с теми же обозначениями. Ищем и находим группу из 4 соседних единиц: beda. Накрываем ее однобуквенным произведением Х1. Оставшуюся ненакрытой единицу с объединяем с d, что соответствует двухбуквенному произведению /Х2Х3. Итак, Y = X1 + |X2Х3, что совпадает с результатами минимизации геометрическим методом.
К сожалению, метод Карно ограничен рамками нашего восприятия. Уже для К=5 трудно представить четырехмерную поверхность и тем более отношения соседства на ней.
Метод Квайна
В отличие от предыдущих методов минимизации, метод Квайна позволяет минимизировать функции произвольного числа аргументов. Плата за это – излишняя громоздкость. С другой стороны, метод легче формализовать и следовательно автоматизировать.
Метод основан на двух процедурах: неполного склеивания и поглощения. Аксиома неполного склеивания имеет вид:
Ах + А/х = Ах + А/х +А.
Здесь под А подразумевается любое алгебраическое выражение, в том числе и произведение нескольких аргументов. Правую часть можно упростить и довести ее просто до А, но это не делается сознательно. Несмотря на кажущуюся тавтологию, аксиома имеет смысл вследствие того, что в этом случае не теряются сокращаемые члены, как в обычной алгебре. Благодаря этому возможно исследование всех вариантов сокращения с последующим выбором оптимального. Для выбора используется вторая аксиома, поглощения:
АХ +А = А
Она очевидна и используется на втором этапе минимизации. Суть ее состоит в том, что после цепочки неполных склеиваний в конечной записи остаются только те произведения, которые не подвергались склеиваниям на предыдущих этапах.
Наконец, на завершающем этапе минимизации строится таблица Квайна, с помощью которой делается окончательный выбор минимальной ДНФ.
Проиллюстрируем алгоритм на примере функции четырех аргументов, задав ее таблично (см. рис. 1.11).
|
Х4 |
Х3 |
Х2 |
Х1 |
Y |
|
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
Рисунок 1.11. - Функция четырех аргументов
Запишем ее СДНФ:
Y = |X1|X2|X3|X41 + X1|X2|X3|X42 + |X1X2X3|X43 + X1X2X3|X44 + |X1|X2|X3X45 + X1|X2|X3X46 + |X1|X2X3X47 + X1|X2X3X48 .
В выражении каждая конституента пронумерована для дальнейшего облегчения преобразований.
Первым шагом алгоритма является просмотр возможностей неполного склеивания. Для этого необходимо, чтобы претенденты на склеивание имели одинаковую длину, одинаковые аргументы и отличались друг от друга только в одном аргументе, причем этот аргумент в одном произведении был без инверсии, а во втором – с инверсией. Просмотр лучше проводить с начала списка.
Итак, первый член СДНФ можно склеить со вторым:
/Х1/Х2/Х3/Х4 + Х1/Х2/Х3/Х4 = А + /Х2/Х3/Х4.
Здесь А – выражение слева. Кроме того, первый член склеивается и с пятым:
/Х1/Х2/Х3/Х4 + /Х1/Х2/Х3Х4 = В + /Х1/Х2/Х3.
Продолжая ту же процедуру, проводим следующие склеивания: 2 и 6; 3 и 4; 5 и 6; 6 и 8; 7 и 8. В результате получаем:
Y = Q + |X2|X3|X49 + |X1|X2|X310 + X1|X2|X311 + Z2Z3|X412 + |X1|X2X413 + |X2|X3X414 + X1|X2X415 + |X2X3X416 .
Продолжаем склеивания в полученных сокращенных формах, помня упомянутое выше правило. При этом возможно склеивание следующих проиндексированных членов: 9 и 14, 13 и 15, 14 и 16. Получается выражение:
Y = W + |X2|X3 + |X2X4 + |X3X4.
Отметим, что на первом этапе склеиваний участвовали все члены СДНФ, а на втором не участвовали члены с номерами 10, 11 и 12. При составлении таблицы Квайна они должны учитываться.
Таблица Квайна строится следующим образом. Первый столбец содержит сокращенные формы, оставшиеся после поглощения. Первая строка перечисляет все конституенты СДНФ. Тело таблицы заполняется так: если рассматриваемая сокращенная форма входит в состав данной конституенты, на пересечении ставится значок (например, +) , если нет, делается пропуск. На рис. 10 приведена таблица для рассматриваемого примера.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|X2|X3 |
+ |
+ |
+ |
+ |
||||
|
|X2X4 |
+ |
+ |
+ |
+ |
||||
|
X1|X2|X3 |
+ |
+ |
||||||
|
X2X3|X4 |
+ |
+ |
Рисунок 1.12. – Таблица Квайна
Необходимо, чтобы минимальным набором сокращенных произведений накрывались все столбцы. Формальное правило требует, что в минимальную форму обязательно входили такие сокращенные произведения, которые содержат хотя бы один плюсик, единственный в одном из столбцов. В нашем примере это первое, второе и четвертое произведение. Третье можно исключить как избыточное. Таким образом, минимальная ДНФ имеет вид:
Y = |X2|X3 + |X2X4 + X2X3|X4
Элементы теории конечных автоматов
Теория конечных автоматов была разработана в средине ХХ века группой ученых, в состав которой входили Н.Винер, А.Тюринг, Дж. Фон Нейман и др. Созданная ими теория послужила основанием для создания всего семейства цифровой техники. ПЛИС также входят в это семейство.
Конечный автомат (КА) является частным случаем конечной динамической системы (КДС). Последняя имеет следующие отличительные признаки:
1. Она работает в дискретные моменты времени, называемые тактами. Такты могут определяться с одинаковыми временными интервалами или с различным шагом во времени. Соответственно различают системы с равномерной и неравномерной тактностью. В общем случае тактом можно объявлять любой момент времени, в который происходит какое – то изменение или на входе или выходе системы или внутри самой системы.
2. КДС имеет конечное число входов и выходов. Количество состояний по каждому входу (т.е. количество различных входных воздействий), а также количество различных выходных состояний КДС также конечно.
3. Реакция КДС на входные воздействия также конечна, т.е. длится конечное число тактов.
Под понятие КДС можно подвести практически любое цифровое устройство. Исключением могут являться, например, генераторы или таймеры (да и то в случае, если они не имеют входов управления).
КА можно считать простейшим вариантом КДС по крайней мере по одному показателю: его динамические свойства распространяются только на два соседних такта. Один из них называется настоящее (Н), второй – прошлое (П).
Различают два типа КА. Первый тип обладает следующим свойством: его текущее состояние (т.е. в такт Н) зависит от предыдущего состояния и воздействия на него в настоящее время. Такой КА называется автоматом типа П – Н, или автоматом Мура. Второй тип зависит также от предыдущего состояния, но от воздействия в предыдущий такт. Это – автоматы типа П – П, или автоматы Мили.
Способы задания конечных автоматов
Существует три основных способа описания (задания) КА. Первый, табличный, является основным. Таблица КА – это прямоугольная таблица размером N*M, где N – количество выходных состояний, а М – количество входных состояний. Пример таблицы приведен на рис. 1.13. Здесь через YI обозначены выходные состояния КА, через XJ- входные воздействия.
|
X1 |
X2 |
X3 |
X4 |
X5 |
|
|
Y1 |
Y2 |
Y4 |
Y1 |
Y4 |
Y1 |
|
Y2 |
Y1 |
Y1 |
Y2 |
Y3 |
Y3 |
|
Y3 |
Y2 |
Y3 |
Y4 |
Y1 |
Y2 |
|
Y4 |
Y1 |
Y1 |
Y4 |
Y2 |
Y4 |
Рисунок 1.13. – Пример таблицы конечного автомата
Принято считать, что между конечным автоматом и его таблицей существует взаимно однозначное соответствие, т.е. таблице соответствует единственный КА и наоборот. Недостатком табличного описания является отсутствие указания типа КА (П – П или П – Н), но это можно указать дополнительно.
Второй тип описания – диаграммы состояния, или диаграммы переходов. Это направленные графы, в которых число вершин равно числу выходных состояний, а направленные дуги соответствуют переходам КА при соответствующем входном воздействии. Воздействия надписываются над дугами, причем для КА типа П –П надписи делаются в началах дуг, а П – Н в концах, Так как граф получается громоздким, допускается кратные дуги заменять одной с записью входного воздействия в виде суммы. Пример диаграммы состояний приведем из таблицы по рис 1.14. Диаграмма приведена в предположении, что автомат – типа П – Н.
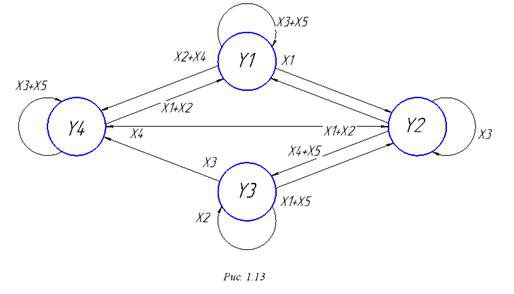
Рисунок 1.13 – Диаграмма состояний конечного автомата
Третий вариант задания КА – перечислением триад – совокупностей троек значений YP-1 XP YP, т.е. предыдущего состояния, воздействия и конечного состояния. Это – для автомата типа П – Н; для автомата П – П в триаду включается ХР-1.
Этот метод используется редко из – за громоздкости, но применяется в задачах синтеза.
Синтез конечных автоматов
Используется разработчиками для разработки и реализации КА по формальному описанию его работы. Такое описание называется лента работы. Это полубесконечная таблица из двух строк: в первой записываются значения ХI , во второй – YJ. По имеющейся записи на ленте осуществляется заполнение таблицы КА, причем способ просмотра ленты зависит от типа КА. Для автоматов типа П – П и П – Н считывание проводится по форме, показанной на рис. 1.14, что соответствует принципам их работы.
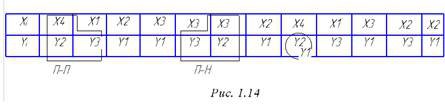
Синтез осуществляется следующим образом. Составляется шаблон таблицы, исходя из списка на ленте и производится заполнение таблицы, начиная с левой ее части. Выбираем автомат типа П – П. Пара X4Y2 имеет результат Y3. Заполняем соответствующий элемент в таблице и смещаем шаблон вправо на шаг. Результат, Y1 также заносим в таблицу. Продолжая заполнение таблицы аналогичным образом, доходим до противоречия: пара X2Y1 по ленте должна давать Y1, но это место в таблице занято элементом Y2. Здесь возможны два решения: или считать КА нереализуемым, или переопределить состояние на ленте. Выберем второй вариант: заменим элемент на ленте табличным вариантом и продолжим просмотр. В результате после просмотра выделенного фрагмента ленты таблица принимает вид, показанный на рис. 1.15. Она заполнена не до конца, поэтому нужно или продолжать просмотр, или считать незаполненные ячейки недопустимыми состояниями.

При реализации КА возможны тупиковые ситуации, когда автомат попадает в состояние, из которого нет выхода: при любом входном воздействии его состояние не изменяется. В таких случаях вводится специальное входное состояние Х0 (сброс), которое переводит КА в исходное состояние. Кстати, такое входное воздействие предусмотрено на любом техническом устройстве и называется кнопкой аварийной остановки.
Триггеры как конечные автоматы
С изобретением триггеров произошла техническая революция во всех областях. Для человеческой цивилизации это изобретение можно сопоставить с такими достижениями, как способ добычи и поддержания огня, изобретение рычага и колеса. Совершенство и изящество электронной схемы триггера послужили толчком в развитии средств микроэлектроники, в том числе ПЛИС.
В основном триггеры (Т) являются элементами памяти, элементарной ее ячейкой. Т может иметь два устойчивых состояния, 0 или 1, причем сохраняет это состояние сколько угодно долго. В них используется эффект положительной обратной связи (ПОС), что и обеспечивает их свойства. Они могут быть реализованы на релейно – контактных устройствах, на транзисторах, электронных лампах, полупроводниковых структурах и т.д. Благодаря своей изящной структуре они легко переносятся на любую основу из нанотехнологий.
Рассмотрим простейший тип Т – асинхронные RS – триггеры. Асинхронными они называются вследствие того, что срабатывают сразу при поступлении управляющего сигнала. Они имеют два управляющих входа: S (от слова set – включить) и R (от слова reset – выключить). Любой триггер имеет два устойчивых состояния: 0 или 1. Обычно Т имеет два взаимно инверсных выхода, Q (от слова quit – выход) и |Q.
В дальнейшем будем рассматривать Т, реализованные на элементах И – НЕ и ИЛИ – НЕ. Схема RS – триггера на элементах ИЛИ – НЕ приведена на рис. 1.16. Использованы два элемента 2ИЛИ – НЕ, D1 и D2. Они, как видно из рисунка, охвачены перекрестной ПОС: выход D1 присоединен ко второму входу D2, а выход D2 – ко второму входу D1.
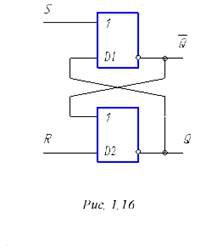
Рисунок 1.16. – Схема RS – триггера 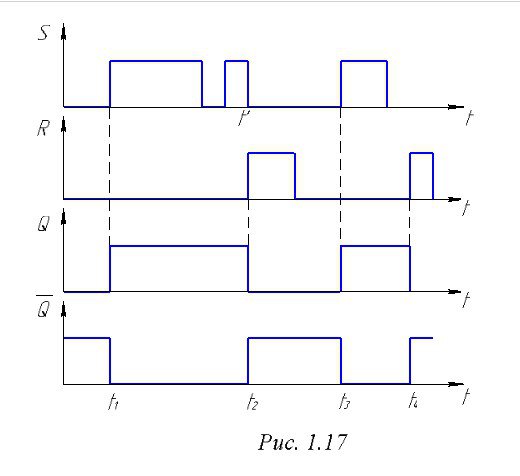
Рисунок 1.17. - Временные диаграммы
На рис. 1.17 приведены временные диаграммы работы триггера. Предположим, вначале триггер находится в состоянии 0: на выходе D2 ноль, на выходе D1- единица. Благодаря тому, что единица с выхода D1 поступает на вход D2, состояние D2 подтверждается, и триггер сохраняет свое состояние.
Если в момент времени t1 на входе S (вход D1) появится единица, элемент D1 переключается в 0, а за счет ПОС с выхода D1 на вход D2 это переключение происходит очень быстро. Повторная подача 1 на вход S (момент времени t1 на временной диаграмме) состояние триггера не меняет. Он будет в единице до поступления управляющего воздействия на S – вход (момент t2 на временной диаграмме). В это время он устанавливается в 0. Дальнейшая часть диаграммы просто повторяет процесс работы триггера.
Обязательным условием устойчивой работы RS – триггера является недопустимость одновременной подачи единиц на оба входа. Такая ситуация называется коллизия и приводит к неопределенному состоянию триггера. Для устранения коллизий иногда используют триггеры с преобладанием или по R, или по S – входу, но такой вариант используется редко.
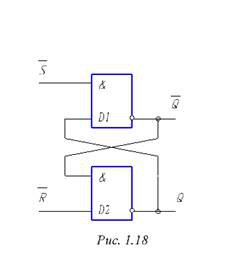
Второй тип RS – триггеров – использование элементов И – НЕ. Схема такого триггера приведена на рис.1.18. В отличие от предыдущего варианта, триггер имеет инверсные входы, т.е. управляется нулями. Здесь запрещенной является одновременная подача нулей на оба входа.
Опишем RS – триггер как конечный автомат. Таблица состояний такого КА будет иметь вид, показанный на рис.1.19. При нулях на входах триггер сохраняет предыдущее состояние, при подаче управляющих воздействий на один из входов он безусловно переключается, а одновременная подача единиц запрещена.
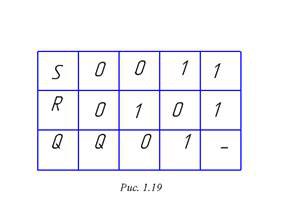
Рисунок 1.19. – Таблица состояний
Диаграмма состояний RS – триггера приведена на рис. 1.20. Из нее видно, во – первых, что триггер относится к КА типа П – Н (надписи - у концов дуг), а во – вторых, что повторная подача управляющего воздействия не изменяет состояния триггера (петли на графе).
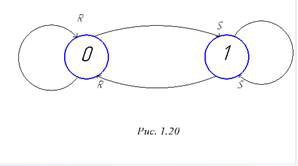
Рисунок 1.20. – Диаграмма состояний
На практике Т часто используются для формирования коротких фронтов импульсов: используется эффект ПОС. Еще одно важное применение Т – устранение «дребезга» контактов. При механическом замыкании или размыкании контактов при наличии напряжения возникают микроэлектрические дуги. Они и называются дребезгом. При маломощной коммутации особого вреда может не наблюдаться, но для работы подключенного к ним оборудования это недопустимо. Для устранения этого эффекта используют свойство триггера не реагировать на повторное управление. Схема такого подключения приведена на рис.1.21.
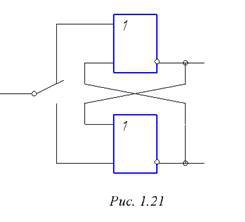
Рисунок 1.20. - Устранение дребезга
Еще один вариант RS – триггеров – введение в них синхронизации. Схема синхронизируемого RS – триггера приведена на рис. 1.22. Схема выполнена на трехвходовых элементах 3И - НЕ. При этом добавляется вход синхронизации С, дающий тот эффект, что переключение триггера возможно только при подаче 0 на вход С импульса синхронизации. Описание Т как конечного автомата не изменяется, только вместо входов R и S появляются входы CR и CS.
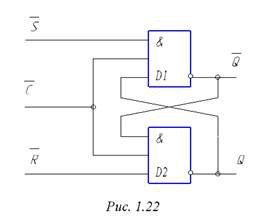
Рисунок 1.22. - Синхронизация триггера
Другая разновидность Т – JK – триггеры. В отличие от триггеров RS, они не имеют запрета на одновременную подачу управляющих воздействий на оба входа. При таком воздействии JK – триггеры переходят в противоположное состояние, что позволяет использовать их в новом качестве.
Таблица состояний JK – триггера показана на рис. 1.23. В отличие от RS, изменился последний элемент нижней строки. На диаграмме состояний (см. рис. 1.24) при неизменном внешнем виде изменились надписи над двумя дугами.
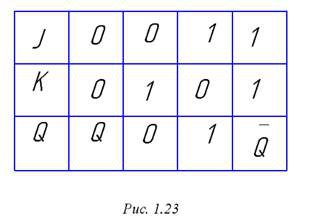
Рисунок 1.23. – Таблица состояний
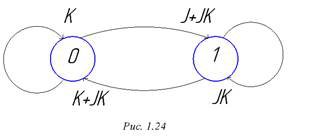
Рисунок 1.24. – Диаграмма состояний
Несмотря на кажущуюся легкость в описании, реализация JK – триггера значительно сложнее, чем RS. На рис. 1.25 приведена схема синхронизируемого JK – триггера с дополнительными установочными входами.
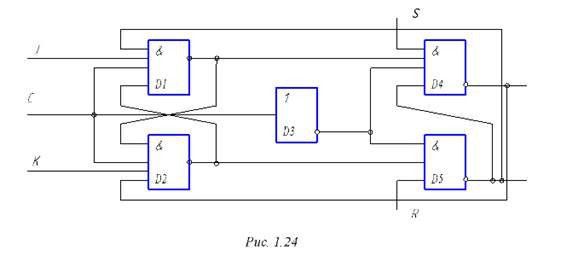
Рисунок 1.25. – Схема синхронизируемого JK – триггера
По структуре триггер двухтактный. Он фактически состоит из двух триггеров: первого на элементах D1и D2 и второго, на элементах D4 и D5. Вход синхронизации С подается через инвертор D3 на вторую часть схемы, что и обеспечивает двухтактность (второй триггер срабатывает по противоположному фронту управляющего импульса). Наличие обратных связей с выхода D5 на вход D1 и с выхода D4 на вход D2 обеспечивает главное отличие триггера, а именно его переход в противоположное состояние при одновременной подаче единиц на входы J и K. Управляющие воздействия S и R на дополнительные входы второго триггера обеспечивают его безусловную установку.
На рис 24,б показано изображение JK – триггера на принципиальных схемах.
Триггеры такого типа используются редко ввиду своей громоздкости. Обычно идут на пути уменьшения количества входов (оставляют один установочный вход, чаще R) или переходят на более практичные D – триггеры.
D – триггер, или триггер задержки, обычно имеет четыре входа: D, C, S и R. Последние являются установочными и необязательными. Сущность работы D – триггера состоит в том, что он переключается по входу С (точнее, по переднему или заднему фронту управляющего импульса на этом входе) и переходит в состояние, которое в этот момент присутствует на входе D. В этом и состоит сущность задержки.
Существует множество практических схем на D – триггерах, часть из которых мы рассмотрим позднее. Пока ограничимся изображением D – триггера на схемах (рис. 25) и включением его в счетном режиме (рис. 26). В последнем случае установочные входы не показаны
Практические приложения ПЛИС
В теории конечных автоматов и цифровых систем принято различать устройства с быстрой и медленной тактностью. В первом варианте используются естественные задержки на срабатывание отдельных вентилей, Этот вариант обеспечивает высокое быстродействие, но имеет и недостатки. Главный из них - необходимость учета пути следования сигналов, и принятия дополнительных мер для синхронизации. При усложнении устройства эта проблема значительно усложняется.
Второй недостаток – усиление зависимости от внешних факторов, особенно от температуры. Время задержки на срабатывание очень сильно зависит от температуры и носит к тому же случайный характер.
Эти недостатки серьезно снижают возможности систем с быстрой тактностью или требуют дополнительных мероприятий по компенсации нежелательных явлений.
Системы с медленной тактностью основаны прежде всего на внешней синхронизации. Это намного снижает риск коллизий и зависимость от внешних условий.
В ПЛИС имеется возможность использовать оба метода за счет их структурной избыточности. Тем не менее, в дальнейшем будет отдаваться предпочтение системам с синхронизацией. Исключение будет делаться только для комбинационных схем.
Комбинационные схемы
Из множества различных комбинационных схем рассмотрим только двоичные шифраторы и дешифраторы. Они нужны для иллюстрации возможностей комбинаторики и послужат в дальнейшем для их программирования.
Двоичные шифраторы предназначены для преобразования позиционного кода в двоичный. Позиционный код – это множество из N входов, на каждом из которых может быть 0 или 1. Количество разрядов двоичного кода К определяется по формуле: К ≥ log2 N.
Предположим, N = 12. Тогда К = 4. Составляем таблицу номеров позиционного кода и эквивалентных им двоичных кодов (рис. 27).
|
№ |
23 |
22 |
21 |
20 |
|
1 |
0 |
0 |
0 |
1 |
|
2 |
0 |
0 |
1 |
0 |
|
3 |
0 |
0 |
1 |
1 |
|
4 |
0 |
1 |
0 |
0 |
|
5 |
0 |
1 |
0 |
1 |
|
6 |
0 |
1 |
1 |
0 |
|
7 |
0 |
1 |
1 |
1 |
|
8 |
1 |
0 |
0 |
0 |
|
9 |
1 |
0 |
0 |
1 |
|
10 |
1 |
0 |
1 |
0 |
|
11 |
1 |
0 |
1 |
1 |
|
12 |
1 |
1 |
0 |
0 |
Рисунок 1.27. – Таблица кодов
Чтобы получить двоичный шифратор, в данном случае необходимо иметь К схем ИЛИ (в данном случае 4) с числом входов у каждой, равным количеству 1 в соответствующем столбце. В данном случае в первом и втором столбцах по 5 единиц, а в третьем и четвертом – по 6,следовательно, необходимы две 5 – входовых и две 6 – входовых схемы ИЛИ. Схема шифратора примет вид, приведенный на рис. 1.28.
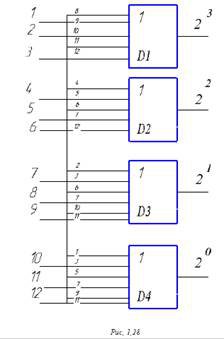
Рисунок 1.28. – Шифратор на 12 входов
При этом может возникнуть сложность, связанная с тем, что таких схем может не быть; тогда они могут синтезироваться из схем с меньшим числом входов. Например, схема ИЛИ на 6 входов при наличии только двухвходовок примет 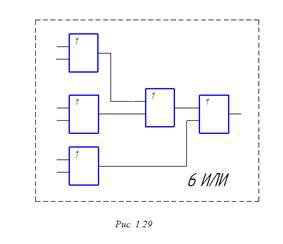 .
.
Рисунок 1.29.- Схема 6 ИЛИ
вид, изображенный на рис. 1.29.
Дешифраторы выполняют функцию, противоположную шифраторам. Они имеют К входов двоичного кода и N выходов позиционного и реализуются на К – входовых схемах И. Количество схем И равно количеству выходов. Дополнительно в них вводятся К инверторов Схема дешифратора кода из предыдущего примера, т.е. (4,12) приведена на рис. 1.30. Для упрощения изображения на входе рисуется жгут. Поясним принцип работы дешифратора по схеме. Он содержит 12 четырехвходовых схем И D1,…D12 и 4 инвертора D12….D16. Логика работы следующая. Допустим, D1 настроен на единицу. Двоичный код единицы 0001. Для того, чтобы сработала схема D1, нужно , чтобы на всех ее входах были единицы. Поэтому младший разряд на вход D1 подключается непосредственно, а старшие – через инверторы. Соответственно и маркировка выходов из жгута: 1.2.3.8. Код цифры 9 – 1001, поэтому маркировка выходов 5,2,3,8.
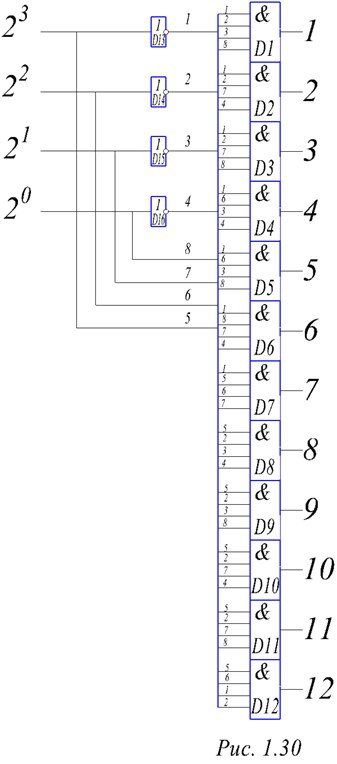
Рисунок 30. – Дешифратор
Для реализации многовходовых схем И используется или параллельное, или каскадное включение. Здесь также возможны варианты. Например, для создания 6 – входовой схемы И из двухвходовок можно применить параллельное включение, как это показано на рис. 31, в можно и каскадное, по типу рис. 32. Последний вариант удобнее для программирования.
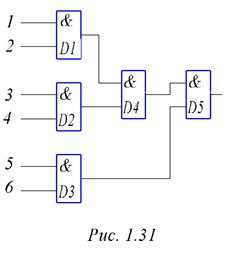
Рисунок 1.31. – Схема 6И
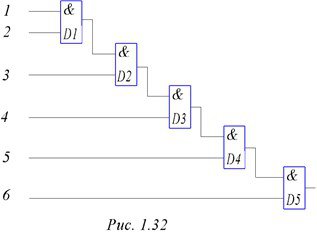
Рисунок 1.32 – Схема 6И, каскадная
Возможности конструирования логических устройств еще больше увеличиваются при использовании схем типа И – НЕ и ИЛИ – НЕ. При этом широко используются аксиомы Де Моргана: |(X1 + X2) = |X1&|X2 и |(X1&X2) = |X1 +|X2. На практике это называется инверсная логика: функция И преобразуется в ИЛИ и наоборот. Например, функцию 7И можно реализовать по типу рис.1.33, а функцию 6ИЛИ – по варианту рис. 1.34. Отметим, что это – не лучшие варианты реализации. Вентили D4 и D8 на рис.1.33 и D7 на рис. 1.34 выполняют функции инверторов и показаны здесь для иллюстрации возможностей схем.
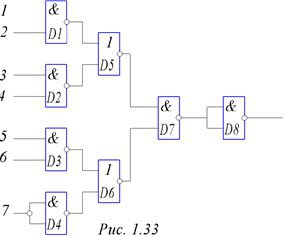
Рисунок 1.33. - Схема 7И, вариант 1
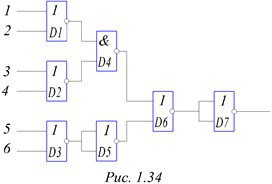
Рисунок 1.34. - Схема 7И, вариант 2
В заключение этого раздела приведем пример реализации ДНФ из ранее приведенного примера раздела «минимизация методом Квайна». Имеем функцию вида:
Y = |X2|X3 + |X2X4 + X2X3|X4 .
Так как осталось для реализации 3 аргумента, устройство имеет три входа и один выход. Схема для его реализации приведена на рис. 1.35. Она содержит 3 инвертора D1, D2 и D3, схемы D4 – D6, реализующие умножения. и D7 для сложения.
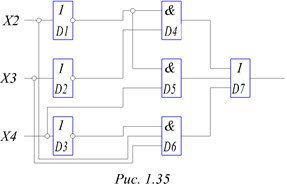
Рисунок 1.35. - Пример реализации ДНФ
Повышенные возможности для инженерного синтеза представляют схемы с использованием триггеров, так как у них имеются и прямые, и инверсные выходы, что предоставляет дополнительные возможности для инженерного синтеза.
При достаточно сложных системах управления возникают проблемы с правильностью реализации. Особенно остро ставятся проблемы с возможными коллизиями из – за различных задержек по времени срабатывания. Недоучет этого может привести к возникновению импульсов помехи или ложным срабатываниям. Простой пример: устройство должно отрабатывать заданное число циклов, которое задается на специальном счетчике. Если на его входе возникают помехи, возникающие из – за недоучета времен задержки по разным каналам, счетчик завершит работу раньше положенного. Найти такие помехи при отладке оборудования очень непросто, так как импульсы очень короткие, и их тем же осциллографом не обнаружить.
Для отладки цифровой техники желательно использовать компьютерное моделирование. В настоящее время существует достаточно большое количество моделирующих пакетов, которые должны быть на вооружении профессиональных инженеров.
Устройства с использованием триггеров
В принципе эта тема достаточно обширна и может рассматриваться в специальных дисциплинах по схемотехнике. Здесь приводится остаточно компактный набор типичных схем, которые впоследствии могут реализовываться на ПЛИС.
Элементы задержки
Задержка нужна для выравнивания фронтов, синхронизации элементов или ля задания технологических пауз в системах управления.
Возможны быстрые и тактируемые (медленные) задержки. Быстрые реализуются последовательным включением нескольких элементов. Время задержки пропорционально количеству элементов в цепочке. Обычно время срабатывания задается в паспорте на ПЛИС и измеряется микросекундами, поэтому диапазон задержек ограничен. Кроме того, время задержки имеет большую случайную составляющую, зависящую к тому же от внешних факторов, особенно от температуры.
Более целесообразна тактируемая задержка. Она реализуется последовательно включенной цепочкой D – триггеров, как показано на рис. 1.36. Количество триггеров S определяет время задержки ТЗ = ST, где Т – период следования тактовых импульсов.
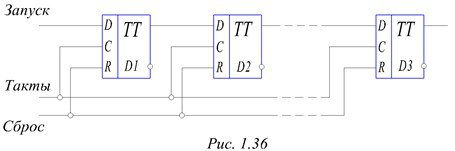
Рисунок 1.36. – Схема задержки на S тактов
Особенностью рассмотренной схемы является то, что длительность управляющих импульсов может быть произвольной; длительность выходных импульсов пропорциональна входным, но кратна Т. Кроме того, путем незначительного усложнения схемы время задержки можно регулировать. Для этого выходы триггеров подключаются через управляемый мультиплексор.
Регистры
Регистры в цифровой технике носят исключительный характер вследствие многообразия выполняемых ими функций. Они могут быть просто элементами памяти, могут выполнять функции преобразователей кода. Они используются как составная часть более сложных устройств, например, микропроцессоров, сложных систем управления, в том числе программируемых.
Обычно принято выделять последовательные и параллельные регистры. Они отличаются методами занесения, хранения и выдачи кодов. Возможны универсальные, последовательно – параллельные регистры.
Аппаратная реализация регистров может быть различной, включая из физическую природу. Мы основной упор сделаем на D – триггерах, поскольку они наиболее благоприятны для ПЛИС.
Универсальный последовательно – параллельный регистр на 4 разряда изображен на рис. 1.37. Регистр состоит из 4 D – триггеров D1 – D4. Вход первого триггера (Вх 1) может служить для ввода последовательного кода. Для этого одновременно с кодом на управляющий вход подаются 4 продвигающих импульса. Требование к ним: они должны подаваться с частотой импульсов последовательного кода, причем желательно, чтобы фронты продвигающих импульсов приходились на средины импульсов входного кода. Это позволит снизить зависимость от дрожания фронтов.
Перед началом работы регистра его нужно очистить, т.е. привести все триггеры в 0, для чего на все их входы R подается импульс «Сброс».
После занесения кода в регистр и прекращения подачи продвигающих импульсов информация в нем может храниться любое время. Ее можно убрать двумя способами: или обычным сбросом (тогда она стирается), или подачей на управляющий вход продвигающих импульсов. Тогда на выходе последовательного кода (Вых 1) появляется код для его приема другими устройствами. Если код в регистр занесен, а продвигающих импульсов нет, регистр по сути выполнил функцию преобразователя последовательного кода в параллельный.
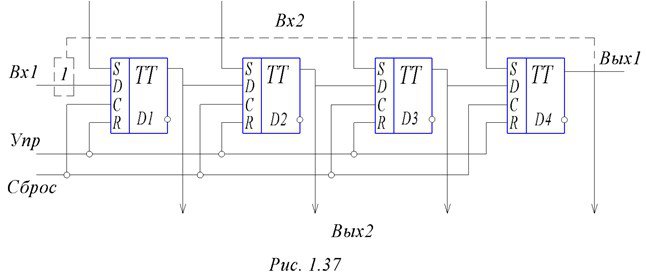
Рисунок 1.37. – Универсальный регистр
Если Вх 1 не задействовать, а подавать параллельный код на входы безусловной установки S, то регистр просто сохранит эту информацию. При этом она может быть считана в любое время, т.е. асинхронно по вых 2 или считается в последовательном коде с Вых 2. При этом регистр очищается. Это и есть преобразование параллельного кода в последовательный.
Возможен и такой вариант включения. На входе устанавливается схема ИЛИ (показана штриховой линией). Если в регистр занести код по последовательному или параллельному входу, а потом подавать на управляющий вход тактовые импульсы, образуется динамический регистр, в котором этот код циркулирует до сброса.
При использовании ПЛИС легко можно увеличить емкость такого регистра до любого нужного числа разрядов.
На электрических схемах регистры часто изображаются в виде, приведенном на рис. 1.39. В особых комментариях это изображение не нуждается.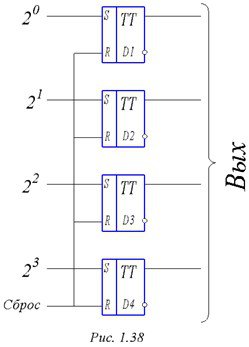
Рисунок 1.38. - Параллельный регистр
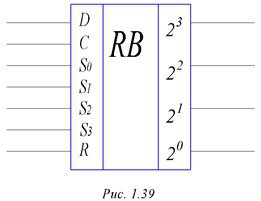
Рисунок 1. 39 - Изображение регистра
Счетчики
Среди множества различных типов счетчиков рассмотрим простейший – счетчик двоичного кода на D – триггерах. Схема четырехразрядного двоичного счетчика приведена на рис. 1.40. D –триггеры D1…. D4 работают в счетном режиме за счет обратных связей на D – входы. Триггеры включены последовательно, в результате чего каждый последующий триггер образует как бы старший разряд относительно предыдущего. Общая шина «Сброс» заводится на все R - входы триггеров. Счетчик легко можно синтезировать на любое число разрядов.
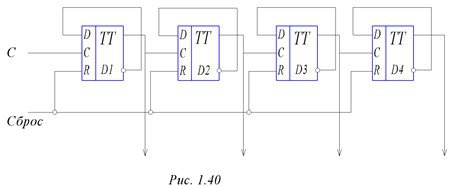
Рисунок 1.40. - Четырехразрядный двоичный счетчик
На рис. 1.41 показано изображение счетчика на принципиальных схемах.
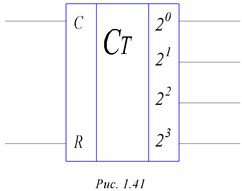
Рисунок 1.41. – Изображение счетчика
Распределители импульсов
Это специализированные устройства с одним тактовым входом и несколькими выходами, причем в каждый момент времени единица присутствует только на одном из входов, а переключение выходов делается поочередно. Распределители (Р) предназначены для управления сложными системами путем разнесения очередности выполнения ими операций во времени.
Возможны два варианта реализации распределителей: на D – триггерах и на счетчиках с дешифраторами. Первый вариант, на D – триггерах, приведен на рис. 1.42. Триггеры D1 – D3 образуют последовательную сдвиговую цепочку, а элементы D4 и D5 реализуют обратную связь для автоматического продолжения работы. При подаче импульса «Запуск» единица последовательно перемещается по цепочке триггеров. Когда единица проходит последний триггер, на выходе D4 появляется 1, повторно запускающая схему. Обязательное условие при этом – ограничение на длительность запускающих импульсов. Если она превышает период тактовой частоты. Выходные импульсы распределителя взаимно перекрываются.
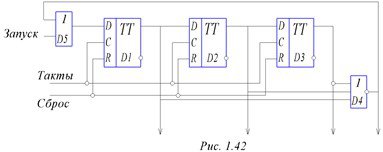
Рисунок 1.42. - Распределитель импульсов на D - триггерах
Второй вариант распределителя приведен на рис.1.43. При подаче тактовых импульсов на вход С счетчика коды на его выходах последовательно возрастают, в результате чего на выходах дешифратора последовательно появляются импульсы. Схема сложнее предыдущей, но работает более надежно.
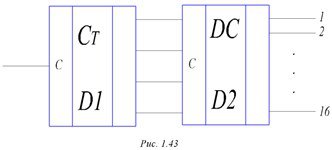
Рисунок 1.43. - Распределитель, 2 вар.
Генераторы псевдослучайных последовательностей
Генераторы псевдослучайных последовательностей (далее ПСП) являются очень важной составляющей инженерной практики. Они используются в множестве практических приложений, в том числе при испытании новой техники, моделировании внешних воздействий, отказов элементов и т.д.
Генераторы ПСП объективно сравниваются по следующим характеристикам.
1. Период повторения ТП. Как правило, после некоторого цикла работы выходные коды генератора повторяются. Чем длиннее период, тем качественнее генератор. Если генератор вырабатывает кодовые последовательности размером в R разрядов, максимальный период повторения составляет 2Rслов.
Похожие работы
... завершенную автоматную структуру, ориентированную на реализацию как комбинационных (дешифраторов,мультиплексоров, сумматоров), так и последовательностных схем (управляющих автоматов, контроллеров, счетчиков). В ПЛИС заложены возможновти, которые позволяют превратить ее в ИС с любой функцией цифровой логики. Проектирование сводится к выявлению программируемых элементов (перемычек или запоминающих ...
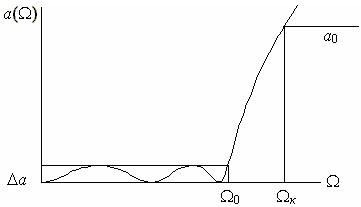
... диаграмм с сохранением результатов в стандартном формате VCD (Value Change Dump), воспринимаемом всеми системами работы с временными диаграммами. [1] 2.МЕТОД ПРОЕКТИРОВАНИЯ УСТРОЙСТВ ФИЛЬТРАЦИИ ПО РАБОЧИМ ПАРАМЕТРАМ Методика проектирования фильтров по рабочим параметрам основана на нахождении значений элементов, нармированных по частоте и сопротивлению нагрузки, путём аппроксимации или с ...
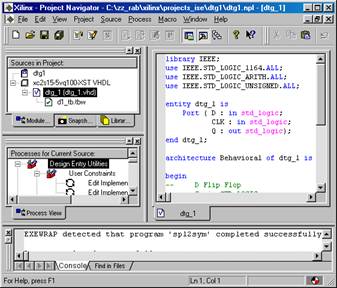
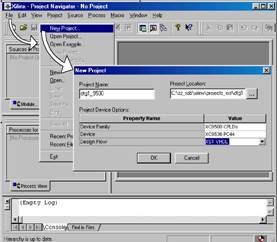
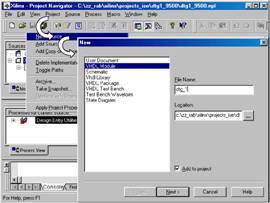
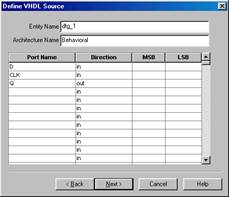
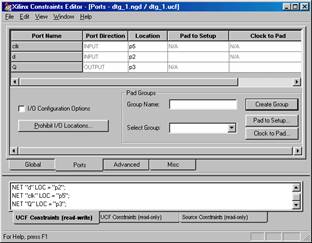
... элементов на кристалле и трассировки связей. 1. Ввод проекта Основные методы и приемы работы с САПР ISE рассмотрим на примере простейшей схемы D –триггера. Использование простейшей схемы позволяет отвлечься от особенностей самой схемы и сосредоточиться только на самом процессе проектирования. Создание нового проекта инициируется последовательным выбором пунктов меню File Þ New ...
... один почти неизвестный в России, но достаточно мощный и популярный в мире продукт - Visula компании Zuken. Продукты этой компании обеспечивают сквозной цикл проектирования и предлагают мощные средства моделирования и синтеза программируемой логики с последующей разработкой печатной платы. Здесь имеется стандартный набор инструментария, а также собственные средства авторазмещения и автотрассировки ...
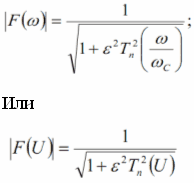
0 комментариев