Лекция
ЛИНЕЙНЫЙ ПЛОСКИЙ ТРЕУГОЛЬНЫЙ ЭЛЕМЕНТ
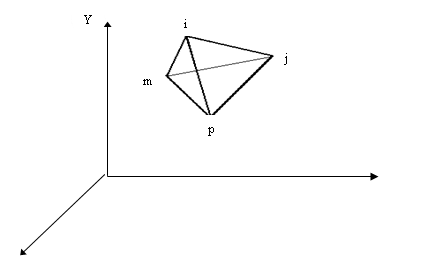
Схема элемента показана на рис.3.1. Элемент имеет три узла, перенумерованные против часовой стрелки. Каждый узел имеет две степени свободы, т. е. может иметь перемещения вдоль осей ![]() и
и ![]() . Предполагается, что смещения
. Предполагается, что смещения ![]() любой точки внутри элемента являются линейными функциями координат этой точки:
любой точки внутри элемента являются линейными функциями координат этой точки:
![]()
![]() (3.16)
(3.16)
где ![]() константы.
константы.

Рис. 3.1
Из (3.16), учитывая (1.14), можно получить выражения для деформаций.
![]()
![]() (3.17)
(3.17)
Из (3.17) следует, что деформации здесь не зависят от координат точки, т. е. являются постоянными в пределах элемента. В связи с этим такой линейный трех узловой элемент получил название «элемента постоянных деформаций».
Заметим, что перемещения самих узлов также должны описываться уравнениями (3.16), при этом вместо ![]() и
и ![]() должны быть подставлены соответствующие координаты узлов
должны быть подставлены соответствующие координаты узлов ![]() . Получим систему шести уравнений, из которой определим шесть искомых коэффициентов
. Получим систему шести уравнений, из которой определим шесть искомых коэффициентов ![]() :
:
![]()
![]()
![]()
![]()
Решив эту систему уравнений, получим выражения для ![]() в зависимости от перемещений узлов и их координат.
в зависимости от перемещений узлов и их координат.
Окончательно для перемещений точек в пределах элемента получим:
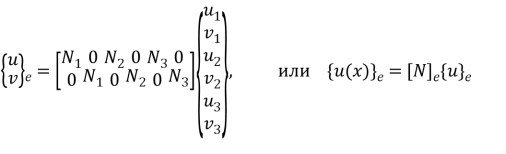 (3.18)
(3.18)
где ![]() — функции формы (линейные по
— функции формы (линейные по ![]() ):
):
![]()
![]() (3.19)
(3.19)
![]()
 (3.20)
(3.20)
где ![]() — площадь треугольного элемента (определитель матрицы).
— площадь треугольного элемента (определитель матрицы).
Используя дифференцирование (1.14), (3.18) и (3.19), получим:
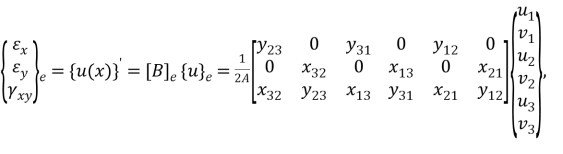 (3.21)
(3.21)
где ![]()
Из (3.21) следует, что деформации постоянны в точках внутри элемента, о чем уже говорилось выше. Следовательно, и напряжения в точках внутри элемента также постоянны. Учитывая эти свойства данного трех узлового элемента, следует ограничить его применение областями, где отсутствует большой градиент напряжений, т. е. вдали от концентраторов напряжений. Этот элемент можно использовать для выполнения предварительных оценочных расчетов.
На основании (3.15) получим выражение для матрицы жесткости треугольного элемента с прямолинейными границами (т. е. с тремя узлами):
![]() (3.22)
(3.22)
где ![]() толщина элемента. Заметим, что в этом уравнении
толщина элемента. Заметим, что в этом уравнении ![]() — симметричная матрица размером
— симметричная матрица размером ![]() .
.
Как видно из уравнений (3.19), для плоского треугольного элемента в глобальной системе координат ![]() функции формы
функции формы ![]() представляют собой достаточно сложные вычисления. Эти выражения существенно упрощаются, если ввести локальную систему координат
представляют собой достаточно сложные вычисления. Эти выражения существенно упрощаются, если ввести локальную систему координат ![]() показано на рис.3.2. Тогда функции формы могут быть записаны существенно проще:
показано на рис.3.2. Тогда функции формы могут быть записаны существенно проще:
![]() (3.23)
(3.23)
Заметим, что:
![]() (3.24)
(3.24)
т.е. условие (3.4 в) выполняется.
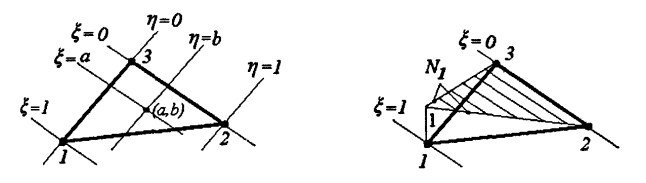
Рис.3.2 Локальная система Рис.3.3 График функций
координат КЭ. формы ![]()
Отметим также, что функции формы (3.23) вдоль каждой из сторон треугольного элемента ведут себя точно так же, как и в одномерном случае (п. 2.1.1): ![]() в узле
в узле ![]() ;
; ![]() во всех остальных узлах и линейно изменяется вдоль стороны элемента. График изменения функции формы
во всех остальных узлах и линейно изменяется вдоль стороны элемента. График изменения функции формы ![]() приведен на рис. 3.3. Функции формы
приведен на рис. 3.3. Функции формы ![]() и
и ![]() ведут себя аналогично.
ведут себя аналогично.
КВАДРАТИЧНЫЙ ТРЕУГОЛЬНЫЙ ЭЛЕМЕНТ
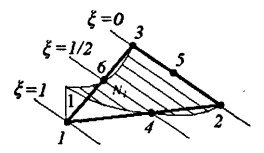
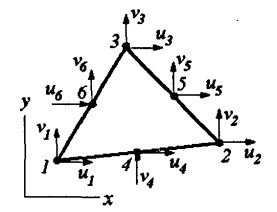 Перейдем к рассмотрению квадратичного треугольного элемента, схема которого показана на рисунке. В отличие от линейного треугольного элемента, элемент данного типа имеет 6 узлов: 3 узла расположены по углам элемента, 3 узла — по середине сторон. Каждый узел, как и в линейном треугольном элементе, имеет 2 степени свободы. В этом случае смещения (
Перейдем к рассмотрению квадратичного треугольного элемента, схема которого показана на рисунке. В отличие от линейного треугольного элемента, элемент данного типа имеет 6 узлов: 3 узла расположены по углам элемента, 3 узла — по середине сторон. Каждый узел, как и в линейном треугольном элементе, имеет 2 степени свободы. В этом случае смещения (![]() ) точек элемента должны выражаться квадратичными функциями их координат
) точек элемента должны выражаться квадратичными функциями их координат
![]()
![]() (3.32)
(3.32)
где ![]() константы.
константы.
Из (3.32) легко вычислить деформации путем дифференцирования:
![]()
![]() (3.33)
(3.33)
![]()
Легко видеть, что в пределах данного элемента деформации являются линейными функциями координат. Таким образом, шести узловой треугольный элемент позволяет более точно описывать поле напряжений и деформаций, чем рассмотренный в предыдущем пункте трех узловой треугольный элемент. В локальной координатной системе ![]() которая полностью совпадает с введенной ранее для линейного треугольного элемента, шесть функций формы для этого элемента можно записать следующим образом:
которая полностью совпадает с введенной ранее для линейного треугольного элемента, шесть функций формы для этого элемента можно записать следующим образом:
![]()
![]()
![]() (3.34)
(3.34)
 Каждая из шести функций формы
Каждая из шести функций формы ![]() в (3.34) является квадратичной функцией локальных координат, но так же, как и в случае линейного трех узлового элемента,
в (3.34) является квадратичной функцией локальных координат, но так же, как и в случае линейного трех узлового элемента, ![]() в узле
в узле ![]() и
и ![]() в остальных узлах (рис.3.5).
в остальных узлах (рис.3.5).
Рис.3.5 График функций
формы ![]()
Используя введенные в (3.34) функции формы, смещения в любой точке элемента можно записать смещения узлов следующим образом:
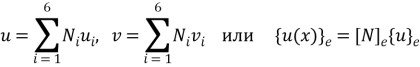
Матрицу жесткости для элемента по-прежнему можно записать в форме
![]() , но здесь
, но здесь ![]() будет иметь квадратичную зависимость от координат
будет иметь квадратичную зависимость от координат ![]() .
.
ЛИНЕЙНЫЙ ЧЕТЫРЕХУГОЛЬНЫЙ ЭЛЕМЕНТ
Линейный четырехугольный элемент, схематично изображенный на рис. 3.6, представляет собой в системе локальных координат ![]() прямоугольник с четырьмя узлами в его вершинах. В системе локальных координат (
прямоугольник с четырьмя узлами в его вершинах. В системе локальных координат (![]() ) функции формы записываются следующим образом:
) функции формы записываются следующим образом:
![]()
![]()
Заметим, что, как и для ранее рассмотренных элементов: ![]()
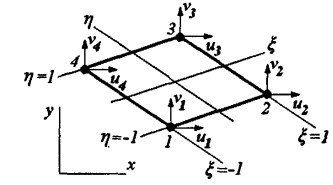
Рис.3.6 Локальная система координат КЭ.
Поле смещений задается следующими уравнениями:
![]() (3.37)
(3.37)
Как следует из (3.37), ![]() и
и ![]() являются билинейными функциями в пределах всего элемента.
являются билинейными функциями в пределах всего элемента.
КВАДРАТИЧНЫЙ ЧЕТЫРЕХУГОЛЬНЫЙ ЭЛЕМЕНТ
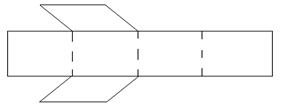
Квадратичный четырехугольный элемент (рис. 3.7) представляет собой прямоугольник с 8 узлами: 4 узла по углам и 4 узла по серединам сторон.
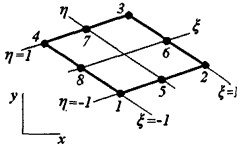
Рис.3.7 Локальная система координат КЭ.
В системе локальных координат 8 функций формы записываются следующим образом:
![]()
. . .
![]()
Заметим, что снова, как и для ранее рассмотренных элементов ![]()
Поле смещений определяется уравнениями:

которые представляют собой квадратичные функции. Деформации и напряжения в точках в пределах четырехугольного 8-узлового элемента являются линейными функциями координат, что позволяет более точно рассчитать напряжения и деформации, чем с помощью 4-узловых элементов.
В заключение отметим, что применение квадратичных треугольных или четырехугольных элементов с шестью или восемью узлами соответственно позволяют моделировать тела с криволинейной границей, что повышает точность результатов моделирования.
3.6. ПРЕОБРАЗОВАНИЕ НАГРУЗКИ
Помимо сил, которые в расчете можно трактовать как сосредоточенные, на элементы конструкции действуют также поверхностные силы (например, внутреннее давление) и объемные силы (например, вес). Как поверхностные, так н объемные силы являются примерами распределенной нагрузки, которая в соответствии с принципами метода конечных элементов не может быть непосредственно приложена к элементу, а должна быть трансформирована к узлам. Приведение распределенной нагрузки к узлам основано на сравнении энергии упругих деформаций. С использованием этого принципа в предыдущих лекциях были сформулированы правила трансформации распределенных нагрузок для одномерных стержневых и балочных элементов.
Рассмотрим правило трансформации поверхностной нагрузки, равномерно распределенной вдоль стороны четырехугольного элемента. Предположим, что
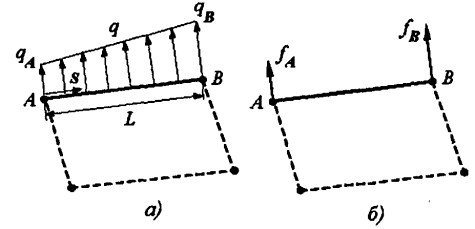
Рис. 3.8 Трансформации поверхностной нагрузки
линейно распределенная поперечная нагрузка q приложена к стороне АВ линейного четырехугольного элемента (рис. 3.8а).
Введя локальную координату S вдоль стороны АВ, запишем выражение для работы ![]() нагрузки q :
нагрузки q :
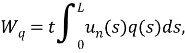
где ![]() — толщина элемента,
— толщина элемента, ![]() длина его стороны, вдоль которой приложена нагрузка
длина его стороны, вдоль которой приложена нагрузка ![]() величина составляющей перемещения, нормальной к стороне АВ приложения нагрузки.
величина составляющей перемещения, нормальной к стороне АВ приложения нагрузки.
Для линейного четырехугольного элемента с учетом (2.5) имеем:
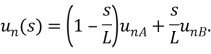
Линейная поперечная нагрузка ![]() также может быть описана аналогичной формулой:
также может быть описана аналогичной формулой:![]()
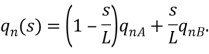
Таким образом, для работы ![]() получим:
получим:
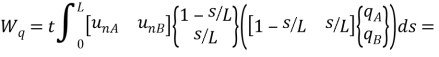
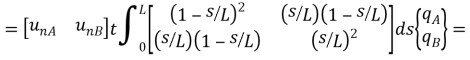
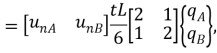
откуда находим вектор эквивалентной нагрузки в узлах (рис 3.8б):
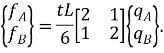
В частном случае, при ![]() , получим:
, получим:
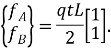
Для квадратичных элементов (треугольных или четырехугольных) с промежуточным узлом посредине стороны распределенная нагрузка перераспре-деляется не по двум узлам, как выше описанном случае, а по трем узлам.
Аналогичным же образом приводится к узлам и распределенная нагрузка, касательная к границе, и объемная нагрузка.
Напряжения в точках элемента вычисляются по следующей формуле:
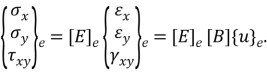
Здесь ![]() — матрица дифференцирования перемещений;
— матрица дифференцирования перемещений; ![]() — вектор смещений узлов, которые должны быть известны для каждого из видов примененных элементов после решения глобальной системы уравнений.
— вектор смещений узлов, которые должны быть известны для каждого из видов примененных элементов после решения глобальной системы уравнений.
Похожие работы
... для каждого симплекс-элемента, а также вектора узловых сил и пермещений. Пользователю имеет возможность задавать характеристики каждого отдельного симплекс-элемента (тетраэдра). Благодаря этому система “плита-грунтовое основание" может быть рассмотрена как неоднородная. Ввод вектора узловых сил осущестляется путем ввода величины силы узлу к которому она прилагается. Вектор перемещений сразу ...
... , необходимых для осуществления проектного решения. СНиП 11-01-95 “Инструкция о порядке разработки, согласования, утверждения и составе проектной документации на строительство предприятий, зданий и сооружений”. Проект состоит из технологической и строительно-экономической частей. Экономическое обоснование технологической части выполняется инженерами-технологами и экономистами-технологами, а ...
... имеют достаточно четкое и правильное представление из собственного жизненного опыта, а формулировки которых являются слишком громоздкими. Выводы по § 1 1. Основные цели изучения темы «Объемы многогранников» в курсе стереометрии – развитие пространственных представлений учащихся, освоение способов вычисления практически важных величин и дальнейшее развитие логического мышления учащихся. ...
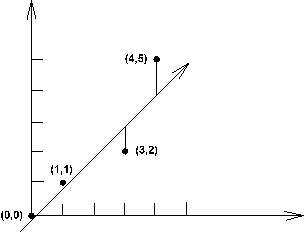
... . Число преобразований не зависит от строчной размерности m, но от m зависит работа, затрачиваемая на выполнение каждого преобразования. глава 3. Использование сингулярного разложения в методе наименьших квадратов При использовании метода сингулярного разложения (SVD – Singular Value Decomposition) мы проводим разложение для матрицы плана. При этом основное уравнение y=Xb приобретает вид y=USVTb ...

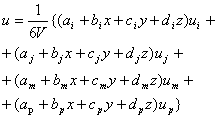


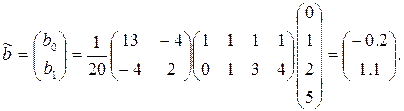

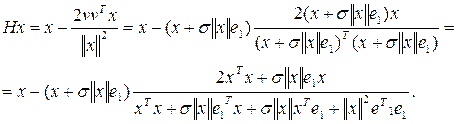
0 комментариев