Навигация
Интерпретация модели (I-компонент теории, interpretation)
6. Интерпретация модели (I-компонент теории, interpretation).
На рис.1 приведены экспериментальные точки и графики функции (16), описывающие дрожжевых клеток в присутствии солей хрома и никеля [13]. При расчете графиков брали значения a, b, р , f, определенные по экспериментальным данным [17]. В пределах точности измерений расчетные кривые согласуются с экспериментом при измененении численности примерно на шесть порядков.
Хорошее согласие теории с экспериментом получено и для других биологических объектов [8, 9]. Поэтому интересно провести верификацию квазихимической модели по характеристикам, связанным с проблемами биологического времени.
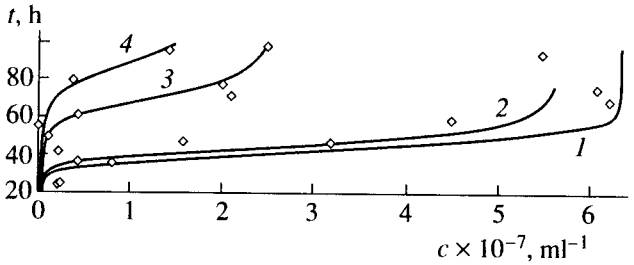
Рис.1. Экспериментальные точки и графики функции (16), описывающие рост пивных дрожжей при разных концентрациях (ммоль/л) солей хрома и никеля [13]: (1) c(Ni) = c(Cr) = 0.0, (2) c(Ni) = 0.5, (3) c(Cr) = 0.5, and (4) c(Ni) + c(Cr) = 0.5 + 0.5. Коэффициенты: a=1.25.10-7 мл/ч, b=0.8ч-1, р=0.32 ч-1, f =2.
Уравнения (12a) можно представить в виде:
| dc1 = Kc1dt, dcm = Kcm dt, | ( 17) |
где величины Kc1=(-px c1+f b cm+w1) и Kcm= (p c1-bx cm-a c1 cm) представляют собой калибровочные коэффициенты для перехода от интервала физического времени dt к интервалам биологического времени dcj.
На основе (17) получают соотношение между конечными временными интервалами:
| D c1 = | ( 17а) |
Калибровочные соотношения (17) обладают следующими свойствами:
1. Коэффициенты Kc1 и Kcm зависят от кинетических констант, характеризующих внутри- и внесистемные взаимодействия. Это определяет специфику биологического времени данного объекта.
2. Коэффициенты Kc1 и Kcm зависят от наблюдаемого состояния объекта, то есть изменяются при движении по фазовой траектории.
3. Коэффициенты Kc1 и Kcm неодинаковы для однотипных элементов данного уровня иерархии. Это означает, что собственное время «течет» с разной скоростью не только на разных уровнях биологической системы, но и в различных элементах одного уровня.
Приращение суммарной массы dmp или численности dNp популяции определяют интервал биологического времени популяции в целом. Для двухстадийной популяции dNp = V(с1+сm), где V – объем системы. Связь между популяционным и физическим временем согласно (17) определяется соотношением:
| dNp = V( Kc1 + Kcm )dt . | ( 18) |
Через длительность клеточного цикла tc в физической шкале (в «детлафах») эта величина выразится в виде:
| dNpd = V( Kc1 + Kcm )dt / tc. | (19) |
Длительность клеточного цикла tc в физической шкале рассчитывают либо по экпериментальным значениям прироста массы или численности клеток, либо по экпериментальным значениям параметров b и p модели (12).
Приращение численности популяции D с12 =c2-c1 в единице обьема наблюдается за время D t12=t2-t1, согласно (16) равное:
| D t12=ln{(c2/c1)[(K1-c1)/(K1-c2)](1+n)}/(npx), | (20) |
где c1, c2 – численности в моменты t1, t2.
Среднее число делений n12 каждой из c1 клеток за это время равно:
| n12= log(c2/c1)/log2 | (21) |
Следователъно, t c можно оценить по формуле:
| tc = D t12/ n12 | (22) |
Другую оценку значения tc можно сделать по кинетическим коэффициентам b и p модели (12):
| tc=1/b +1/p . | (23) |
Расчет по по формулам (22) и (23) для дрожжей S. cerevisae (данные рис.1) дает близкие значения величины tc ( 3,7 и 4,4 ч).
Формула (23) предлагаемой модели клеточной динамики позволяет количественно интерпретировать температурную зависимость длительности клеточного цикла tc , хорошо известную из работ [14-16]. Зависимость коэффициентов b и p от температуры можно аппроксимировать формулой Аррениуса. Тогда согласно (23) температурная зависимость tc выражается в виде:
| t c = b +p = abeEb/T +apeEp/T, | (24) |
где Eb, Ep – энергии активации скоростей деления и роста, ab, ab – соответствующие предэкспоненциальные множители, T – абсолютная температура.
На рис. 2а приведена кривая зависимости tc , рассчитанная по уравнению (24) с помощью эмпирических параметров ab , ab и Eb, Ep. Модельная кривая качественно правильно описывает наблюдаемую закономерность [14- 16].
Подставляя аррениусовские выражения коэффициентов b и p в уравнение (20) получают формулу для расчета зависимости времени роста D t12 популяции до разных ступеней развития (разные c2/c1).
На рис. 2б приведены кривые зависимости D t12 , рассчитанные по уравнению (20) с помощью эмпирических параметров ab , ab и Eb, Ep. Модельные кривые качественно правильно описывают экспериментально наблюдаемые зависимости [14-16].
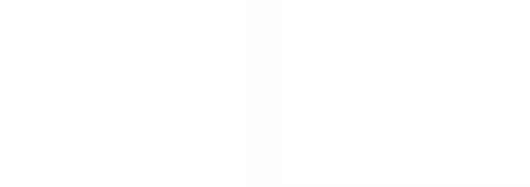
а) б)
Рис. 2. Кривые температурной зависимости длительности развития элементов разных уровней: а) длительность клеточного цикла, рассчитанная по уравнению (24); б) длительности разных стадий развития популяции, рассчитанные по уравнению (20).
Модель (12) дает возможность проверить для популяции применимость функции Бакмана [14]:
| LogH = k log2T, | (25) |
где H – скорость роста популяции, T – время роста, k < 0 –нормировочная постоянная.>
В аналитическом виде функцию Бакмана можно получить, подставляя в (25) выражения H и T, равные, соответственно, правым частям уравнений (14) (при w1 =0) и (16). При этом получают зависимость (25) как явную функцию роста, выражаемого переменной величиной c1 при заданном начальном значении c0. На рис. 4 приведен соответствующий график. Согласно (25), логарифм скорости роста должен быть пропорционален квадрату логарифма времени роста. Однако, как следует из рис. 4, такая зависимость для двухстадийной популяции не наблюдается.
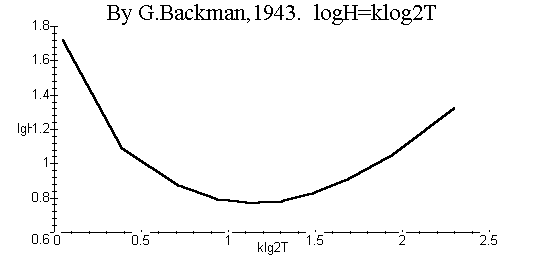
Рис. 3. Функция роста Бакмана (25), построенная на основе двухстадийной модели (16) динамики популяции.
ЛИТЕРАТУРА1. Акчурин И.А. Единство естественнонаучного знания. М., 1974.
2. Левич А.П. // Конструкции времени в естествознании. М., 1996. С. 9-27, 235-288.
3. Шаров А.А. // Конструкции времени в естествознании. М., 1996. С. 96-111.
4. Мейен С.В. // Системность и эволюция. М., 1984. С. 7-32.
5. Ершов Ю.А.// Ж. Физ. химии. 1999. Т.73. № 10, с. 1817 – 1823.
6. Ершов Ю.А.// Ж. Физ. Химии, 2000, т. 74, № 6, с. 1087-1093.
7. Ершов Ю.А. Термодинамика квазиравновесий в биологических системах. М., ВИНИТИ, 1983. 140 с.
8. Гудвин Б. Аналитическая физиология клеток и развивающихся организмов. М.:Мир,1979,288 с.
9. Ершов Ю.А.// Докл. РАН. 1997. Т.72. № 5. с. 627-629.
10. Ершов Ю.А.// Ж. Физ. химии. 1998. Т. 352. № 3. с.553-559.
11. Ершов Ю.А. и др. Кинетика и термодинамика биохимических и физиологических процессов. М., Медицина,1990, 155с.
12. Романовский ю. м., Степанова Н.В., Чернавский Д.С. Математическая биофизика. М. Наука. 1984. - 304 с.
13. Математические проблемы химической кинетики. Сб. Ред. К.И. Замараев, Г.С. Яблонский. Новосибирск: Наука,1989, 335с.
Похожие работы
... и наблюдателя (экперимент М. Стормса) Рисунок 4 3.3. Г.М. Андреева, Н.Н. Богомолова, Л.А. Петровская. Теории диадического взаимодействия (Андреева Г.М., Богомолова Н.Н., Петровская Л.А. Современная социальная психология на Западе (теоретические направления). М.: Изд-во Моск. ун-та, 1978. С. 70-83) Бихевиористская ориентация включает в качестве одного из методологических принципов ...
0 комментариев