Навигация
Лазерные дифракционные измерители
1.5. Лазерные дифракционные измерители
линейных размеров малых объектов
Предположения о возможности использования явления дифракции световых волн для контроля размеров малых объектов были впервые высказаны Роулэндом в 1888 году [13, 14, 15]. Позже он использовал это для качественного контроля изготовления периодической структуры дифракционных решеток. Сущность метода заключалась в том, что, если дифракционную решетку осветить монохроматической световой волной, то на некотором растоянии от нее формируются эквидистантно располо-женные дифракционные максимумы светового потока. При наличии дефек-тов решетки, вокруг этих основных максимумов возникают и добавочные максимумы, которые получили название “духов”. Однако теоретическое обоснование этого явления в то время так и не было сформулировано, что и не позволило определить аналитические зависимости, описывающие функциональную взаимосвязь распределения светового потока в “духах” с дефектами решетки.
Большой вклад в развитие теории дифракционных решеток внес В. Рон-ки, который занимался развитием и совершенствованием их производства более пятидесяти лет, начиная с 1921 года [13, 26]. Он дал простейшую теорию дифракционных решеток, описал их основные свойства и возмож-ность применения для контроля характеристик фотографических объек-тивов.
Г.Харисон [27] в 1949 году предложил способ контроля дифракционных решеток с помощью интерферометра Майкельсона и положил, таким образом, начало разработке схемы интерферометра с дифракционной решеткой для контроля качества самих решеток.
Дифракционные методы контроля качества изготовления периодических структур являются наиболее переспективными. Они положены в основу многочисленных лазерных дифракционных измерителей линейных размеров малых объектов.
Для контроля диаметра тонких отверстий в [28] предложено освещать контролируемые отверстия монохроматической световой волной и измерять амплитуду четных и нечетных максимумов дифракционной картины отверс-тия. Для расширения диапазона диаметра измеряемых отверстий, необхо-димо изменять длину волны ![]() излучения до тех пор, пока амплитуда интерференционного сигнала нечетных гармоник достигнет удвоенного значения амплитуды световой волны в свободном пространстве. Диаметр измеряемого отверстия определяют по формуле :
излучения до тех пор, пока амплитуда интерференционного сигнала нечетных гармоник достигнет удвоенного значения амплитуды световой волны в свободном пространстве. Диаметр измеряемого отверстия определяют по формуле : ![]() , где
, где ![]() - растояние между измеряемым отверстием и точкой измерения светового поля в дифракционной картине. Недостатком метода является необхо-димость применения лазера с перестраиваемой длиной волны генерации.
- растояние между измеряемым отверстием и точкой измерения светового поля в дифракционной картине. Недостатком метода является необхо-димость применения лазера с перестраиваемой длиной волны генерации.
Известны также устройства [29, 30] для допускового контроля геометрических размеров изделий путем соответствующей обработки их дифракционного изображения сложной фотоэлектрической измерительной системой, либо оптической системой пространственной фильтрации. Однако эти устройства являются узко специализированными и требуют предварительного синтеза сложных голографических пространственных фильтров, что позволяет их использовать лишь для качественного допус-кового контроля изделий.
Таким образом лазерные дифрактометры являются наиболее переспек-тивным научным направлением развития автоматизированного метро-логического оборудования. Оно может быть также успешно использовано и для разработки средств автоматизации контроля статистических характе-ристик квазипериодической структуры ЛЗ. Это, в свою очередь, может быть выполнено лишь с созданием специализированных оптических систем обработки изображений (ОСОИ) на базе когерентных оптических спектро-анализаторов (КОС) пространственных сигналов, положенных в основу практически всех известных лазерных дифрактометров.
2. Обзор схем построения лазерных
дифрактометров
Интенсивное развитие этих систем началось в начале 80-х годов. Построение голографических и дифракционных оптических систем для метрологии основано на получении изображений Френеля, либо Фурье исследуемого объекта с последующим анализом их параметров фото-электической измерительной системой.
Основным преимуществом таких метрологических систем, перед ви-зуальными оптическими измерительными приборами, является высокая производительность, что позволяет автоматизировать ряд метрологических процессов в промышленности. Где требуется интегральная комплексная оценка качества изделия.
Для формирования изображений Фурье или Френеля исследуемого объекта используют когерентный оптический спектроанализатор прост-ранственных сигналов, схему построения и геометрические параметры которого выбирают в зависимости от характера решаемой задачи.
В настоящее время уже стала классической схема когерентного оптического спектроанализатора (КОС), приведенная на рис.1.
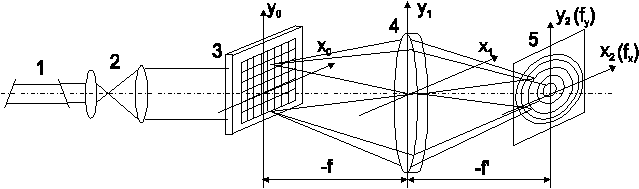
Рис.1. Принципиальная схема когерентного оптического спектро-
анализатора:
1. Лазер;
2. Телескопическая схема Кеплера;
3. Входной транспарант;
4. Фурье-объектив;
5. Дифракционное изображение.
КОС состоит из расположенных последовательно на одной оптической оси источника когерентного излучения - лазера 1 и телескопической систе-мы 2 Кеплера, формирующей плоскую когерентную световую волну. Эта волна падает на входной транспарант 3 с фотографической записью исследуемого сигнала. Входной транспарант 3 расположен в передней фокальной плоскости фурье-объектива 4 (объектива свободного от аберра-ции дисторсии и поперечной сферической ) с фокусным растоянием ![]() . На входном транспаранте 3 световая волна дифрагирует, и фурье-объективом 4 в задней плоскости 5 формируется дифракционное изображение исследуемого сигнала, которое является его фурье-образом и описывается выражением
. На входном транспаранте 3 световая волна дифрагирует, и фурье-объективом 4 в задней плоскости 5 формируется дифракционное изображение исследуемого сигнала, которое является его фурье-образом и описывается выражением
![]() , где А0 -амплитуда плос-кой монохроматической световой волны в плоскости
, где А0 -амплитуда плос-кой монохроматической световой волны в плоскости ![]() ;
; ![]() - длина волны;
- длина волны; ![]() - пространственные частоты, равные
- пространственные частоты, равные ![]() и
и  , где х2, у2 - пространственные координаты в плоскости 5.
, где х2, у2 - пространственные координаты в плоскости 5.
Таким образом, распределение комплексных амплитуд световых полей в задней и передней плоскостях фурье-объектива 4 оптической системы связаны между собой парой преобразований Фурье. Поле в задней фокальной плоскости является пространственным амплитудно-фазовым спектром сигнала, помещенного в его передней фокальной плоскости.
Описанная выше оптическая система выполняет спектральное разложе-ние пространственного сигнала и является когерентным оптическим спектроанализатором. Он позволяет анализировать одновременно ампли-тудный и фазовый спектры как одномерных, так и двумерных пространст-венных сигналов.
Существует две основные разновидности схем построения лазерных дифрактометров. Эти схемы представлены на рис .2 и рис. 3.
При условии фокусировки оптической системы, представленной на рис.2, в ней осуществляется спектральное преобразование Фурье, форми-руемое в плоскости х3у3, над сигналом помещенным во входной плоскости х1у1. Однако, фурье-образ сигнала в такой системе содержит квадратичную модуляцию фазы волны из-за наличия фазового сомножителя, стоящего перед интегралом в выражении :
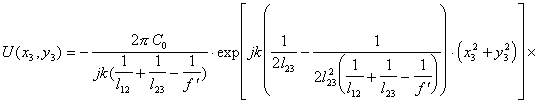
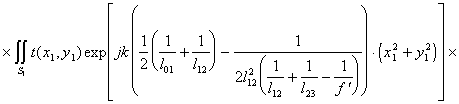
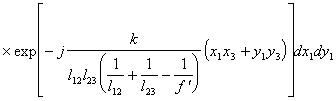 (2.1).
(2.1).
Это выражение описывает пространственное распределение комплекс-ных амплитуд светового поля в плоскости х3у3 спектрального анализа и со-держит ряд взаимонезависимых квадратичных фазовых сомножителей.
Наличие фазовой модуляции фурье-образа приводит к тому, что при ре-гистрации его методами голографии в результирующей интерферограмме возникают дополнительные аберрации, значительно влияющие на его ка-чество. Эта фазовая модуляция также имеет важное значение и не может быть опущена в случае дальнейших преобразований деталями оптической системы фурье-образа сигнала. Но эта модуляция может быть устранена при соответствующем выборе геометрических параметров оптической системы, т.е.
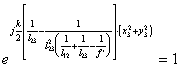 , при
, при  . (2.2).
. (2.2).
Таким образом, квадратическая фазовая модуляция фурье-образа устра-нима лишь в двух случаях:
при размещении сигнального транспаранта в передней фокальной плоскости фурье-объектива, что полностью совпадает с полученными ранее результатами исследований, но лишь для КОС с плоской вол-ной во входной плоскости, т.е. при  .
.
при ![]() , т.е. плоскость х3у3 спектрального анализа должна совпа-дать с плоскостью х2у2 размещения фурье-объектива, что физически нереализуемо в оптической системе, согласно условию Гауса.
, т.е. плоскость х3у3 спектрального анализа должна совпа-дать с плоскостью х2у2 размещения фурье-объектива, что физически нереализуемо в оптической системе, согласно условию Гауса.
Учитывая выражения 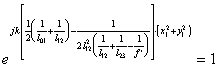 и (2.2) можем преобразовать (2.1) к виду:
и (2.2) можем преобразовать (2.1) к виду:
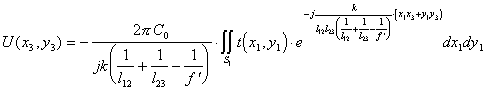 (2.3),
(2.3),
откуда видно, что квадратичные фазовые искажения фурье-образа сигнала устранимы не только при освещении входного транспаранта плоской, но и сферической волной.
При условии фокусировки оптической системы, показанной на рис.3, в ней осуществляется спектральное преобразование Фурье, формируемое в плоскости х3у3, над пространственным сигналом, помещенном в плоскости х2у2. Однако, фурье-образ сигнала в такой системе содержит квадра-тическую модуляцию фазы волны из-за наличия фазового сомножителя. Наличие фазовой модуляции фурье-образа сигнала приводит к допол-нительным аберрациям интерферограммы при регистрации методами голографии. Эта модуляция имеет также важное значение и не может быть опущена. Модуляция может быть устранена на оптической оси системы и при ![]() , т.е. при фокусировке оптической системы на бесконечность. Но в этом случае оптическая система не будет осуществлять спектральное преобразование Фурье.
, т.е. при фокусировке оптической системы на бесконечность. Но в этом случае оптическая система не будет осуществлять спектральное преобразование Фурье.
Для оптической системы КОС, представленной на рис.3, квадратичные фазовые искажения, приводящие к аберрационным искажениям фурье-об-раза сигнала, не могут быть устранены лишь путем соответствующего выбора геометрических парметров оптической системы. Для устранения этих искажений необходимо оптическую систему дополнить корректирую-щим фильтром с фазовой характеристикой, сопряженной к квадратичным фазовым искажениям фурье-образа сигнала.
Итак можно сделать выводы:
Квадратичные фазовые искажения фурье-образа сигнала устранимы путем соответствующего выбора геометрических размеров оптичес-кой системы, но лишь для КОС, выполненного по схеме “входной транспарант - перед фурье-объективом”.
При расположении ЛЗ в передней фокальной плоскости фурье-объектива масштаб ее дифракционного изображения не зависит от радиуса освещающей волны, а определяется величиной фокусного растояния и длиной волны излучения лазера. Это позволяет рас-ширить дифракционную полосу анализа путем увеличения радиуса освещающей волны, не изменяя, при этом масштаб дифракционного изображения.
При освещении ЛЗ, расположенной в передней фокальной плоскости фурье-объектива, плоской световой волной, погрешность прост-ранственной частоты зависит лишь от длины волны излучения лазера и фокусного растояния фурье-объектива, что позволяет обеспечить ее уменшение путем увеличения ![]() и
и ![]() .
.
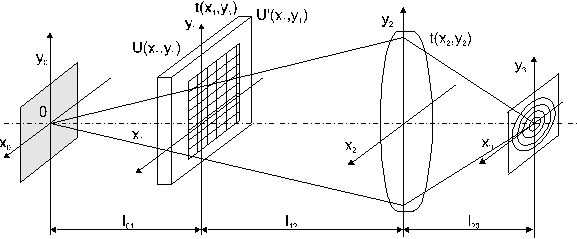
Рис.2. Схема КОС со входным транспарантом перед фурье-объективом
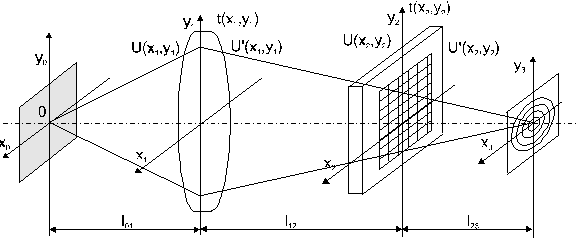
Рис.3. Схема КОС со входным транспарантом за фурье-объективом
3.Математическая модель квазипериодической
структуры СВЧ линий замедления
При статистических исследованиях геометрических размеров элементов пространственной структуры ЛЗ установлено, что из-за различных техноло-гических погрешностей, эти размеры являются величинами случайными с нормальным законом распределения. Таким образом, пространственная структура ЛЗ не является строго переодической, а поэтому ее энер-гетический спектр будет отличаться от энергетического спектра периоди-ческих структур.
Из скалярной теории [7, 8] известно, что оптической системой КОС в плоскости спектрального анализа формируется дифракционное изображе-ние пространственного объекта, помещенного во входной плоскости. Математические зависимости, описывающие форму дифракционного изоб-ражения, могут быть определены лишь путем решения задачи о дифракции когерентной световой волны на пространственной структуре объекта. Одна-ко для пространственной структуры ЛЗ с флуктуациями периодичности, решение такой задачи чисто оптическими методами не может быть полу-чено из-за значительной математической сложности ее. Кроме, того эти методы применимы лишь для решения дифракционных задач на регу-лярных детерминированных пространственных структурах и неприменимы для случайных пространственных сигналов.
Поэтому в настоящее время такие задачи для случайных оптических сигналов решают в оптике с применением методов статистической радио-физики в силу единства физических процессов и математических методов анализа прохождения электрических сигналов в электрических цепях и распостранения пространственных сигналов в оптических системах. Это позволяет определить распределение освещенности в дифракционном изображении квазипериодической пространственной структуры ЛЗ (т.е. ее энергетический спектр) путем вычисления усредненного квадрата преобра-зования Фурье над ее амплитудным коэфициентом пропускания.
Пространственная штриховая структура ЛЗ является квазипериодичес-ким сигналом, в технике ОСОИ, и состоит из взаимонезависимых прозрач-ных щелей и непрозрачных стенок. К тому же период пространственной структуры ЛЗ также является случайной величиной, так как он равен сумме двух взаимонезависимых величин. Таким образом, пространственная струк-тура ЛЗ относится к классу случайных квазипериодических сигналов.
Поскольку освещенность пространственной структуры ЛЗ, помещенной во входной плоскости КОС, равномерна по полю, то ее амплитудный коэфициент попускания ![]() может быть описан единично-нулевой функ-
может быть описан единично-нулевой функ-
цией. Поэтому, в пределах ширины ![]() прозрачных щелей функция
прозрачных щелей функция ![]() , а в пределах ширины
, а в пределах ширины ![]() непрозрачных стенок, соответственно, 0. Кроме того, ширина щелей
непрозрачных стенок, соответственно, 0. Кроме того, ширина щелей ![]() и стенок
и стенок ![]() являются величинами взаимонезави-симыми, поскольку при изгибах стенок толщина
являются величинами взаимонезави-симыми, поскольку при изгибах стенок толщина ![]() их не изменяется, а изменяется лишь ширина
их не изменяется, а изменяется лишь ширина ![]() щелей. Взаимонезависимость этих величин также возникает и потому, что зубья в верхней и нижней гребенках наре-заются раздельно на разных заготовках, после спаивания которых обра-зуются между зубьями щели, а ширина их уже не зависит от толщины зубьев, что подтверждается также малостью коэфициента корреляции
щелей. Взаимонезависимость этих величин также возникает и потому, что зубья в верхней и нижней гребенках наре-заются раздельно на разных заготовках, после спаивания которых обра-зуются между зубьями щели, а ширина их уже не зависит от толщины зубьев, что подтверждается также малостью коэфициента корреляции ![]() для размеров
для размеров ![]() и
и ![]() .
.
Фрагмент квазипериодической пространственной структуры ЛЗ и соот-ветствующая ему функция пропускания ![]() в сечении у=0 показаны на рис.4 (а и б), где Рх - период пространственной структуры, равный
в сечении у=0 показаны на рис.4 (а и б), где Рх - период пространственной структуры, равный ![]() .
.
Поскольку ширина ![]() щелей и
щелей и ![]() стенок являются величинами случайны-ми и взаимонезависимыми, то и период
стенок являются величинами случайны-ми и взаимонезависимыми, то и период ![]() пространственной структуры ЛЗ будет также величиной случайной. Период
пространственной структуры ЛЗ будет также величиной случайной. Период ![]() является суммой двух случай-ных величин с нормальными законами распределения, следовательно, закон распределения
является суммой двух случай-ных величин с нормальными законами распределения, следовательно, закон распределения ![]() также будет нормальным.
также будет нормальным.
Таким образом, амплитудный коэфициент пропускания ![]() прост-ранственной квазипериодической структуры ЛЗ может быть описан функ-цией вида
прост-ранственной квазипериодической структуры ЛЗ может быть описан функ-цией вида
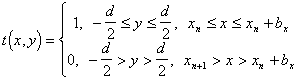 (2.4), где
(2.4), где ![]() - порядковый номер щели,
- порядковый номер щели, ![]() - пространственная координата положения начала щели,
- пространственная координата положения начала щели, ![]() - высота перекрытия зубьев в квазипериодической структуре ЛЗ.
- высота перекрытия зубьев в квазипериодической структуре ЛЗ.
Из выражения (2.4) видно, что переменные х и у функции ![]() взаимо-независимы, а поэтому эта функция является функцией с разделяемыми переменными, и может быть представлена в виде произведения функций
взаимо-независимы, а поэтому эта функция является функцией с разделяемыми переменными, и может быть представлена в виде произведения функций ![]() и
и ![]() , т.е.
, т.е. ![]() (2.5).
(2.5).
В выражении (2.5) функция ![]() является финитной в пределах высо-ты
является финитной в пределах высо-ты ![]() перекрытия зубьев верхней и нижней гребенок пространственной структуры ЛЗ вдоль координаты х, как показано на рис.4б.
перекрытия зубьев верхней и нижней гребенок пространственной структуры ЛЗ вдоль координаты х, как показано на рис.4б.
Для оптической системы КОС пространственная структура ЛЗ является квазипериодическим сигналом. В свою очередь, основными характеристи-ками такого сигнала, т.е. пространственной структуры ЛЗ, являются:
средние размеры ![]() и
и ![]() ширины стенок и щелей, а также средние квадратические отклонения СКО
ширины стенок и щелей, а также средние квадратические отклонения СКО ![]() и
и ![]() от них соответственно;
от них соответственно;
законы распределения ![]() и
и ![]() размеров стенок и щелей;
размеров стенок и щелей;
спектральная и корреляционная функции.
Для описания спектральных и корреляционных функций случайных сигналов часто используются характеристические функции. Характеристи-ческая функция ![]() случайной величины
случайной величины ![]() является фурье-образом ее закона распределения
является фурье-образом ее закона распределения ![]() , т.е.
, т.е. 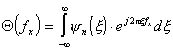 , где
, где ![]() - простран-ственная частота, измеряемая в [мм-1], поскольку в рассматриваемом случае координата
- простран-ственная частота, измеряемая в [мм-1], поскольку в рассматриваемом случае координата ![]() является пространственной и имеет размерность [мм].
является пространственной и имеет размерность [мм].
Тогда с учетом 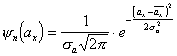 получим:
получим:
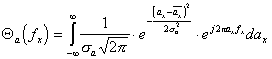 , а вводя замену переменных вида
, а вводя замену переменных вида
![]() . Этот интеграл в новых пределах интегрирования от
. Этот интеграл в новых пределах интегрирования от  до
до ![]() можно представить через элементарные функции следующим выражением
можно представить через элементарные функции следующим выражением
![]() (2.6) , и аналогично
(2.6) , и аналогично  (2.7).
(2.7).
Полученные выражения (2.6) и (2.7) являются характеристическими функциями квазипериодической пространственной структуры ЛЗ с нормаль-ным законом распределения ширины ![]() стенок и
стенок и ![]() щелей.
щелей.
Как в оптических, так и в электронных устройствах спектрального анали-за сигналов, существует возможность получения как амплитудного, так и энергетического их спектров. Однако в теории спектрального анализа пространственных сигналов известно, что при использовании квадратичес-ких фотодетекторов для регистрации параметров дифракционного изобра-жения, формируемого оптической системой КОС, автоматически на ее вы-ходе формируется энергетический спектр исследуемого сигнала. Парамет-ры такого спектра могут быть измерены соответствующими контрольно-измерительными приборами, а форма его определена с применением мето-дов статистической радиооптики путем интегрального преобразования Винера-Хинчина, либо на основе теоремы Хилли.
Поэтому используя аналогию математических методов исследования спектральных характеристик пространственных и временных сигналов, распределение комплексных амплитуд спектра пропускания ![]() в дифракционном изображении пространственной квазипериодической струк-туры ЛЗ, можно определить как
в дифракционном изображении пространственной квазипериодической струк-туры ЛЗ, можно определить как  , или с уче-том (2.5)
, или с уче-том (2.5) ![]() .
.
Полученное выражение описывает амплитудный спектр функции ![]() пропускания квазипериодической пространственной структуры ЛЗ. Энерге-тический спектр
пропускания квазипериодической пространственной структуры ЛЗ. Энерге-тический спектр  этой функции может быть определен с помощью теоремы Хилли [3.11] как
этой функции может быть определен с помощью теоремы Хилли [3.11] как  , или же
, или же
![]() .
.
Однако в работах [16, 17] показано, что для квазипериодического сигнала, описываемого единично-нулевой функцией вида (2.4)
![]() (2.8), где
(2.8), где  - дискретная составляющая спектра на нулевой частоте, которая для квазипериодической структуры ЛЗ будет равна
- дискретная составляющая спектра на нулевой частоте, которая для квазипериодической структуры ЛЗ будет равна
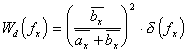 (2.9) , а
(2.9) , а  - непрерывная составляющая спектра, равная:
- непрерывная составляющая спектра, равная:  (2.10), что справедливо для
(2.10), что справедливо для ![]() и
и  не равных 1, согласно [3.35].
не равных 1, согласно [3.35].
В выражениях (2.9) и (2.10) параметр ![]() является пространственной частотой энергетического спектра исследуемого сигнала, величина которой определяется коэфициентом
является пространственной частотой энергетического спектра исследуемого сигнала, величина которой определяется коэфициентом ![]() масштаба и зависит от схемы построения и геометрических размеров оптической системы КОС.
масштаба и зависит от схемы построения и геометрических размеров оптической системы КОС.
Для определения формы энергетического спектра пространственной структуры ЛЗ рассмотрим вещественную часть комплексной дроби в выражении (2.10), обозначив ее через В, т.е.
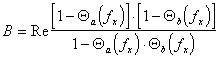 (2.11). Подставив в (2.11) выражения (2.6) и (2.7) характеристических функций
(2.11). Подставив в (2.11) выражения (2.6) и (2.7) характеристических функций ![]() и
и  получим:
получим:
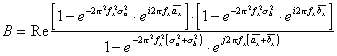 (2.12).
(2.12).
Выражение (2.12) представляет собой комплексную дробь вида  , вещественная часть которой равна
, вещественная часть которой равна  (2.13).
(2.13).
Тогда, выполнив алгебраические преобразования над (2.12) с использо-ванием (2.13), вещественную часть В выражения (2.12) можно представить в виде :
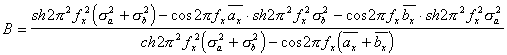 (2.14).
(2.14).
Подставив (2.14) в (2.10), получим уравнение непрерывной составляю-щей энергетического спектра квазипериодической пространственной струк-туры ЛЗ:
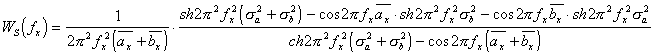 (2.15), а энергетический спектр пространственной структуры ЛЗ с нормаль-ным законом распределения ширины щелей и стенок может быть представ-лен следующим выражением:
(2.15), а энергетический спектр пространственной структуры ЛЗ с нормаль-ным законом распределения ширины щелей и стенок может быть представ-лен следующим выражением:
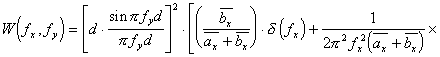
![]()
 (2.16).
(2.16).
Наибольший интерес для практической реализации в оптических системах КОС для автоматизации контроля статистических характеристик пространственной структуры ЛЗ представляет второе слагаемое выражения (2.16), содержащее функциональную взаимосвязь этих характеристик. Пос-кольку это слагаемое содержит гармонические функции, что указывает на наличие частот ![]() экстремальных амплитуд спектра. Величины экстремаль-ных амплитуд спектра и их частоты
экстремальных амплитуд спектра. Величины экстремаль-ных амплитуд спектра и их частоты ![]() полностью определяются статисти-ческими характеристиками геометрических размеров элементов простран-ственной структуры ЛЗ.
полностью определяются статисти-ческими характеристиками геометрических размеров элементов простран-ственной структуры ЛЗ.
Первое слагаемое в (2.16) описывает амплитуду спектра на нулевой частоте, а в оптической системе КОС - интенсивность недифрагированного светового потока, который фокусируется оптической системой на его оси в плоскости спектрального анализа.
Похожие работы
... мере, синергетическим стилем мышления может быть некой платформой для открытого творческого диалога между учеными, мыслителями, деятелями искусства, имеющими различные творческие установки и взгляды на мир. 2. Некоторые парадоксальные следствия синергетики Множество новых парадоксальных идей, образов и представлений возникает в синергетике. Кроме того, с точки зрения синергетики может быть ...
0 комментариев