Навигация
Задание характеристик элементов измерительной
4. Задание характеристик элементов измерительной
системы
Источник излучения газовый He-Ne лазер ЛГН-207А:
Диаметр пучка на растоянии 40 мм от переднего зеркала резонатора 0.52 мм.
Длина волны излучения 0.6328 мкм.
Расходимость излучения 1.85 мрад.
Мощность 2 мВт.
Характеристики оптичесих элементов:
Длина линии задержки 15 мм.
Высота линии зажержки 4 мм.
Диаметр фурье-объектива 24 мм.
Фокусное растояние фурье-объектива 104.98 мм.
Характеристики приемника излучения:
ПЗС-матрица, производстведена в Японии.
Количество элементов 512х340.
Размер чувствительной прощадки одного элемента 20х20 мкм.
Спектральная чувствительность 0.4 B/Вт.
Пороговый поток 10-12 Вт.
5. Математическая модель измерительной
системы
Оптическая система КОС, выполненная по схеме “входной транспарант перед фурье-объективом”, состоит из ряда последовательно расположен-ных вдоль оптической оси узлов: источник когерентного излучения, входной транспарант, фурье-объектив, фоторегистратор спектра (рис.2).
В такой системе, для получения высококонтрастного и сфокусирован-ного изображения исследуемого сигнала, источником когерентного излу-чения является точечный источник, излучаемое поле которого описывается функцией:  (5.1), где А0-амплитуда световой волны источника;
(5.1), где А0-амплитуда световой волны источника; ![]() - дельта-функция Дирака. Кроме того, в оптике принято считать источник точечным, если его размеры в десять и более раз меньше растояния до оптической системы, что обычно всегда имеет место на практике для КОС.
- дельта-функция Дирака. Кроме того, в оптике принято считать источник точечным, если его размеры в десять и более раз меньше растояния до оптической системы, что обычно всегда имеет место на практике для КОС.
Тогда, распределение поля ![]() в плоскости х1у1 согласно принципу Гюйгенса-Френеля, будет описываться выражением :
в плоскости х1у1 согласно принципу Гюйгенса-Френеля, будет описываться выражением :
![]() (5.3), где
(5.3), где ![]() - оператор преобразования Френеля ; СФ- комплексная постоянная, равная
- оператор преобразования Френеля ; СФ- комплексная постоянная, равная  . Если в плоскости х1у1 помещен пространственный транспарант с амплитудным коэфициентом пропускания
. Если в плоскости х1у1 помещен пространственный транспарант с амплитудным коэфициентом пропускания  , являюшийся записью исследуемого сигнала, то распределение поля за транспарантом может быть описано как
, являюшийся записью исследуемого сигнала, то распределение поля за транспарантом может быть описано как
![]() (5.2).
(5.2).
Применив принцип Гюйгенса-Френеля (5.3), можно определить распре-деление светового поля в плоскости х2у2 перед фурье-объективом, а поле за ним - применив (5.2).
Таким образом, распределение поля в плоскости х3у3 анализа будет описываться :
![]() (5.4), где
(5.4), где ![]() - оператор Френеля для преобразования поля на i-м участке свободного пространства толщиной li.
- оператор Френеля для преобразования поля на i-м участке свободного пространства толщиной li.
Рассмотрим последовательно распостранение когерентной световой волны в оптической системе КОС, представленной на рис. 2.
Подставив (5.1) в (5.3), определим распределение светового поля во входной плоскости х1у1 перед транспарантом 
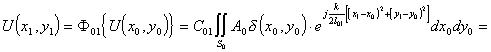
![]() , где
, где  (5.5).
(5.5).
Выражение (5.5) получено с использованием фильтрующего свойства дельта-функции и описывает расходящуюся сферическую волну в плоскости х1у1 перед входным транспарантом в параксиальном приближении. Исполь-зование фильтрирующего свойства ![]() -функции допустимо в силу прост-ранственной инвариантности рассматриваемой параксиальной области оптической системы. Такое допущение обычно всегда имеет место на прак-тике, поскольку для уменшения влияния аберраций оптической системы на качество фурье-образа, используют лишь ее центральную часть - парак-сиальную область.
-функции допустимо в силу прост-ранственной инвариантности рассматриваемой параксиальной области оптической системы. Такое допущение обычно всегда имеет место на прак-тике, поскольку для уменшения влияния аберраций оптической системы на качество фурье-образа, используют лишь ее центральную часть - парак-сиальную область.
Определив распределение поля за входным транспарантом  c ис-пользованием (5.2), поле во входной плоскости фурье-объектива, согласно принципу Гюйгенса-Френеля, можно представить как
c ис-пользованием (5.2), поле во входной плоскости фурье-объектива, согласно принципу Гюйгенса-Френеля, можно представить как
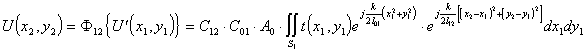 (5.6), где
(5.6), где  - постоянный фазовый коэфициент Френеля; S1 -область интегрирования по аппертуре входного транспаранта.
- постоянный фазовый коэфициент Френеля; S1 -область интегрирования по аппертуре входного транспаранта.
Распределение поля в плоскости х2у2 за фурье-объективом, согласно (5.2) будет
![]() (5.7), а подставив (5.6) в (5.7) с учетом (5.3), распределение поля в плоскости х3у3 анализа можно представить в виде :
(5.7), а подставив (5.6) в (5.7) с учетом (5.3), распределение поля в плоскости х3у3 анализа можно представить в виде :
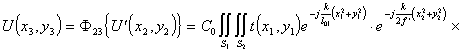
![]() (5.7),
(5.7),
где ![]() (5.8).
(5.8).
Поскольку переменные х1, у1 и х2, у2 интегрирования, в полученном выражении (5.7), являются величинами взаимонезависимыми, то их можно поменять местами, а (5.7) примет вид:
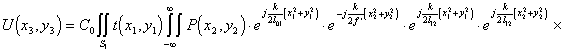
![]() (5.9),
(5.9),
где ![]() (5.10), а
(5.10), а  - функция зрачка фурье-объектива, удовлетворяющая условиям (5.10) финитности в области
- функция зрачка фурье-объектива, удовлетворяющая условиям (5.10) финитности в области ![]() .
.
Для анализа выражения (5.9), рассмотрим отдельно внутренний интег-рал, который описывает суперпозицию светового поля по входной аперту-ре ![]() фурье-объектива и группируя совместно одинаковые экспотенциаль-ные сомножители, упростим его. Формальное увеличение пределов интег-рирования по входной апертуре
фурье-объектива и группируя совместно одинаковые экспотенциаль-ные сомножители, упростим его. Формальное увеличение пределов интег-рирования по входной апертуре ![]() фурье-объектива до бесконечности возможно, поскольку размеры входного транспаранта
фурье-объектива до бесконечности возможно, поскольку размеры входного транспаранта  всегда на мно-го меньше аппертуры
всегда на мно-го меньше аппертуры ![]() фурье-объектива, а также чем требуется по усло-виям параксиальности Френеля и условию (5.10) финитности функции зрачка фурье-объектива. Поэтому дифракционное изображение сигнала
фурье-объектива, а также чем требуется по усло-виям параксиальности Френеля и условию (5.10) финитности функции зрачка фурье-объектива. Поэтому дифракционное изображение сигнала  в плоскости х3у3 анализа ограничено не апертурой
в плоскости х3у3 анализа ограничено не апертурой ![]() фурье-объек-тива, а апертурой
фурье-объек-тива, а апертурой ![]() входного транспаранта. Это влияние уменшается, чем ближе расположен входной транспарант к фурье-объективу, т.е. чем меньше растояние
входного транспаранта. Это влияние уменшается, чем ближе расположен входной транспарант к фурье-объективу, т.е. чем меньше растояние ![]() , что обычно всегда выполняется на практике. Учитывая это можно записать
, что обычно всегда выполняется на практике. Учитывая это можно записать  в пределах области интегрирова-ния
в пределах области интегрирова-ния
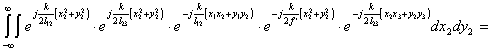
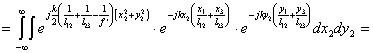
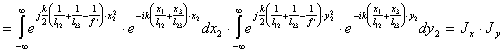 (5.11).
(5.11).
Выражение (5.11) содержит два взаимонезависимых подобных интегра-ла ![]() и
и ![]() , каждый из которых может быть вычислен с использованием табличного интеграла вида :
, каждый из которых может быть вычислен с использованием табличного интеграла вида :
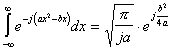 (5.12). Применив (5.12) к (5.11), но предва-рительно обозначив через
(5.12). Применив (5.12) к (5.11), но предва-рительно обозначив через
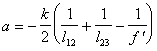 ,
,  и
и 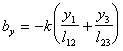 (5.12), выражение (5.11) можно представить в виде :
(5.12), выражение (5.11) можно представить в виде :
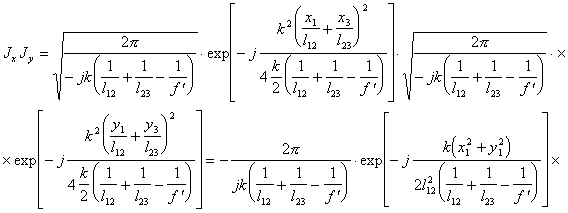
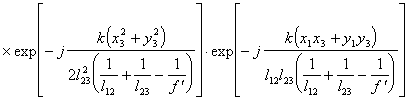 (5.13).
(5.13).
Подставив (5.13) в (5.9) получим
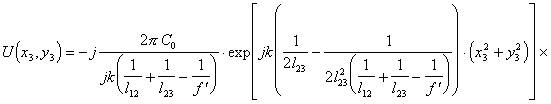
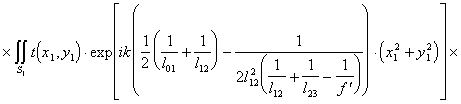
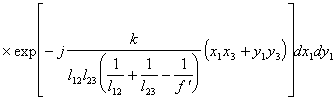 (5.14).
(5.14).
Выражение (5.14) описывает пространственное распределение комп-лексных амплитуд светового поля в плоскости х3у3 спектрального анализа и содержит ряд взаимонезависимых квадратичных фазовых сомножителя, по-ле в плоскости х3у3 является фурье-образом поля в плоскости х1у1 за входным транспарантом  с пространственными частотами
с пространственными частотами ![]() и
и ![]() , равными
, равными 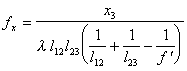 , и
, и  (5.15)
(5.15)
Подинтегральный квадратичный сомножитель в выражении (5.14) для распределения поля в плоскости х3у3 анализа
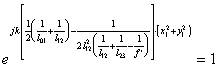 (5.16), при
(5.16), при
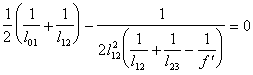 (5.17)
(5.17)
Решив уравнение (5.17) относительно ![]() определим
определим
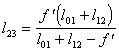 (5.18).
(5.18).
Полученное уравнение (5.18) представляет собой известное условие Гауса о фокусировке оптической системы, согласно
![]() (5.19)
(5.19)
Таким образом, только при условии фокусировки оптической системы, представленной на рис.2, в ней осуществляется спектральное преобразо-вание Фурье, формируемое в плоскости х3у3, над сигналом  , поме-щенным во входной плоскости х1у1. Однако, фурье-образ сигнала содержит квадратичную модуляцию фазы волны из-за наличия фазового сомно-жителя, стоящего перед интегралом в выражении (5.14). Наличие фазовой модуляции фурье-образа приводит к тому, что при регистрации его методами голографии в результирующей интерферограмме возникают дополнительные аберрации, значительно влияющие на его качество. Эта модуляция также имеет важное значение и не может быть опущена в случае дальнейших преобразований деталями оптической системы фурье-образа
, поме-щенным во входной плоскости х1у1. Однако, фурье-образ сигнала содержит квадратичную модуляцию фазы волны из-за наличия фазового сомно-жителя, стоящего перед интегралом в выражении (5.14). Наличие фазовой модуляции фурье-образа приводит к тому, что при регистрации его методами голографии в результирующей интерферограмме возникают дополнительные аберрации, значительно влияющие на его качество. Эта модуляция также имеет важное значение и не может быть опущена в случае дальнейших преобразований деталями оптической системы фурье-образа ![]() сигнала
сигнала  . Однако, квадратичная модуляция фазы фурье-образа может быть устранена при соответствующем выборе геометри-ческих параметров оптической системы, т.е.
. Однако, квадратичная модуляция фазы фурье-образа может быть устранена при соответствующем выборе геометри-ческих параметров оптической системы, т.е.
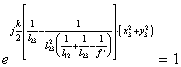 (5.20) при
(5.20) при  (5.21).
(5.21).
Решив уравнение (5.21) относительно ![]() находим
находим
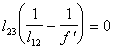 (5.22) при
(5.22) при ![]() =0, либо
=0, либо ![]() .
.
Таким образом, квадратическая фазовая модуляция фурье-образа устра-нима лишь в двух случаях:
при размещении сигнального транспаранта в передней фокальной плоскости фурье-объектива, что полностью совпадает с полученными ранее результатами исследований, но лишь для КОС с плоской вол-ной во входной плоскости, т.е. при  .
.
при ![]() , т.е. плоскость х3у3 спектрального анализа должна совпа-дать с плоскостью х2у2 размещения фурье-объектива, что физически нереализуемо в оптической системе, согласно условию Гауса.
, т.е. плоскость х3у3 спектрального анализа должна совпа-дать с плоскостью х2у2 размещения фурье-объектива, что физически нереализуемо в оптической системе, согласно условию Гауса.
Учитывая (5.16) и (5.20) выражение (5.14) можно представить в виде:
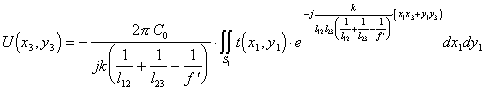 (5.23),
(5.23),
откуда видно, что квадратичные фазовые искажения фурье-образа (5.14) сигнала устранимы не только при освещении входного транспаранта плос-кой, но и сферической волной при выполнении условий (5.18 ) и (5.22).
Выходной электрический сигнал ФИС представляет собой решение известной в оптике задачи о набегании светового пятна, распределение освещенности в котором описывается выражением:
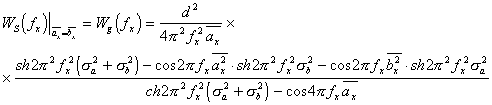 , на узкую щеле-вую диафрагму вдоль координаты х3. Наиболее общим методом решения подобных задач является вычисление интеграла свертки функции освещенности с функцией
, на узкую щеле-вую диафрагму вдоль координаты х3. Наиболее общим методом решения подобных задач является вычисление интеграла свертки функции освещенности с функцией ![]() пропускания полевой диафрагмы ФИС, равной:
пропускания полевой диафрагмы ФИС, равной:
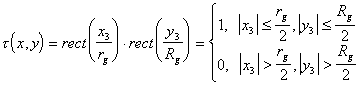 (5.24), где
(5.24), где ![]() - ширина щели вдоль координаты х3,
- ширина щели вдоль координаты х3, ![]() - высота щели вдоль координаты у3.
- высота щели вдоль координаты у3.
Распределение ![]() комплексных амплитуд
световой волны в плос-
комплексных амплитуд
световой волны в плос-
кости х3у3 анализа КОС описывается выражением (5.23) и является прост-ранственно-частотным фурье-образом входного сигнала ![]() т.е.
т.е.
![]() .
.
Из уравнений Максвелла для электромагнитной волны следует, что энергия преносимая волной, пропорциональна квадрату амплитуды напря-женности электромагнитного поля, т.е.
![]() (5.25), где К - постоянный коэфициент, зависящий от свойств среды, где распостраняется электромагнитная волна [14, 23]. Поэтому пространственно-частотный энергетический спектр
(5.25), где К - постоянный коэфициент, зависящий от свойств среды, где распостраняется электромагнитная волна [14, 23]. Поэтому пространственно-частотный энергетический спектр ![]() входного сигнала
входного сигнала  пропорционален распределению освещенности
пропорционален распределению освещенности  в плоскости спектрального анализа КОС, т.е.
в плоскости спектрального анализа КОС, т.е.
![]() (5.26), где
(5.26), где  ,
,
![]() - взаимосвязь между пространственными х(у) и пространственно-частотными
- взаимосвязь между пространственными х(у) и пространственно-частотными ![]() координатами в плоскости спектрального анализа КОС;
координатами в плоскости спектрального анализа КОС; ![]() комплексная постоянная, определяемая (5.8).
комплексная постоянная, определяемая (5.8).
Тогда согласно [11, 12] выходной сигнал ФИС с безинерционным фотоприемником, воспринимающим весь световой поток, прошедший через полевую диафрагму, можно определить как
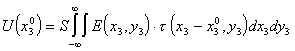 (5.27), где
(5.27), где ![]() - интегральная чувствитель-ность фотоприемника;
- интегральная чувствитель-ность фотоприемника; ![]() - положение центра полевой диафрагмы в фиксированный момент времени при измерении сечения спектра
- положение центра полевой диафрагмы в фиксированный момент времени при измерении сечения спектра  вдоль координаты
вдоль координаты ![]() .
.
Так как в общем виде интеграл свертки (5.27) вычисляется аналитически лишь для простых элементарных функций, то при вычислении свертки сложных монотонно-гладких функций, значительно отличающихся по шири-не, допускают аппроксимацию результата более широкой функцией, что обеспечивает погрешность не более 6-10% в пределах более широкой функции [10, 17, 18].
Поэтому для повышения точности измерения спектра и упрощения вычисления интеграла (5.27), ширина полевой диафрагмы ![]() выбрана равной 20 мкм, что в десятки раз меньше ширины максиумов функции
выбрана равной 20 мкм, что в десятки раз меньше ширины максиумов функции  .
.
Применительно к рассматриваемому случаю выражение (5.27) с учетом (2.16) и (5.24) может быть представлено в виде
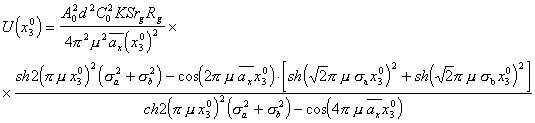 (5.28).
(5.28).
Полученное выражение (5.28) описывает форму электрического сигнала на выходе ФИС при сканировании энергетического спектра пространствен-ной структуры ЛЗ узкой щелевой диафрагмой. Из (5.28) видно, что форма выходного сигнала ФИС повторяет форму спектра с точностью до коэфи-циента пропорциональности, зависящего от размеров полевой диафрагмы ФИС и коэфициента ![]() - масштаба КОС. Поэтому, измеряя амплитудно-временные параметры выходного электрического сигнала ФИС соответст-вующей аппаратурой, можно реализовать амплитудный метод контроля величины среднего квадратического отклонения ширины щелей в прост-ранственной структурк ЛЗ.
- масштаба КОС. Поэтому, измеряя амплитудно-временные параметры выходного электрического сигнала ФИС соответст-вующей аппаратурой, можно реализовать амплитудный метод контроля величины среднего квадратического отклонения ширины щелей в прост-ранственной структурк ЛЗ.
При амплитудном методе контроля с помощью КОС величины среднего квадратического отклонения ![]() ширины щелей в пространственной струк-туре ЛЗ необходимо на выходе ФИС измерять величину амплитуд отдельных максимумов ее энергетического спектра на частотых
ширины щелей в пространственной струк-туре ЛЗ необходимо на выходе ФИС измерять величину амплитуд отдельных максимумов ее энергетического спектра на частотых ![]() . Тогда, подставив
. Тогда, подставив ![]() в (5.28) с учетом, что
в (5.28) с учетом, что ![]() и выполнив ряд алгеб-раических преобразований можно показать, что амплитула
и выполнив ряд алгеб-раических преобразований можно показать, что амплитула ![]() -го максимума спектра, измеряемого на выходе ФИС, будет равна
-го максимума спектра, измеряемого на выходе ФИС, будет равна
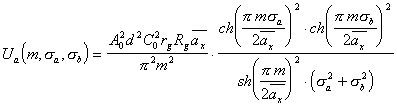 (5.29), а использовав тож-дество (653.4) из [20], амплитуду
(5.29), а использовав тож-дество (653.4) из [20], амплитуду ![]() -го максимума спектра представим в виде
-го максимума спектра представим в виде
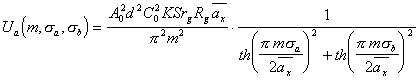 (5.30).
(5.30).
Из формулы (5.30) видно, что действительно с увеличением порядкового номера ![]() максимумов, амплитуда
максимумов, амплитуда ![]() их резко убывает.
их резко убывает.
Кроме того, с увеличением параметров ![]() либо
либо ![]() , амплитуда макси-мумов спектра убывает по обратнопропорциональной гиперболической
, амплитуда макси-мумов спектра убывает по обратнопропорциональной гиперболической
тангенциальной зависимости. Поскольку в результате статистических исследований было установлено, что ![]() является практически величиной постоянной [1] по сравнению с диапазоном измерений
является практически величиной постоянной [1] по сравнению с диапазоном измерений ![]() , то целесообраз-но рассматривать функциональную зависимость амплитуд максимумов спектра от параметра
, то целесообраз-но рассматривать функциональную зависимость амплитуд максимумов спектра от параметра ![]() , приняв
, приняв ![]() постоянным и равным 8 мкм.
постоянным и равным 8 мкм.
Однако линейная зависимость амплитуд ![]() максимумов спектра от освещенности
максимумов спектра от освещенности ![]() пространственной квазипериодической структуры ЛЗ приведет к значительным погрешностям амплитудного метода контроля лишь абсолютных значений амплитуд
пространственной квазипериодической структуры ЛЗ приведет к значительным погрешностям амплитудного метода контроля лишь абсолютных значений амплитуд ![]() максимумов спектра. Эти погреш-ности возникают из-за нестабильности выходной мощности излучения лазе-ра при температурных дрейфах его резонатора, которая достигает 20-30% от
максимумов спектра. Эти погреш-ности возникают из-за нестабильности выходной мощности излучения лазе-ра при температурных дрейфах его резонатора, которая достигает 20-30% от ![]() [19]. Поэтому, используя относительные измерения путем опреде-ления величины отношения
[19]. Поэтому, используя относительные измерения путем опреде-ления величины отношения  амплитуд
амплитуд ![]() -го и
-го и ![]() -го максимумов спектра
-го максимумов спектра
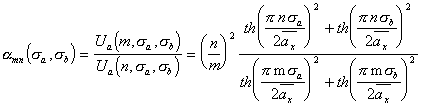 (5.31),
(5.31),
можно избавиться от влияния временных флуктуаций выходной мощности излучения лазера.
Полученное выражение (5.31) является уравнением амплитудного мето-да контроля величины СКО ![]() ширины щелей в пространственной структуре ЛЗ. В работе [1] показано, что для
ширины щелей в пространственной структуре ЛЗ. В работе [1] показано, что для ![]() и
и ![]() функция
функция  являет-ся монотонно убывающей по мере увеличения
являет-ся монотонно убывающей по мере увеличения ![]() . Однако крутизна измене-ния функции, характеризующая чувствительность метода, функционально зависит от соотношения номеров
. Однако крутизна измене-ния функции, характеризующая чувствительность метода, функционально зависит от соотношения номеров ![]() и
и ![]() , используемых для измерения максимумов. Поэтому для повышения чувствительности амплитудного мето-да контроля по алгоритму, описанному уравнением (5.31), необходима его оптимизация, т.е. выбор таких номеров
, используемых для измерения максимумов. Поэтому для повышения чувствительности амплитудного мето-да контроля по алгоритму, описанному уравнением (5.31), необходима его оптимизация, т.е. выбор таких номеров ![]() и
и ![]() максимумов, при которых достигается максимальная чувствительность функции
максимумов, при которых достигается максимальная чувствительность функции ![]() к изменению параметра
к изменению параметра ![]() . Согласно теории чувствительности [21, 22] - чувствитель-ность
. Согласно теории чувствительности [21, 22] - чувствитель-ность ![]() функции
функции ![]() к изменению СКО
к изменению СКО ![]() выражается ее первой частной производной по параметру
выражается ее первой частной производной по параметру ![]() , т.е.
, т.е.
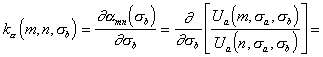
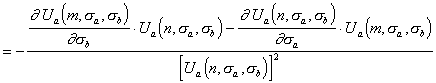 (5.32), а определив производные (5.30), которые равны
(5.32), а определив производные (5.30), которые равны
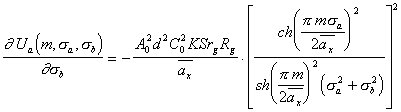 (5.33),
(5.33),
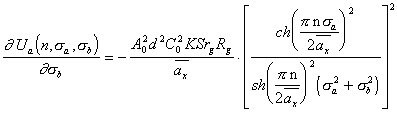 (5.34), и подставив (5.25), (5.33) и (5.34) в (5.32), а также выполнив ряд алгебраических преобразований, получим:
(5.34), и подставив (5.25), (5.33) и (5.34) в (5.32), а также выполнив ряд алгебраических преобразований, получим:
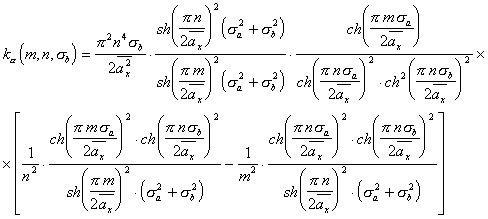 (5.35).
(5.35).
Анализ этого выражения выполнен в работе [1]. Получены следующие результаты:
чувствительность ![]() амплитудного метода контроля величины СКО
амплитудного метода контроля величины СКО ![]() при
при  повышается при выборе
повышается при выборе ![]() -го максимума спект-ра как можно высшего порядка;
-го максимума спект-ра как можно высшего порядка;
с увеличением порядкового номера ![]() , а также параметра
, а также параметра ![]() амплитуды максимумов резко уменшаются.
амплитуды максимумов резко уменшаются.
Это может привести к значительным техническим сложностям измере-ний на фоне шумов, а также к снижению чувствительности измерительной системы.
Поскольку шумы на выходе ФИС и статические характеристики квазипе-риодической структуры ЛЗ являются взаимонезависимыми величинами, то выходной сигнал ФИС представляет собой аддитивную смесь шумов с полезным сигналом. Поэтому минимальное значение амплитуды ![]() -го макси-
-го макси-
мума энергетического спектра, которое может быть аппаратурно зарегист-рировано по выходному сигналу ФИС, достигается при ![]() и должно быть в
и должно быть в ![]() раз больше величины среднего квадратического напряжения
раз больше величины среднего квадратического напряжения ![]() шумов ее приемника, т.е.
шумов ее приемника, т.е.
![]() (5.36), где
(5.36), где ![]() - требуемый коэфициент отношения сигнал/шум выходного сигнала фотоприемника ФИС. Тогда подставив (5.36) в уравнение (5.30) аиплитуд получим:
- требуемый коэфициент отношения сигнал/шум выходного сигнала фотоприемника ФИС. Тогда подставив (5.36) в уравнение (5.30) аиплитуд получим:
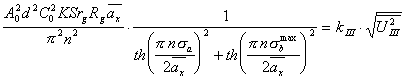 или
или
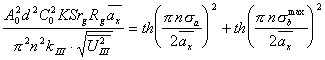 (5.37), откуда имеем
(5.37), откуда имеем
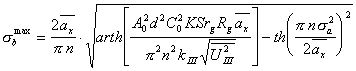 (5.38).
(5.38).
Полученное выражение (5.38) позволяет определить максимально допустимую величину СКО ![]() , доступную для контроля амплитудным ме-тодом, в зависимости от номеров используемых максимумов спектра и шу-мов ФИС. Из выражения (5.38) следует, что увеличить допустимое значение
, доступную для контроля амплитудным ме-тодом, в зависимости от номеров используемых максимумов спектра и шу-мов ФИС. Из выражения (5.38) следует, что увеличить допустимое значение ![]() можно путем уменшения шумов
можно путем уменшения шумов ![]() ФИС, либо увеличения освещен-ности
ФИС, либо увеличения освещен-ности ![]() квазипериодической структуры ЛЗ. Увеличение
квазипериодической структуры ЛЗ. Увеличение ![]() за счет по-вышения
за счет по-вышения ![]() достигается благодаря работе ФИС по пороговому сигналу лишь от одного, т.е.
достигается благодаря работе ФИС по пороговому сигналу лишь от одного, т.е. ![]() -го максимума. При этом амплитуда другого, т.е.
-го максимума. При этом амплитуда другого, т.е. ![]() -го максимума, не является пороговой для ФИС, поскольку в (5.31) она всегда больше амплитуды
-го максимума, не является пороговой для ФИС, поскольку в (5.31) она всегда больше амплитуды ![]() -го максимума.
-го максимума.
Похожие работы
... мере, синергетическим стилем мышления может быть некой платформой для открытого творческого диалога между учеными, мыслителями, деятелями искусства, имеющими различные творческие установки и взгляды на мир. 2. Некоторые парадоксальные следствия синергетики Множество новых парадоксальных идей, образов и представлений возникает в синергетике. Кроме того, с точки зрения синергетики может быть ...
0 комментариев