Студента I –го курса гр. 107
Шлыковича Сергея
Минск 2001
Вначале рассмотрим затухающие колебания.
Во всякой реальной колебательной системе всегда имеется сила трения (для механической системы), или электрическое сопротивление (для колебательного контура), действие которых приводит к уменьшению энергии системы. Если убыль этой энергии не восполняется, то колебания будут затухать.
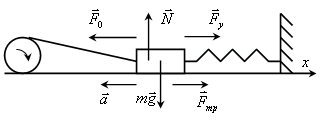
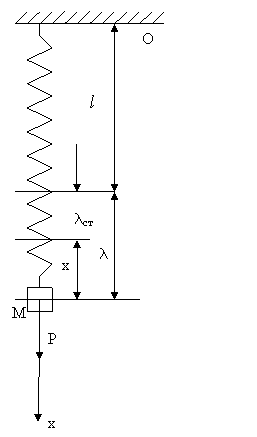
Рассмотрим механические колебания. В большинстве случаев сила трения пропорциональна скорости.
. (1.1)
Где r — постоянная, которая называется коэффициентом трения. Знак минус обусловлен тем, что сила F и скорость v направлены в противоположные стороны.
Уравнение второго закона Ньютона при наличии силы трения имеет вид
. (1.2)
Применим следующие обозначения
, 
(1.3)
Тогда
(1.4)
Где щ0 — собственная частота колебательной системы.
Будем искать решение уравнения в виде
(1.5)
Найдём первую и вторую производные
Подставим выражения 
в уравнение (1.5)
Сократим на 
(1.6)
Решение уравнения (1.6) зависит от знака коэффициента, стоящего при и. Рассмотрим случай, когда этот коэффициент положителен (т. е. b<щ0 — трение мало). Введя обозначение , придем к уравнению
Решением этого уравнения будет функция 
Подставляя это выражение в уравнение (1.5), имеем
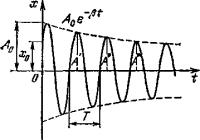
(1.7)
Здесь A0 и б — постоянные, значения которых зависят от начальных условий, щ — величина, определяемая формулой
.
Скорость затухания колебаний определяется величиной , которую называют коэффициентом затухания.
Для характеристики колебательной системы употребляется также величина
называемая добротностью колебательной системы. Она пропорциональна числу колебаний Ne , совершаемых системой за то время t, за которое амплитуда колебаний уменьшается в e раз.
Вынужденные колебания.
Допустим, что механическая колебательная система подвергается действию внешней силы, изменяющейся со временем по гармоническому закону:
(2.1)
В этом случае уравнение второго закона Ньютона имеет вид
Введя обозначения (1.3), преобразуем уравнение приобретёт вид:
(2.2)
Здесь b — коэффициент затухания, щ0 — собственная частота колебательной системы, щ — частота вынуждающей силы.
Дифференциальное уравнение (2.2) описывает вынужденные колебания. Решение этого уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения. Общее решение однородного уравнения уже найдено (1.7), оно имеет вид
(2.3)
Где 
.
Попробуем найти частное решение (2.2) в виде 
(2.4)
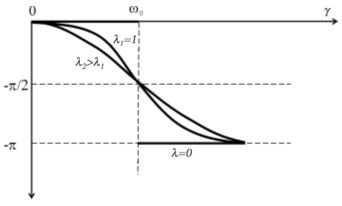
где 
— неизвестный пока сдвиг фаз между силой и вызываемыми ею колебаниями.
(2.5)
(2.6)
Развернем 
и по формулам для синуса и косинуса разности и подставим в формулу (2.2) 
:
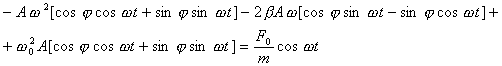
Сгруппируем члены уравнения:
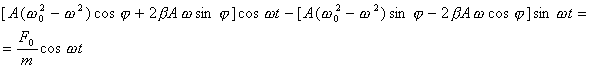
(2.7)
Уравнение (2.7) будет тождественно при любых значениях t тогда, когда коэффициенты при cosщt и sinщt в обеих частях уравнения будут одинаковыми.
(2.8)
(2.9)
Найдём значения A и 
при которых функция (2.4) удовлетворяет уравнению (2.2). Для этого возведём равенства (2.8) и (2.9) в квадрат и сложим их друг с другом
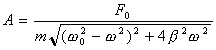(2.10)
Из (2.9) следует, что
(2.11)
Подставим значения A и 
в (2.4) и получим частное решение неоднородного уравнения (2.2):
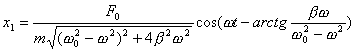(2.12)
Общее решение имеет вид
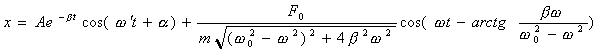
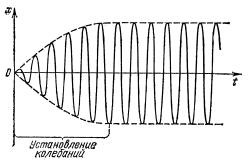
Первое слагаемое играет заметную роль только в начальной стадии процесса, при установлении колебаний. С течением времени из-за экспоненциального множителя роль слагаемого уменьшается, и по прошествии достаточного времени им можно пренебречь, сохранив в решении только второе.
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы (2.10) приводит к тому, что при некоторой частоте амплитуда достигает максимального значения. Колебательная система оказывается особенно отзывчивой на действие вынуждающей силы при данной частоте. Это явление называется резонансом, а соответствующая частота — резонансной частотой.
Для того чтобы определить резонансную частоту щрез, нужно найти максимум функции (2.10), т.е. продифференцировать это выражение по щ и приравняв производную нулю:
Решения этого уравнения щ=0 и 
, но два из них исключаются, т.к. решение, равное нулю, соответствует максимуму знаменателя, а 
не имеет физического смысла (частота не может быть отрицательной).
(2.13). Следовательно (2.14)
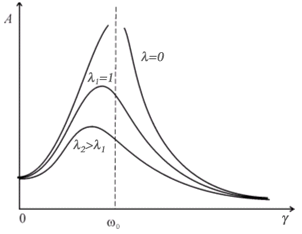
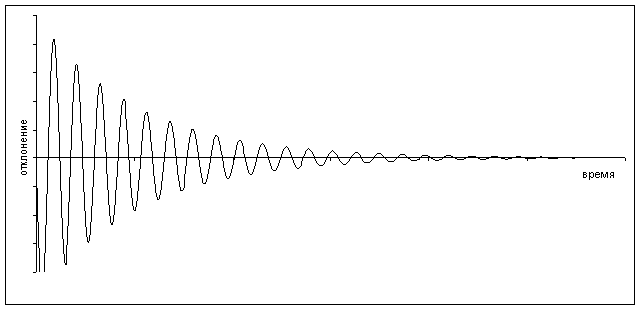
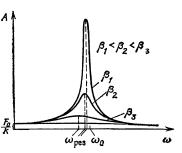Зависимость амплитуды вынужденных колебаний от частоты колебаний показана графически на рисунке слева. Кривые на графике соответствуют различным значениям параметра b. Чем меньше b, тем выше и правее лежит максимум резонансной кривой. При очень большом затухании (таком, что b2 > щ0) выражение для резонансной частоты становится мнимым. Это означает, что резонанс в этом случае не наблюдается — с увеличением частоты амплитуда монотонно убывает.
Изображенная на рисунке совокупность графиков функции (2.10) называется резонансными кривыми.
Согласно формуле (2.14) при малом затухании (т. е. при b<<щ0) амплитуда при резонансе 
Если разделить это выражение на смещение x0 из положения равновесия под действием постоянной силы F0, равное . В результате получим, что
где 
- логарифмический декремент затухания.
Следовательно, добротность Q показывает, во сколько раз амплитуда при резонансе превышает смещение системы из положения равновесия под действием постоянной силы, модуль которой равен амплитуде вынуждающей силы (это справедливо лишь при небольшом затухании).
Литература:
И. В Савельев “Курс общей физики”.
P.S.
Данная лит-ра использовалась также при написании реферата на тему «Сложение колебаний».
Похожие работы
... частоты вынуждающей силы) характеристики. Графически эти зависимости при различных значениях приведены на рисунках 5 и 6: Рис.5 Амплитудно-частотные характеристики Рис.6 Фазово-частотные характеристики Отметим здесь, что в отсутствие трения изменение фазы вынужденных колебаний на величину происходит скачком при . Учет трения размазывает этот скачок. При установившемся ...
... уравнение в виде: или, обозначив с/m через k2, (1) Полученное уравнение определяет так называемые свободные колебания груза. Оно называется уравнением гармонического осциллятора. Это линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его характеристическое уравнение: имеет мнимые корни , соответственно этому общее решение Для выяснения ...
... потенциальной энергии появляется член — xF(t), так что функция Лагранжа системы будет: (2,1) Соответствующее уравнение движения есть или (2,2) где мы снова ввели частоту со свободных колебаний. Как известно, общее решение неоднородного линейного дифференциального уравнения с постоянными коэффициентами получается в виде суммы двух выражений: х = х0 + ...
... интенсивностью волны. Таким образом, интенсивность сферической волны убывает обратно пропорционально квадрату расстояния от источника. 1 4 1 2 Применение.Областью применения колебаний и волн служат многие изобретения человека: от музыкальных инструментов и акустических динамиков до эхолотов и ультразвуковых диагностических аппаратов . С тремя последними мы и ...
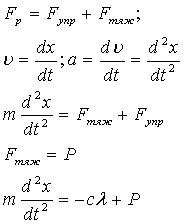
0 комментариев