X [100]

 7 X [100]  

5 6 [111]

Y a) b)  c)

Каждой кристаллографической плоскости соответствует различная плотность _________ атомов, поэтому и различие в свойствах.

1,4 2,3 4 3 2 4 1,3 2

1,8

5,6 7,8 5 7 5 6,8 7

 6

 

а) b) c)

НОСИТЕЛИ ЗАРЯДА В ПП.

Электропроводность вещества объясняется наличием свободных носителей заряда, которые могут перемещаться в объёме вещества, либо под воздействием поля, либо при наличии градиента их концентрации в веществе (стремление к выравниванию концентрации).

Как же образуются свободные носители заряда в ПП?

Идеальный ПП при Т = абсолютному нулю (ПП не имеет дефектов кристалла, поэтому валентные е всех атомов участвуют в ковалентных связях, т.е. они не свободные) является идеальным диэлектриком. При повышении Т°(*) электроны приобретают дополнительную энергию и в конечном итоге некоторые ковалентные связи разрываются, образуя свободные е и незаполненную связь – «дырку» вблизи атома с недостающим е (образуется электронная дырочная пара). Такой процесс называется термогенерацией. Отсутствие е недолговечно (время жизни), на его место приходит е из соседних атомов (рекомбинация), т.е. «дырка» дрейфует. Такая проводимость ПП называется собственной проводимостью, а ПП – собственным ПП (особенность – количество е всегда равно количеству «дыр»).

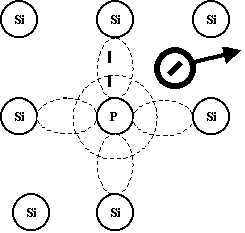
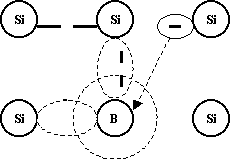
Интересные явления наблюдаются при замещении некоторых атомов Si так называемыми примесными (примесь замещения, есть ещё и примесь внедрения) атомами другой валентности (3 и 5) (копр. 5 вал. Р или 3 вал. бор, Аl).

a) b)

В первом случае 9 е атома фосфора легко «отрывается» от него образуя ион +, а е добавляется к собственным свободным е и равновесие – «дырка» нарушается. Проводимость становится преимущественно е – нной (n – проводимость).

Во втором случае все 3 е бора связаны с соседними атомами Si, образуя «дырку», а атом примеси превращается в неподвижный ион -. ПП приобретает дырочную (Р) проводимость. Такие проводимости называются примесными проводимостями. Носители, находящиеся в большинстве, называются основными, другого типа не основными.

ПАРАМЕТРЫ ПОЛУПРОВОДНИКОВ

е отдельно взятого атома зависит от того, на какой оболочке он находятся, имеют строго одиночное значение энергии. Под влиянием межатомных сил в кристалле эти энергетические уровни расширяются и превращаются в энергетическую зону (Эффект Штарка). Нас будет интересовать энергетическая зона внешней оболочки (т.н. валентная зона). Для того, чтобы е покинул валентную зону и стал свободным, обеспечивающим проводимость, ему необходимо сообщить определённую дополнительную энергию, после чего он попадает в так называемую зону проводимости.

Величина дополнительного энергетического импульса различна для различных полупроводников и определяет ширину так называемой запрещённой зоны. Собственно, ширина запрещённой зоны, а, следовательно, и вид зонной диаграммы, и отличает ПП от диэлектрика.

W(энергия)

j  Зона проводимости

 Зона проводимости

 донорная(n)

примесь Запрещённая зона

 Запрещённая зона {

акцент.(р)

Валентная зона примесь Валентная зона

 

 ПП Диэлектрик

Таким образом, ширина запрещённой зоны определяет энергию, необходимую для перехода е из валентной зоны в зону проводимости, и является важнейшим параметром ПП. Если е возвращается в валентную зону, то происходит рекомбинация е и дырки.

В электронике оценка энергии е производится величиной

W = gj, где

j - потенциалов, прошедших элементарным зарядом (иногда, энергетическим потенциалом).

В зависимости от количества атомов примеси и от энергии, получаемой е внешних оболочек (в частности от Т° ПП) количество е зоны проводимости будет различно. Но ведь количество носителей тока при наличии поля будет определять, в частности, величину тока в ПП. Поэтому количество таких е («дырок») является важным параметром. Однако, само количество е («дырок») ещё ни о чём не говорит. Важна их концентрация (т.е. количество на единицу объёма).

Концентрация носителей (обозначается n – для е и p – для «дырок») – очень важный параметр ПП. Концентрация сильно зависит от Т° (например, увеличение Т на 5% увеличивает концентрацию на ~ 3 раза) и от ширины запрещённой зоны (обратно пропорционально). В ПП концентрация носителей неравномерна ( т.е. существует градиент концентрации). Такое неравномерное распределение носителей называется Больумановским равновесием и объясняется возникновением внутреннего электрического поля в ПП, препятствующего выравниванию концентрации.

Движение носителей в электрическом поле напряжённостью Е называется дрейфом и величина дрейфового тока:

i = sE, где

s - удельная проводимость, важный параметр ПП (иногда используют удельное электросопротивление r = 1/s).

Т.к. в ПП есть 2 типа носителей, то

s = qnmn + qpmp,где

q – единичный заряд

n и p – концентрация

mn и mp – подвижность носителей, важный параметр ПП.

В вакууме носитель под воздействием поля Е будет двигаться равноускоренно. Другое дело – твёрдое тело. Ускоряясь, носители постоянно «сталкиваются» с атомами (испытывают рассеяние). На длине свободного пробега носители двигаются равноускоренно, затем, столкнувшись, теряют скорость и снова ускоряются. Поэтому средняя дрейфовая скорость _

J = mЕ, где

m - коэффициент пропорциональности, называемый подвижностью носителя, и зависящий от его эффективной массы (для Si me ~ 3mp).

Быстродействие полупроводниковых приборов прямо пропорционально подвижности носителей ПП, на основе которого выполнен прибор.

Подвижность – величина не постоянная и зависит от Т°, причём неоднозначно, например

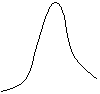
m Так, для Si m могут меняться в диапазоне рабочих температур

от -50°С до +125°С в 4-5 раз.

Т

ЭФФЕКТ ПОЛЯ

Эффект поля – это изменение концентрации носителей (а, следовательно, проводимости) в приповерхностном слое ПП под воздействием внешнего электрического поля.

Создадим конструкцию МДП:

+ d ++ +++

· · Т.к. есть диэлектрик, то ток не течёт. Из-за свойств

Me Eд диэл. -- U + проводника все свободные е сосредоточены на

поверхности проводника. На обкладке, представляющей

 собой ПП будет наведён такой же заряд, что и в провод

нике, однако, он будет распределён неравномерно в глубь

 кристалла.

Поле в диэлектрике, ввиду отсутствия объёмных

X зарядов, постоянно. В ПП р-типа, при подаче +U

на ПП, на границе ПП – диэлектрик концентрация

U изменений р – типа увеличивается, следовательно,  увеличивается и проводимость. Увеличение концентрации оситных носителей в слое называется обогащением (уменьшение – объединением при неизменной полярности U ). По мере уменьшения d эффект поля может исчезнуть за счёт пробоя диэлектрика. Даже если диэлектрик – вакуум, возможен туннельный эффект. Глубина проникновения поля в ПП (фактически, толщина обогащённого слоя) называется длиной Дебая (дебаевская длина). ЭЛЕКТРОННО-ДЫРОЧНЫЕ ПЕРЕХОДЫ

В подавляющем большинстве случаев в микроэлектронике находят применение так называемые p-n переходы, возникающие на границе металл – полупроводник и полупроводник – полупроводник. Комбинация двух ПП различной проводимости обладают вентильными свойствами, т.е. они лучше пропускают поток в одном (прямом) направлении. Практически все реальные p-n переходы - плавные, т.е. в районе металли

p-n переход ческой границы концентрация одних примесей

p n

постоянно растёт, а других – убывает. Сама металли

ческая граница характеризуется равенством p=n.

 Как правило, концентрация p и n вне границы

металлическая граница существенно различаются, и такие p-n переходы

называются асимметричными (несимметричными).

Т.к концентрация n > p, то число электронов, диффундирующих в область р больше, чем число диффундирующих «дырок» и в слое р вблизи границы оказываются избыточные е, ре-комбинирующие с «дырками» до тех пор, пока не будет равновесия. Следовательно, концентрация «дырок» уменьшится. Аналогично можно рассуждать и по отношению к «дыркам».

Например:

асимметрия

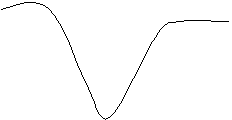
n n,p

p

идеальный

переход

Х

В идеале считают, что в p-n переходе Ширина перехода (d)

вообще отсутствуют носители и сам p-n переход является наиболее высокоомной частью структуры. Т.к. концентрация p и n различна, то между p и n областями, разделёнными высокоомным переходом, возникает потенциальный барьер. Если к переходу приложить напряжение + и к p-области (такая полярность называется прямой), то высота потенциального барьера уменьшится и

уменьшится его ширина. При обратной номерности - высота барьера и его

n p

ширина увеличатся. При прямых напряжениях в каждой из областей появляются избыточные носители и тогда говорят об инжекции носителей, если напряжение обратное, то количество носителей уменьшается, и говорят об

·- + ·

(+) (-)

экстракции носителей. Причём, если переход симметричный, то инжекция ( экстракция) е и «дырок» - одинаковая. Если переход асимметричный, то считают, что инжекция имеет односторонний характер и главную роль играют носители, инжектируемые из низкоомного (легированного) слоя в высокоомный. Низкоомный (более легированный) слой эмиттером, а высокоомный – базой. Таким образом, если к p-n переходу приложить прямое напряжение, то это приводит к изменению концентрации инжектированных носителей в области базы, а следовательно, изменяется и величина накопленного заряда, обусловленного этими зарядами. Процесс накопления избыточного заряда эквивалентен процессу заряда ёмкости. Поэтому говорят, что p-n переход обладает диффузионной ёмкостью.

Помимо диффузионной p-n переход обладает и барьерной (зарядной) ёмкостью (Сб) (если к p-n переходу приложить обратное напряжение, то на металлической границе носители отсутствуют и мы имеем ярко выраженную ёмкость). Сд и Сб – нелинейные ёмкости. Сд в основном проявляется при прямом включении диода, а Сб – при обратном. Первая зависит от тока Iпр, вторая – от Uобр. Строго говоря, такое разделение чисто условное, но оно удобно при анализе переходных процессов.

Сд и Сб существенно влияют на частотные свойства p-n перехода. Аналитически можно показать, что ВАХ такого p-n перехода описывается экспоненциальной зависимостью (Степаненко стр 82) вида: I/I0

I = I0(e(U/jт) – 1), где

jт – температурный потенциал ~ 25 милливольт

 I0 – тепловой ток, сильно зависящий от Т° p-n перехода. · ·

Можно доказать, что:  2 4 U/jт

I0(Т) = I0(Т0)2 DТ/Т*, где

Т0 – средняя температура некоторого температурного диапазона, например - комнатная

DТ – температура - градиент

Т* - так называемая температура удвоения.

В частности для кремния:

I0(Т) @ I0(20°С)2 (Т-20°С /10°С)

Т.е. считают, что I0 изменяется в 2 раза при изменении Т перехода на 10°С (по другим источникам Т* = 5°С).

Прямая ветвь ВАХ довольно крутая и можно считать, что падение U на таком переходе = const практически во всём диапазоне изменения рабочих токов, и при расчётах, обычно, полагают, что

Uдиода пр = 0,7В для нормального режима и

Uдиода пр @ 0,5В на микротоках

ПРОБОЙ P-N ПЕРЕХОДА

На приведённой выше ВАХ изображён только начальный участок обратной ветви. Как пойдёт обратная ветвь при дальнейшем увеличении Uобр?

Дальше – пробой p-n перехода.

Различают три вида (механизма) пробоя: лавинный, туннельный и тепловой.

А) Лавинный пробой происходит если Uобр  

ширина p-n перехода (d) больше длины

свободного пробега.

d ³ l

В этом случае, не основные носители, ускоряясь  Uпробоя в переходе, могут приобрести энергию, достаточную  

для ионизации атомов кристаллической решётки.

Выбитые е в свою очередь, ускоряясь, принимают  

участие в дальнейшей ионизации. Процесс 1 2 3 I обр носит лавинный характер (ветвь 1).

Скорость нарастания тока характеризуется коэффициентом ударной ионизации,  

который зависит в основном от распределения примесей (строго говоря – от

напряжённости электрического поля Е в данной точке). При таком пробое

rp-n = dU/dI

резко уменьшается. Однако, напряжение Up-n не может стать ниже Uпробоя т.к. Е станет < Е ионизации. Поэтому ветвь почти строго вертикальна.

Этот пробой используют для создания ПП приборов – стабилитронов (дать параметры и схему).

В) Туннельный пробой(ветвь 2).

Если d < l, то лавинный пробой невозможен, т.к. носители практически не сталкиваются с атомами решётки. Но возможно туннелирование носителей (см. туннельный эффект). Для уменьшения вероятности такого пробоя, базу изготавливают низколегированной (с высоким сопротивлением), а также увеличивают d (тогда U пробоя увеличивается).

С) Тепловой пробой.

Обратный ток p-n перехода повышает температуру перехода, что, в свою очередь, приводит к увеличению обратного тока и т.д. Если не принимать мер по отводу тепла, то саморазогрев перехода может привести к тепловому пробою (кривая 3).

Отличительная особенность – участок с отрицательным дифференциальным сопротивлением. Iобр зависит от ширины запрещённой зоны, поэтому тепловой пробой при прочих равных условиях чаще будет наблюдаться в Ge, чем в Si. Обычно I обр малы и тепловой пробой сам по себе редко наступает, но может возникнуть, как сопутствующий лавинному или туннельному пробоям. Если в схеме нет строго ограничивающих компонентов, то тепловой пробой приводит к невозвратимому разрушению прибора.

КРАТКАЯ ХАРАКТЕРИСТИКА РАЗЛИЧНЫХ ТИПОВ ПП ДИОДОВ

1) Стабилитроны – имеют оригинальную обратную ветвь ВАХ(лавинный пробой)

2) Туннельные диоды (ТД) – Основаны на туннельном эффекте. Прямая ветвь ВАХ такого диода имеет участок с отрицательным дифференциальным

Сопротивлением, что позволяет создавать генераторы, смесители, I

Переключатели на основе таких p-n переходов. ТД работают

только на основных носителях, следовательно, Сдифф = 0,

поэтому частотные свойства высокие. Изготавливаются ТД

из сильнолегированных ПП. U

3) Импульсные, высокочастотные и СВЧ диоды. Т.к. обычный p-n переход обладает Сд и Сб, и является инерционным прибором, то на время накопления и рассасывания заряда а базе p-n переход теряет выпрямительные свойства. Для характеристики этих свойств p-n перехода принято 2 параметра:

а) время установления rпрямое

в) время восстановления rобратное

Чем меньше эти времена, тем выше частотные свойства

Импульсные fпереключателя > 1мГц

Вч fпереключателя > 150мГц

ВЧ fпереключателя > 1ГГц

4) Диоды Шоттки образуются на границе металл – полупроводник. Работает только на основных носителях (Сд = 0). Уменьшая площадь перехода, уменьшают Сб. Поэтому fпереключателя = 3 – 15 ГГц.

Применяется очень широко.

5) Фотодиоды – основаны на изменениях проводимости в зависимости от освещённости.

6) Светодиоды – используется явление изменения света в некоторых широкозонных ПП (фосфид галия, карбид кремния и т. д.) при рекомбинации е и «дырок».

Гетеропереходы, диоды с накоплением заряда, варикапы, параметрические диоды,

инжекупонные фотодиоды, фотоэлементы координатно-чувствительные фотоприёмники, лазер на основе p-n перехода, инжекупонный гетеролазер, варисторы – особенности этих специфических p-n переходов

см. [6] Вакулин, Стафеев «Физика ПП приборов».

Ранее были гомопереходы.

Гетеропереход – переход между ПП различной физико – химической природы (например Si – Ge, Si – GaAs, GaAs – GaP(фосфид галия)), причём это не обязательно p-n переходы, могут быть и n-n, p-p (различная ширина запрещённой зоны в полупроводниках)

Диоды с накоплением заряда – для формирования фронтовых сигналов.

Вариканы – ёмкость(барьерная), управляемая U

Варисторы – нелинейное полупроводниковое сопротивление

БИПОЛЯРНЫЕ ТРАНЗИСТОРЫ(Т)

Транзистором называют ПП прибор, обладающий усилительными свойствами по мощности. Именно усиление мощности характеризует транзистор, как усилительный прибор. Нельзя говорить о транзисторе, как об усилителе тока. Тогда трансформатор тока является усилителем, хотя известно, что он усиливает ток , но «гасит» напряжение. Аналогично и транзистор напряжения – увеличивает напряжение за счёт тока.

По принципу действия различают:

- биполярные Т

- униполярные Т

Название Т определяется типом носителя в транзисторе:

основные

биполярные униполярные один тип - основной

неосновные

Биполярный транзистор представляет собой совокупность взаимодействующих встречно – включённых p-n переходов, имеющих общую область – базу.

 р

Э Б К

n+ n

n1 ^ ^ ^ W

Э   К

n2

Б

p a) б)

Рабочей зоной является донная зона эмиттера. Тогда Т можно изобразить . Обычно, концентрация n1 >> n2, на б) это отражается значком n+. Сильно легированный электрод с меньшей площадью называется эмиттером, менее легированный с большей площадью – коллектором (собирающий). Процессы в переходах n1 – p и n2 – p взаимно влияют друг на друга, т.к. толщина базы W<1мк и существенное влияние на работу Т оказывает база (Б).

Концентрация носителей в Б может быть равномерной (однородная база), поле в Б отсутствует и движение носителей – диффузия. Такие Т называются диффузионными или бездрейфовыми.

Если примеси распределены неравномерно (см. Больюмановское равновесие в «Параметры ПП»), то в такой Б будет присутствовать внутреннее поле и движение носителей определяется не только диффузией, но и дрейфом. Такие ПП называются дрейфовыми (практически все ИМС)

На рис.б) изображён n – p – n транзистор. Может быть и p – n – p. Разница в полярности напряжений.

РЕЖИМИ РАБОТЫ ТРАНЗИСТОРА

OO

h + P - n

Э - O O +К IЭ IК

O _

O Iб

IЭ IК

 

+ Б -

Iб (ток, обусловленный рекомбинацией)

При нормальном включении переход ЭБ смещают в прямом направлении, а БК – в обратном. При этом эмиттер инжектирует в Б е, которые, ввиду узости Б, очень незначительно рекомбинируют с «дырками», образуя Iб, а большая часть «пролетает» Б и собирается коллектором. При таком включении напряжений коллектор способен собирать только е, поэтому Э должен в основном содержать электролизные составляющие. Для этого область Э выполняют сильно легированной (n+).

В таком режиме токи IК и IЭ почти одинаковы:

IЭ = IК + Iб

Iб очень малый и обусловлен рекомбинацией основных носителей в области базы, а также инжекцией «дырок» из базы в эмиттер.

Обратно смещённый коллекторный переход имеет большое сопротивление (сотни кОм – единицы мОм) поэтому включение в цепь коллектора достаточно больших сопротивлений нагрузки практически не повлияет на величину IК, а на Rн будет выделяться большая мощность.

Сопротивление БЭ – мало (20 ¸ 30 Ом), а через него протекает практически такой же ток, как и IК. Однако, мощность, выделяемая в цепи эмиттера, намного меньше, чем мощность Rн. Это свидетельствует о том, что транзистор является усилителем мощности. Фактически, усиление в Т получается за счёт модуляции сопротивления коллекторного p-n перехода.

Т в цифровых схемах часто работает не в вышеуказанном режиме, а в режиме насыщения (более правильным будет название – режима двойной инжекции – как со стороны эмиттера, так и со стороны коллектора). Такой режим возможен, если оба перехода – ЭБ и КБ будут смещены в прямом направлении. Тогда К, (также как и Э) инжектирует е в базу, а собирает их эмиттер. Электроны, инжектируемые Э – собирает К. Из положения транзистора видно, что он является симметричным прибором, т.е. коллектор и эмиттер в принципе можно менять местами.

Такое включение Т называется инверсным включением. Однако на практике оно использу ется редко, т.к. параметры такой схемы хуже, чем ранее рассмотренной (концентрация n2<<n1, а следовательно е составляющего тока < , площадь К < площади Э).

Если оба перехода смещены в обратном ( непроводящем) направлении, то инжекция носителей в Б отсутствует, через переходы протекают обратные токи.

Такой режим называют режимом отсечки.

СИСТЕМЫ ПАРАМЕТРОВ ТРАНЗИСТОРОВ

При расчёте схем удобно представлять Т в виде «чёрного ящика» - четырёхполюсника.

I1 I2

· ·

U1 · · U2

Все величины взаимосвязаны и эта связь определяется статистическими параметрами четырёхполюсника (транзистора). Если известны 2 величины, то недостающие 2 можно определить по статическим характеристикам. Всего можно написать 6 зависимостей между входными и выходными величинами, но на практике находят применение 3 из них

n1 = ¦1(I1,I2) n2 = ¦2(I1,I2)

I1 = j1(U1U2) I2 = j2(U1U2)

U1 = y1(I1n2) I2 = y2(I1U2)

Рассматривая зависимости в области малых сигналов (приращений), и раскладывая их в ряд Тейлора, можно получить 3 системы параметров: Z – параметры, Y – параметры и h – параметры. Имея одну систему параметров аналитическим путём несложно получить другие.

На практике Z – параметры (такая система называется системой полных сопротивлений) и Y – параметры (система полных проводимостей), ввиду трудности их экспериментального определения, используются редко. Чаще используются гибридные h – параметры. В этом случае четырёхполюсник описывается системой уравнений:

J1 = h11i1 + h12J2

i2 = h21i1 + h22J2, где

J1,J2, i1, i2 – малые изменения (приращения) входных и выходных величин 4-х полюсника.

h11 = J1/ i1|J2 = 0 – входное сопротивление транзистора при короткозамыкающем  

выходе

h12 J1/J2| i1 = 0 – коэффициент обратной связи по напряжению при холостом входе

во входной детектор

h21 i2/i1|J2 = 0 – коэффициент передачи тока при КБ выходе

h22 i2/J2| i1 = 0 – выходная проводимость при входе во входную цепь

СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТРАНЗИСТОРА

СХЕМА ЗАМЕЩЕНИЯ

h, Y и Z параметры используются при расчётах электронных схем, однако, они плохо поясняют физические процессы, протекающие в транзисторе. Для этого используются физические модели или по-другому эквивалентные схемы (схемы замещения). Таких моделей м.б. несколько. На практике широкое применение получила модель Эберса – Молла (Молла – Эберса).

· К

Iк

rk

Uбк 1

I2 h21БI1

rб

Б

Iб I1

h21БiI2

2

Uбэ Iэ

rэ

I1 = ¦(Uбэ)

 I2 = ¦(Uбк)

Э

В некоторых не учитываются резисторы rэ, rk, rб, отражающие наличие пассивных областей транзистора. Рисунок отражает полную эквивалентную схему транзистора в режиме двойной инжекции. Ток, инжектируемый из Э в Б, обозначен I1, ток, инжектируемый из К в Б, обозначен I2. Инжектируемый эмиттером ток I1 собирается коллектором. Он представлен на схеме генератором тока h21БI1, где h21Б – коеффициент передачи тока I1 в область коллектора (всегда >1, т.к. носители частично рекомбинируются в области базы). [Источник тока имеет rвн ®¥ и генерирует фиксированное (стабильное) значение тока в нагрузку, независимо от величины Rн].

Инжектируемые коллектором ток I2 собирается эмиттером (на схеме – источник тока h21БiI2), где h21Бi – коэффициент передачи I2 в область эмиттера. h21Бi < h21Б.

Эквивалентные схемы, отображающие работу транзистора в других режимах, будут отличаться от приведённой. Например, если отсутствует режим насыщения, то в эмиттерной области будет отсутствовать источник h21БiI2.

Согласно 1-му закону Кирхгофа можно записать:

Iэ = I1 - h21БiI2 (1)

Iк = h21БI1 - I2

Известно, что ВАХ p-n перехода описывается экспоненциальной зависимостью (см. электронно – дырочный переход). Тогда:

I1 = I`эо(e (Uбэ/jт) - 1)  (2)

I2 = I`ко(e (Uбк/jт) - 1)

Подставляя (2) в (1), получаем аналитическое описание ВАХ транзистора:

Iэ = I`эо(e (Uбэ/jт) - 1) - h21БiI`ко(e (Uбк/jт) - 1) (3)

Iк = h21б I`эо(e (Uбэ/jт) - 1) - I`ко(e (Uбк/jт) - 1)

Из схемы можно записать значение Iб:

Iб = Iэ – Iк (4)

Подставив (3) в (4) получим:

Iб = (1- h21б) I`эо(e (Uбэ/jт) - 1) + (1- h21бi) I`ко(e (Uбк/jт) - 1) (5)

Уравнения 3,4,5 называются уравнениями Эберса – Молла. В зависимостях I`эо и I`ко – тепловые, а не обратные токи переходов.

I`ко = Iко/(1 - h21бh21бi); I`эо = Iэо/(1 - h21бh21бi)

В приведённых зависимостях все напряжения мы задавали относительно базы. Такая схема включения Т называется схемой с ОБ (схема а)). Такое включение в схемотехнике используется только для реализации источников тока и встречается редко. (малое Rbx, Ki<1). Наиболее широкое распространение получила схема с ОЭ (схема b)).

Iк

+

Iэ Iк Iб

Uкэ

- + +

+ Uбэ Uбк - Uбэ

Iб - Iэ -

a) b)

Иногда используется и схема с ОК (схема с)).

Т.к. прямая ветвь ВАХ p-n перехода довольно крутая, то задавать прямое напряжение на

p-n переходе при анализе схем включения Т практически нереально. Поэтому задаётся,

Iб u  как правило, прямой ток. Рассмотрим соотно

шение между токами транзистора.

+ p Uкэ Известно, что ток Iэ ¹ Iк (Iэ > Iк), т.к. суще

ствует рекомбинация носителей в области

Uбк n базы. Между Iэ и Iк существует соотноше

+ ние:

Iк = h21б Iэ, где (6)

h21б – коэффициент передачи тока эмиттера в область коллектора. h21б<1, но довольно близок к 1 (h21б = 0,99 ¸ 0,9) (h21б иногда a).

Можно доказать, что 2

h21б » 1 – 0,5(W/L) , где

W – ширина базы

L – длина свободного пробега носителя

Отсюда видно, что для получения большего значения h21б следует уменьшить толщину базы. Известно, что Iэ = Iк + Iб, т.к. Iк = h21б Iэ, то

Iк/ h21б = Iк + Iб; откуда Iк = h21б/(1 - h21б )Iб

Величина h21б/(1 - h21б ) = h21э – коэффициент потока Iб в коллекторную цепь для схемы с ОЭ (иногда b).

Тогда Iэ = Iк + Iб = (h21э + 1)Iб.

Рассмотренные выше соотношения получены для схемы с ОБ. Особенностью этой схемы является то, что входной величиной является ток эмиттера. Т.к. база общая с К, потенциал Б – фиксирован. Т.к. переход база – эмиттер смещён в прямом направлении, то малое изменение Uбэ приводит к существенному изменению Iэ, что свидетельствует о малой величине Rвx схемы с ОБ. Rвx » rб + (rэ/ (h21э + 1))

Т.к. через rэ протекает ток Iэ » Iб h21э, то считают, что rэ трансформируется во входную цепь с коллектором.

Что касается коэффициента усиления по току схемы с ОБ, то

К +/- = Iвых/Iвх = Iк/ Iэ » h21б < 1

Выходное сопротивление схемы ОБ:

Rвыx = DUвых /DIвых = DIк(Rк||rкб)/DIк » Rк||rкб

En rn = 0 В зависимости Rк||rкб, т.к. со стороны выхода

Rк Rк (нагрузка) и rкб (сопротивление обратно -

смещённого перехода БК) включены парал-

Вых лельно. Сопротивление пассивной области К

rк << rкб или им можно пренебречь.

На практике наиболее широкое применение

rкб находит схема с ОЭ.

Т.к. приращение DUвх вызывает приращение

DIвх = DIб в h21э раз меньшее, чем входной

Б ток схемы с ОБ (там DIвх = DIэ), то

rб Rвxоэ = DUвх /DIвх » RвxОБ h21э

и составляет величину порядка сотен ОМ – несколько кОМ.

Коэффициент усиления по току:

Кi = DIвых/DIвх = DIк/DIб = h21э

Можно показать, что схема обладает достаточно большим

Кu » h21эRк/( rб + rэ/ h21э)

Т.к. нагрузка включена в коллекторную цепь (также как и в схеме ОБ), то входное сопротивление примерно равно RвыxОБ, т.е.

Rвыxоэ » RвыxОБ » Rк||rбк

или, учитывая Rк << rкб Rвыxоэ » Rк

и составляет величину порядка единиц кОМ.

Схема с ОК используется в схемотехнике ЦВМ сравнительно редко (например ЭСЛ) и её можно характеризовать следующими параметрами:

Кi » h21э + 1 (большой)

Кu » h21э < 1

Rвx » Rэ(h21э + 1) – достаточно большое (десятки кОМ)

Rвыx » Rэ/(h21э + 1) – достаточно малое (единицы ОМ)

Для определения параметров транзистора и режимов работы в схеме используются статические характеристики Т. Различают входные и выходные характеристики. (Передаточные характеристики используются редко).

Входной статической (далее термин «статический» будем опускать) характеристикой Т называется зависимость тока его входного электрода от напряжения на нём при определённых включениях тока или напряжения на входных электродах. Например, для схемы с ОЭ это

Iб = ¦(Uбэ) при Uкэ = const.

Выходная характеристика – зависимость его выходного электрода от напряжения на этом электроде при фиксации входного тока или напряжения. Аналитическое описание характеристик можно получить из уравнения Эберса – Молла (мы, собственно, их и получили для схемы ОБ). Для конкретных режимов Т эти уравнения могут быть существенно упрощены. Так для нормального активного ненасыщенного режима в зависимости (3) исчезнут экспоненциальные зависимости, и как частный случай, получается зависимость (6). На рисунках изображены входные и выходные ВАХ для ОБ.

Iк Iэ(мА)

Uк=0

Uк>0

1,5

II I

DIэ = 0,6мА 1 Uк<0

DIк DIэ DIэ = 0,4мА DIэ

DIэ = 0,2мА 0,5

Uкк Uбэ

0,5

Режим двойной Активный режим DUэ

Инжекции

По выходным характеристикам ярко видны 2 режима работы (2 области):

1) Uк>0

2) Uк<0

Первая соответствует нормальному активному режиму при обратно – смещенном (коллекторном) p-n переходе (1 квадрат), а вторая (2 квадрат) – режиму двойной инжекции. При этом Iк резко меняет направление. По приведённым характеристикам можно определить параметры транзистора. Например,

h21Б = DIэ/DIк , h11 = DUэ/DIэ и т.д.

Для схемы с ОЭ входной управляющий сигнал – базовый ток Iб. Поэтому выходная характеристика представляет собой зависимость

Iк = ¦(Uкэ)|Iб = const.

Снимают, обычно семейство таких зависимостей при различных входных токах Iб. Входная характеристика - Iб = ¦(Uбэ) при Uкэ = const.

Iк Режим насыщения Iб

Eк/R к В

S>1

5

1,5 L (Uбн)

1мА K 4

3мА

S<1 3

 2мА

2

1мА

a 1

2,5в 3в Ек(Iк=0) Uкэ Uбэ

A 0,5  

»0,1В

Для чего нужны на практике подобные зависимости?

Как отмечалось выше, по таким зависимостям можно определить численное значение

h – параметров Т. Кроме того, расчёты электронных схем необходимо выполнять с целью обеспечения заданных параметров схемы, которые, в свою очередь, существенно зависят от режима работы транзистора. При таких расчётах необходимо знать зависимость

Uк = ¦(Iк, Iб)

и другие подобные зависимости. Рассмотрим на примере схемы с ОЭ.

Для определения этих зависимостей на выходных характеристиках строят т.н. нагрузочную зависимость (коллекторную динамическую характеристику). Из схемы видно: +Ек Uк = Ек - IкRк

Iк Rк Т.к. для данной схемы Ек и Rк = const, то зависимость

Uк является уравнением прямой линии. Для её построения

Iб  требуется найти 2 точки:

1) Пусть Iк = 0, тогда Uк = Ек

2) Создадим режим К.З по выходу

Uк = 0, тогда Iк = Ек/Rк

Т.к. зависимость линейная, то через 2 известных точки

проводим прямую, называемую нагрузочной. Она имеет

Iэ наклон (угол a) – обратно пропорционально зависящий от Rк. По нагрузочной прямой можно определить величину Uк и Iк при определённом входном токе (ток Iб). Например, при подаче Iб = 3мА получим Iк = 1мА, Uк = 3В. Если Iб имеет до 4мА, то Iк = 1,5мА, Uк = 2,5В (координата точки L).

Т.к. каждая ветвь соответствует определённому Iб, то координаты (Uк,Iк) точки пересечения этой ветви с нагрузочной прямой будет определять входные параметры каскада ОЭ. Эта точка пересечения называется рабочей точкой транзистора (точка K,

L,A,B). Т.к. при изменении Iб, рабочая точка перемещается по нагрузочной прямой, то говорят, что нагрузочная прямая представляет собой геометрическое место рабочих точек транзистора. Из рисунка видно, что крайние положения рабочей точки на прямой соответствуют точке А и точке В.

Точка А характерна тем, что Iб = 0 (p-n переход Б-Э закрыт) и транзистор работает в режиме отсечения.

Точка В характерна тем, что изменение (увеличение Iб больше Iбн) не приводит к изменению Iк. Точка В соответствует границе режима насыщения. Заштрихованная область соответствует работе Т в режиме насыщения, который характерен тем, что изменение DIб в некоторых пределах не приводит к изменению Iк (точка В неподвижна).

В таком режиме изменение Iб происходит за счёт изменения инжекционного тока Iк и этот ток создаёт избыточный заряд неосновных носителей в области базы. Чем больше величина Iб – Iбн, тем большей величины избыточный заряд находится в базе. Накопление избыточного заряда определяет С диф и с точки зрения динамики схемы, является нежелательным. Степень «избыточности» Iб характеризуется коэффициентом насыщения

S = Iб/Iбн, где S £ 1 – соответствует линейному активному режиму

S ³ 1 – насыщение Т

На участке в качестве нагрузки Т используют не только резисторы, обеспечивающие линейную зависимость линии нагрузки. Часто нагрузкой Т является также Т, включённый определённым образом и имеющий, чаще всего, тип проводимости, противоположный активному транзистору. Такая пара транзисторов называется комплиментарной парой (комплиментарное взаимодополнение). Чаще всего комплиментарные пары используются для построения схем на униполярных полупроводниках. ВАХ нагрузочного Т – нелинейная, следовательно, нагружающая линия на семействе входных характеристик активного транзистора также будет нелинейной. Это иногда позволяет получать хорошие параметры схем ЭВМ.

УНИПОЛЯРНЫЕ ТРАНЗИСТОРЫ (УТ)

Униполярными называются Т, работа которых основана на управлении либо размерами токопроводящей области (канала) либо проводимостью такой области посредством изменения напряжённости поперечно приложенного электрического поля.

Т.е. в основу работы таких Т положен ранее рассмотренный нами эффект поля.

Работа УТ основана на использовании только одного типа носителей (либо е, либо «дырок») отсюда и название «униполярный».

Существует несколько разновидностей УТ.

-И З +С На рисунке представлена структура УТ с n - каналом

Управляющее поле создаётся подачей напряжения

Канал между затвором и подножкой. Электроды И и С

в принципе обратимы. Стоком называется тот, к

которому будут двигаться канальные носители при

n + n - изменении соответствующей полярности Uси. Для n-

Полупроводник канального д.б. Uс > 0. Затвор отделён от канала тонким

 р подножка слоем изоляции. Канал, т.е. проводящий слой, может

быть создан технологическим путём, т.е. посредством

соответствующего легирования приповерхностного слоя

под затвором. Другая разновидность УТ предполагает образование каналом при подаче на затвор напряжения определённой величины полярности.

В первом случае имеем УТ со встроенным, а во втором – с индуцированным каналом.

Чтобы исключить протекание тока в цепи З, его необходимо изолировать от канала. Поэтому такие УТ называют «Т с изолированным затвором» или же «Т со структурой МДП», а т.к. Д – чаще всего окисел, то «МОП - транзистор».

Третья разновидность структуры УТ представлена на рисунке.

Затвор отделён от полупроводника не диэлектриком, а p-n переходом. Затвор – подножка.

Подавая на затвор различное напряжение (запирающее), мы получим ширину канала, а

следовательно, и его сопротивление будет модулироваться по закону изменения Uз.

И З С Такой транзистор называется полевым Т

с управляющим p-n переходом.

+ + Если контакт Ме – И (затвор – ПП) пред

р – слой ставляет собой диод Шоттки, то такой Т

называют полевым Т с барьером Шоттки.

Iс Толщина ПП (А) – фактически определяет

h – полупро ширину канала и д.б. порядка единиц М.

водник Такой ПП не имеет достаточной механи

А ческой прочности, поэтому выполняется

в виде плёнки (чаще эпитаксиальной) на

 более толстой ПП пластине – подножке.

Канал Вкратце рассмотрим особенности этих полупроводниковых структур.

ПОЛЕВЫЕ ТРАНЗИСТОРЫ С P-N ПЕРЕХОДОМ

Схема включения полевого транзистора представлена на рисунке.

На З подаётся напряжение, смещающее p-n переход в

Iс обратном направлении. Переход несимметричный

(np >> nn) и область его объёмного заряда смещена

n+ в n – область. Ток между стоком и источником проте