Навигация
Будет выбрана так, чтобы управляемые переменные находились на верхнем уровне, т.е. xi1 = +1
Матрицы планирования любого другого типа, например, 24, 25 и т.д. могут быть получены описаным выше способом.
Поскольку изменение выходной величины Y носит случайный характер, необходимо в каждой точке ![]() g (т.е. в точке с координатами, записаными в g-й строке) проводить m параллельных опытов и результаты наблюдений Y1g,Y2g,...,Ymg усреднять
g (т.е. в точке с координатами, записаными в g-й строке) проводить m параллельных опытов и результаты наблюдений Y1g,Y2g,...,Ymg усреднять
|
| (4) |
Величина m может быть любой, но не меньше m=3. Тогда эксперимент делится на m серий опытов, в каждой из которых полностью реализуется матрица планирования (т.е. эксперимент проводится в N=2n точках факторного пространства).
Одним из важнейших положений современной теории планирования эксперимента является рандомизация. План эксперимента составляется так, чтобы рандомизировать, т.е. сделать случайными те систематически действующие факторы, которые трудно поддаются учету и контролю, для того, чтобы рассматривать их как случайные величины и учитывать статистически.
Перед реализацией плана на объекте необходимо произвести рандомизацию - с помощью таблицы равномерно распределенных случайных чисел (табл.П.6) определить последовательность реализации матрицы планирования в каждой из m серий опытов. Для этого в качестве начала выбирается любое число из табл.П.6 и записывается в столбец k1 из табл.2 на место g=1. Остальные места этого столбца заполняют числа от 1 до N, следующие по порядку из табл.П.6 за выбранным начальным. Следует обращать внимание на то, чтобы числа в столбцах табл.2 не повторялись дважды. Пусть, например, при g=4 k14=8, это значит, что в первой серии испытаний точка ![]() 4 реализуется восьмой по порядку.
4 реализуется восьмой по порядку.
Аналогично рандомизируются испытания в каждой из оставшихся серий экспериментов; порядок реализации записывается в столбцах k2,k3,...,km. Результаты эксперимента в каждой из серий испытаний записываются в столбцах Y1,Y2,...,Ym.
Проверка воспроизводимости - это проверка на выполнение второй предпосылки регрессионного анализа об однородности выборочных дисперсий S2g. Задача состоит в проверке гипотезы о равенстве дисперсий s2{Y1}=s2{Y2}=...s2{YN} при экспериментах соответственно в точках ![]() 1,
1,![]() 2,...,
2,...,![]() g,...,
g,...,![]() N.
N.
Оценки дисперсий находятся по формуле
|
| (5) |
Так как все дисперсии получены по выборкам одинакового объема m, то число степеней свободы для всех дисперсий одинаково и равно
| v1 = m-1 | (6) |
Для проверки гипотезы об однородности оценок дисперсий следует пользоваться критерием Кохрена, который основан на законе распределения отношения максимальной эмперической дисперсии к сумме всех дисперсий, т.е.
|
| (7) |
Если вычисленное значение критерия G окажется меньше табличного значения Gкр, найденного для q%-ного уровня значимости, vзн = v2 = N - числа степеней свободы знаменателя (например для q=5%; vчисл = 3 - 1 = 2; vзн=8, Gкр = 0,5157, см. табл.П.5), то гипотеза об однородности дисперсий принимается. При этом всю группу дисперсий S2g можно считать оценкой S2{Y} одной и той же генеральной дисперсии воспроизводимости s2{Y}, откуда
|
| (8) |
Если проверка на воспроизводимость дала отрицательный результат, то остается признать либо невоспроизводимость эксперимента относительно управляемых переменных вследствие наличия флуктуаций неуправляемых и неконтролируемых переменных, создающих на выходе большой уровень "шума", либо наличие грубого промаха в строке, откуда взята дисперсия max{S2g}. В первом случае следует увеличить число параллельных опытов, во втором - найти грубый промах и заменить его на результат доброкачественного измерения при соответствующей комбинации факторов. Если это по каким-то причинам невозможно, то, чтобы не нарушать предпосылки использования критерия Кохрена, на место грубого промаха следует поместить среднюю арифметическую величину ![]() g данной строки.
g данной строки.
Следует также отметить, что критерий Кохрена можно применять не к любой группе выборок, а только к группе выборок одинакового объема, что как раз и имеет место при полном факторном эксперименте.
Легко заметить, что исходный план (табл.1) содержит много больше строк, чем столбцев и, следовательно, из результатов эксперимента согласно условию решения нормальных уравнений (2) можно получить дополнительную информацию, т.е. расширить модель. Безусловно, это относится к средней арифметической всего эксперимента, т.е. к отклику в базовой точке b0, для расчета которого можно ввести фиктивную переменную xод = +1 для всех строк. Оставшиеся свободными столбцы можно использовать для нахождения оценок коэффициентов при парных взаимодействиях и т.п. При этом соответствующие величины xixj, xixjxl получаются простым перемножением соответствующих столбцов исходного плана.
Тогда математическая модель объекта, получающаяся в результате ПФЭ может быть представлена в виде
| Y = b0 + b0x1 + bnxn + b12x1x2 + b(n-1)x1x2 + b123x1x2x3 + b123...nx1x2x3x3 | (9) |
Однако вследствие того, что из ограниченного числа опытов нельзя получить точные значения коэффициентов bi, а только их независимые оценки bi, вся математическая модель становится оценочной
|
| (10) |
Пример матрицы планирования, принцыпа ее реализации и последующей обработки экспериментальных данных приведен в табл.2 на базе трехфакторного эксперимента. В разделе "Матрица планирования эксперимента" включены не только относительные переменные xi, сочетание которых и является собственно настоящей матрицей планирования, ни и их парные и тройные взаимодействия, знание которых необходимо лишь на этапе обработки экспериментальных данных.
| Таблица 2 |
| Матрица планирования ПФЭ типа N=23 и обработка его результатов |
| номер g | Порядок реализации опытов | Матрица планирования эксперимента | Результаты эксперимента | Первичная | Проверка | |||||||||||||||||
| l | z0 | z1 | z2 | z3 | z4 | z5 | z6 | z7 | Yg1 | ... | Ygl | ... | Ygm |
| S2g |
| ( | |||||
| k1 | ... | kl | ... | km | x0 | x1 | x2 | x3 | x1x2 | x1x3 | x2x3 | x1x2x3 | ||||||||||
| 1 | 1 | ... | 6 | ... | 8 | + | - | - | - | + | + | + | - | |||||||||
| 2 | 7 | ... | 5 | ... | 4 | + | + | - | - | - | - | + | + | |||||||||
| 3 | 3 | ... | 7 | ... | 6 | + | - | + | - | - | + | - | + | |||||||||
| 4 | 8 | ... | 2 | ... | 7 | + | + | + | - | + | - | - | - | |||||||||
| 5 | 6 | ... | 3 | ... | 2 | + | - | - | + | + | - | - | + | |||||||||
| 6 | 4 | ... | 4 | ... | 1 | + | + | - | + | - | + | - | - | |||||||||
| 7 | 2 | ... | 1 | ... | 5 | + | - | + | + | - | - | + | - | |||||||||
| 8 | 5 | ... | 8 | ... | 3 | + | + | + | + | + | + | + | + | |||||||||
Для удобства расчетов и представления формул каждый столбец может быть представлен в виде новой переменной Zig. Тогда оценки коэффициентов уравнения регрессии легко найти по формуле
|
| (11) |
Легко заметить, что матрица планирования ![]() является ортогональной с линейно независимыми вектор-столбцами; отсюда следует диагональность матрицы нормальной системы уравнений, а следовательно, и взаимная независимость оценок коэффициентов уравнения регрессии.
является ортогональной с линейно независимыми вектор-столбцами; отсюда следует диагональность матрицы нормальной системы уравнений, а следовательно, и взаимная независимость оценок коэффициентов уравнения регрессии.
Необходимо отметить, что получаемая модель не дает членов типа x2ii и, таким образом, является неполной. В большинстве случаев это не отражается на качестве модели, так как чаще всего bii=0. Однако в случаях, когда bii¹0, модель становится неточной (неадекватной), тогда следует от ПФЭ переходить к другим принципам планирования (как правило, это случается в окрестностях частного или глобального экстремума целевой функции).
После определения оценок коэффициентов регрессии необходимо проверить гипотезу о значимости коэффициентов bi. Лучше всего это сделать в виде нуль-гипотезы, т.е. гипотезы о равенстве bi = 0. Если она подтвердилась, то коэффициент bi следует признать статистически незначимым и отбросить из искомой модели; если гипотеза не подтвердилась, то соответствующий коэффициент bi следует признать значимым и включить в модель.
Проверка гипотезы проводится с помощью t - критерия Стъюдента, который при проверка нуль-гипотезы формируется в виде
|
| (12) |
где S2{bi}- дисперсия ошибки определения коэффициента bi. При полном и дробном факторном планировании для всех i
|
| (13) |
Если вычисленная величина параметра ti превышает табличное значение tкр, найденное для q%-ного уровня значимости и vз=N(m-1) числа степеней свободы (например для q = 5%; vз = 16; tкр = 2,199, см.табл.П.2) то нуль-гипотеза отвергается и коэффициент считается незначимым и его следует отбросить, не включая в искомую модель.
Статистическая незначимость коэффициента bi может быть обусловлена следующими причинами:
уровень базового режимаПоскольку ортогональное планирование позволяет определять доверительные границы для каждого из коэффициентов регрессии в отдельности, то, если какой-либо из коэффициентов окажется незначимым, он может быть отброшен без пересчета всех остальных. После этого математическая модель объекта составляется в виде уравнения связи выходного параметра Y и переменных xi, включающего только значимые коэффициенты.
Чтобы проверить гипотезу об адекватности представления результатов эксперимента найденному уравнению связи (иными словами, чтобы проверить, насколько найденное уравнение соответствует экспериментальным результатам), достаточно оценить отклонение выходной величины Yg, предсказанное уравнением регрессии, от результатов экспериментов ![]() g в точках
g в точках ![]() факторного пространства.
факторного пространства.
Рассеяние результатов эксперимента вблизи уравнения связи, аппроксимирующего искомую функциональную зависимость, можно охарактеризовать с помощью дисперсии неадекватности s2ад, оценка которой S2ад находится по формуле
|
| (14) |
с числом степеней свободы vад = N-d, где d - число членов аппроксимирующего полинома.
Проверка адекватности состоит в выяснении соотношения между дисперсией неадекватности s2ад и дисперсией воспроизводимости s2{Y}. Если s2ад не превышает дисперсии опыта, то полученная математическая модель адекватно представляет результаты эксперимента, если же s2ад> s2{Y}, то описание считается неадекватным объекту.
Проверка гипотезы об адекватности проводится с использованием F-критерия Фишера.
Критерий Фишера позволяет проверить нуль-гипотезу о равенстве двух генеральных дисперсий s2ад и s2{Y}. В связи с тем, что самих генеральных дисперсий мы не знаем, F-критерий формируется как отношение
|
| (15) |
Если вычисленное по формуле (15) значение критерия F меньше табличного Fкр, найденного для q%-ного уровня значимости, vчисл = vад = v4 = N-d числа степеней свободы числителя и vзн = vз = N(m-1) числа степеней свободы знаменателя, то нуль-гипотеза принимается. В противном случае она отвергается и описание (модель) признается неадекватным объекту. Некоторые значения Fкр(q=5%;v4;vз) приведены в табл.П.4
В ходе работы может возникнуть ситуация, когда выборочная дисперсия неадекватности S2ад не превосходит оценки дисперсии воспроизводимости S2{Y} (т.е. когда S2ад£S2{Y}). Тогда соотношение (15) будет равно F£1 и неравенство F<Fкр выполняется для любого числа степеней свободы v4 и v3, т.е. гипотеза s2ад £s2{Y} не противоречит выборочным данным и математическая модель адекватно представляет объект.
Проверка адекватности возможна только при vад = v4 > 0. Число вариантов варьирования плана ПФЭ равно числу оцениваемых коэффициентов регрессии уравнения связи (N = d). Следовательно, не остается степеней свободы (vад = 0) для проверки нуль-гипотезы об адекватности представления экспериментальных данных выбранной формой аппроксимирующего полинома. Если же некоторые коэффициенты регрессии оказались незначимыми или ими можно пренебречь в силу их малости, то число членов проверяемого уравнения в этом случае будет меньше числа вариантов варьирования (d<N), и одна или несколько степеней свободы (vад>0) останется для проверки гипотезы адекватности.
Если гипотеза адекватности отвергается, то модель признается неадекватной экспериментальным данным. Неадекватность модели не означает ее неправильности! Неадекватность модели может означать, что не весь перечень влияющих факторов был принят во внимание, или что необходимо перейти к более сложной форме уравнения связи, или выбрать другой шаг варьирования по одному или нескольким факторам и т.п. Однако все достижения неадекватной модели: отсев незначимых факторов, оценка дисперсии эксперимента и др. остаются в силе.
Пример 1. Методом ПФЭ найти математическую модель процесса напыления резисторов.
После консультации с экспертами и некоторых предварительных исследований было определено, что на величину сопротивления напыляемых резисторов могут оказывать влияние следующие факторы:
Состояние испарителя - "чистое", т.е. порошок для напыления сыпется в стакан испарителя впервые после промывки его сторон, или "грязное", т.е. порошок сыпется в испаритель, в котором осталось некоторое его количество от предыдущего цикла напыления; обозначим этот фактор как x1, причем величина x1 = +1соответствует "чистому", а величина x1 = -1 соответствует "грязному" состоянию испарителя; Температура подогрева подложки x2, причем x2 = +1 соответствует верхней допустимой по техпроцессу температуре, а x2 = -1 - нижней; Температура испарителя x3, причем x3 = +1 соответствует верхней допустимой по техпроцессу температуре, а х3 = -1 - нижней.План эксперимента, его пятикратная реализация с учетом рандомизации и первичная обработка результатов представлена в таблице.
| номер g | Циклы | z0 | z1 | z2 | z3 | z4 | z5 | z6 | z7 | Результаты, кOм | Обработка | Адекватность |
| ||||||||||
|
| S2g |
| ( | ||||||||||||||||||||
| k1 | k2 | k3 | k4 | k5 | x0 | x1 | x2 | x3 | x1x2 | x1x3 | x2x3 | x1x2x3 | Yg1 | Yg2 | Yg3 | Yg4 | Yg5 |
| |||||
| 1 | 4 | 2 | 3 | 6 | 8 | + | - | - | - | + | + | + | - | 11,4 | 10,5 | 13,8 | 14,0 | 12,1 | 12,36 | 2,303 | 12,10 | 0,0676 | |
| 2 | 3 | 3 | 6 | 2 | 5 | + | + | - | - | - | - | + | + | 18,1 | 17,4 | 15,2 | 16,8 | 19,2 | 17,34 | 2,228 | 17,08 | 0,0676 |
|
| 3 | 8 | 6 | 2 | 4 | 1 | + | - | + | - | - | + | - | + | 10,8 | 9,3 | 11,6 | 12,1 | 9,8 | 10,72 | 1,387 | 10,98 | 0,0676 |
|
| 4 | 6 | 1 | 7 | 1 | 6 | + | + | + | - | + | - | - | - | 18,8 | 29,6 | 22,0 | 22,8 | 20,7 | 21,38 | 2,752 | 21,64 | 0,0676 |
|
| 5 | 5 | 8 | 1 | 3 | 4 | + | - | - | + | + | - | - | + | 12,9 | 12,8 | 13,6 | 15,2 | 14,0 | 13,70 | 0,950 | 13,98 | 0,0784 |
|
| 6 | 2 | 5 | 5 | 7 | 2 | + | + | - | + | - | + | - | - | 12,0 | 11,6 | 14,2 | 13,4 | 12,5 | 12,74 | 1,118 | 13,00 | 0,0676 |
|
| 7 | 1 | 7 | 4 | 8 | 7 | + | - | + | + | - | - | + | - | 15,1 | 14,8 | 16,8 | 18,1 | 17,0 | 16,36 | 1,913 | 16,10 | 0,0676 |
|
| 8 | 7 | 4 | 8 | 5 | 3 | + | + | + | + | + | + | + | + | 13,5 | 11,9 | 14,3 | 17,0 | 16,2 | 14,58 | 4,227 | 14,32 | 0,0676 |
|
| å | 119,18 | 16,878 | - | 0,5410 |
| ||||||||||||||||||
При первичной обработке результатов экспериментов пользуемся формулами (4) и (5), а затем проверяем воспроизводимость опытов по (7)
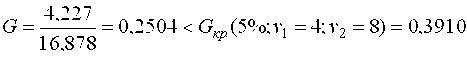
Таким образом, подтверждена воспроизводимость опытов (отсутствие в данных грубых промахов), что позволяет, в свою очередь, найти среднюю дисперсию строчных выборок (дисперсию опытов) по (8)
|
| C | v3 = 8·(5-1) = 32 степенями свободы |
Оценки коэффициентов уравнения регрессии ищутся по формуле (11)
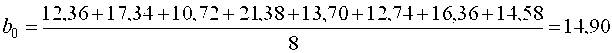
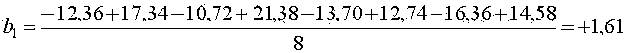
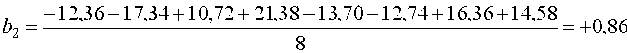
и т.д. Аналогично находим b3 = -0,55; b12 = +0,61; b13 = -2,30; b23 = +0,26; b123 = -0,81
Проверяем значимость оценок коэффициентов по критерию Стьюдента по формуле (12), предварительно найдя дисперсию оценок по формуле (13)
|
| ; |
| |||||
| Тогда |
| ; |
| ; |
| ||
| далее аналогично | t12 = 2,602 | ; | t13 = 9,812 | ; | t23 = 1,109 | ; | t123 = 3,455 |
Табличное значение критерия ti (табл.П.2) tкр(5%;v3=32) = 2,046, поэтому все найденные оценки коэффициентов, кроме b23, признаются значимыми и должны войти в модель
![]() = 14,90 + 1,61x1 + 0,86x2 -0,55x3 + 0,61x1x2 -2,30x1x3 - 0,81x1x2x3
= 14,90 + 1,61x1 + 0,86x2 -0,55x3 + 0,61x1x2 -2,30x1x3 - 0,81x1x2x3
Для определения дисперсии адекватности по формуле (14) необходимо сначала найти числовые значения модели ![]() g для каждой g-ой строки матрицы планирования, а затем подсчитать сумму квадратов разностей между модельным значением и средним арифметическим
g для каждой g-ой строки матрицы планирования, а затем подсчитать сумму квадратов разностей между модельным значением и средним арифметическим ![]() g той же строки
g той же строки
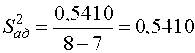
Тогда критерий Фишера (15) дает
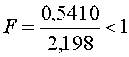
что доказывает адекватность найденной модели. Ее можно использовать для управления технологическим процессом испытания резисторов
Похожие работы
... и человеку. Как видите, немалую роль в решении проблемы сохранения жизни на Земле играет математика с ее методом математического моделирования. Итак, при объяснении метода математического моделирования и его применения к решению экологических задач реализуется практическая направленность обучения, поскольку математический метод применяется к разрешению жизненной, практической, глобальной (!) ...
... целом как сложной системы в различных условиях. Вычислительные эксперименты с математическими моделями дают исходные данные для оценки показателей эффективности объекта. Поэтому математическое моделирование как методология организации научной экспертизы крупных проблем незаменимо при проработке народнохозяйственных решений. (В первую очередь это относится к моделированию экономических систем[6]). ...
... вопросы должны быть получены в ходе маркетинговых и проектно-изыскательских работ на фазе проектирования спортивных сооружений. И уже на этой стадии в процесс активно включаются экономико-математические методы, задействуется существующий аппарат математического моделирования и прогнозирования. Данные методы и расчеты совершенно необходимы для определения: сроков окупаемости отдельных предприятии ...
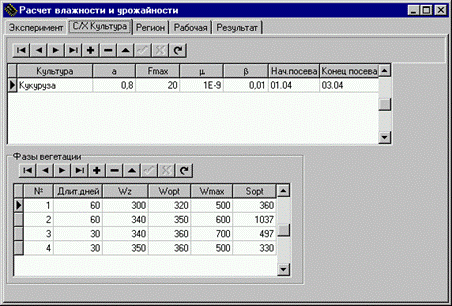
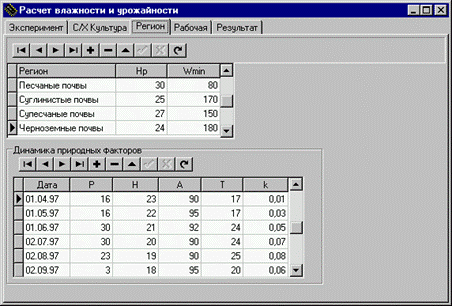
... и точных математических методов идентификации и прогноза, более интеллектуального, эффективного и гибкого математического и программного обеспечения, эффективных критериев адекватности и устойчивости моделей, а также технологии моделирования. С этих позиций рассматривается модель расчета влажности почвы с учетом накапливаемой биомассы и прогнозирования урожайности сельхозкультур по заданной ( ...
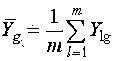
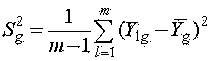
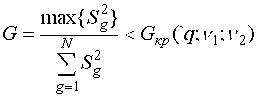
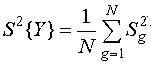
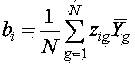
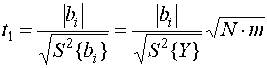
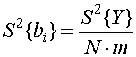
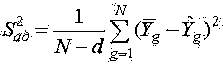
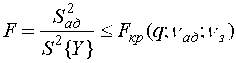
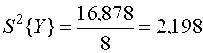
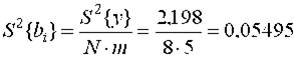
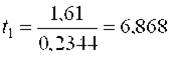
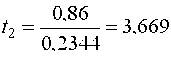
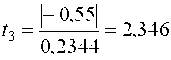


0 комментариев