Навигация
Дробный факторный эксперимент
2. Дробный факторный эксперимент
Полный факторный эксперимент целесообразно использовать при сравнительно небольшом числе независимых факторов (обычно не больше 5), в противном случае число вариантов варьирования N = 2n становится непомерно большим и реализация эксперимента затрудняется. В то же время в большинстве практических задач взаимодействия внешних порядков, начиная с третьего (а то и второго), отсутствуют или пренебрежимо малы, вследствие чего излишне много степеней свободы остается на проверку гипотезы адекватности. Если заранее пренебречь взаимодействиями высших порядков, то имеется возможность получить математическую модель при меньшем числу опытов, реализовав не весь план ДФЭ, а только его часть (дробную реплику).
Эксперимент, реализующий часть (дробную реплику) полного факторного эксперимента, называется дробным факторным экспериментом (ДФЭ). ДФЭ позволяет получить приближение искомой функциональной зависимости Y = f(X1,...,Xn) в некоторой небольшой окрестности точки базового режима при минимуме опытов.
Так, для решения трехфакторной задачи можно ограничиться четырьмя вариантами (N = 4), если в планировании ПФЭ типа 22 произведение x1x2 приравнять к третьей независимой переменной x3. Такое планирование, представленное матрицей табл 3, позволяет оценить свободный член b0 и три коэффициента регрессии при линейных членах b1,b2,b3 (из четырех опытов нельзя получить более четырех коэффициентов).
| Таблица 3 | ||||||||
| Полуреплика от ПФЭ типа 23 (планирование типа 23-1) | ||||||||
| g | z0 | z1 | z2 | z3 | z4 | z5 | z6 | z7 |
| x0 | x1 | x2 | x3 | x1x2 | x1x3 | x2x3 | x1x2x3 | |
| 1 | + | - | - | + | + | - | - | + |
| 2 | + | + | - | - | - | - | + | + |
| 3 | + | - | + | - | - | + | - | + |
| 4 | + | + | + | + | + | + | + | + |
Применение ДФЭ всегда связано со смешиванием, т.е. совместной оценкой нескольких коэффициентов уравнения связи. В нашем примере, если коэффициенты регрессии bij при парных произведениях отличны от нуля, то каждый из найденных коэффициентов будет оценкой двух теоретических коэффициентов:
b0 ® b0 + b123 ; b2 ® b2 + b13 ;
b1 ® b1 + b23 ; b3 ® b3 + b12 .
Действительно, указанные коэффициенты в таком планировании не могут быть найдены раздельно, поскольку столбцы матрицы для линейных членов и парных произведений совпадают (полностью скоррелированы). Рассмотренный план ДФЭ представляет половину плана ДФЭ типа 23 и называется "полурепликой" от ПФЭ типа 23 или планированием типа N = 23-1.
При большом числе переменных можно построить дробные реплики высокой степени дробности (1/4, 1/8, 1/16 и т.д.). Дробная реплика обозначается через 2n-p, если p переменных приравнены к соответствующим произведениям переменных.
Для правильного планирования ДФЭ необходимо использовать все полученные ранее сведения об объекте теоретического и интуитивного характера и выделить из них те переменные и произведения переменных, влияние которых на процесс минимально. При этом смешивание нужно производить так, чтобы основные оценки b0,b1,...,bn были смешаны с взаимодействиями, о которых заранее известно, что они не оказывают влияния на объект. Следовательно, произвольное разбиение матрицы планирования 23 на две части выделения полуреплики типа 23-1 недопустимо.
Генерирующее соотношение служит для построения дробной реплики. Так, в рассмотренном планировании 23-1 мы задавали полуреплику типа 23 с помощью генерирующего соотношения x3 = x1x2.
Определяющим контрастом (ОК) называется соотношение, задающее элемент первого столбца матрицы планирования для фиктивной переменной (все они равны 1). Выражение ОК в нашем примере получается умножением левой и правой частей приведенного генерирующего соотношения на его левую часть x3
1 = x1x2x3,
так как всегда x2ig = 1.
Знание ОК позволяет определить всю систему совместных оценок не изучая матрицу планирования ДФЭ. Соотношения, задающие эти оценки, можно найти, последовательно перемножив независимые переменные на ОК
x1 = x2x3 ; x2 = x1x3 ; x3 = x1x2.
Отсюда легко находим смешиваемые теоретические коэффициенты регрессии и их оценки
b1 ® b1 + b23 ; b2 ® b2 + b13 ; b3 ® b3 + b12 .
Разрешающая способность дробных реплик определяется генерирующими соотношениями. Она тем выше, чем выше порядок взаимодействий, с которыми смешаны линейные коэффициенты, и увеличивается с ростом числа независимых переменных.
Для четверти реплики в пятифакторном планировании типа 25-2 могут быть заданы, например генерирующее соотношение
x4 = x1x2x3 ; x5 = x1x2
заранее полагая, что b123 = b12 = 0, т.е. что пара x1x2 и тройка x1x2x3 не дает значимого эффекта взаимодействия. Определяющими контрастами для этой четверть-реплики согласно вышеприведенным правилам будут соотношения
1 = x1x2x3x4 ; 1 = x1x2x5.
Если у дробной реплики имеются два и более определяющих контраста, их необходимо перемножить между собой, используя все возможные комбинации. В случае четвертьреплики получается одна комбинация
1 = x3x4x5
Обобщающий определяющий контраст, построенный на основе всех полученных определяющих контрастов, полностью характеризует разрешающую способность реплик высокой степени дробности
1 = x1x2x3x4 = x1x2x5 = x3x4x5.
Совместные оценки здесь будут определяться соответствиями
x0 = x1x2x3x4 = x1x2x5 = x3x4x5 ;
x1 = x2x3x4 = x2x5 = x1x3x4x5 ;
x2 = x1x3x4 = x1x5 = x2x3x4x5 ;
x3 = x1x2x4 = x1x2x3x5 =x4x5 ;
x4 = x1x2x3 = x1x2x4x5 =x3x5 ;
x5 = x1x2x3x4x5 = x1x2 = x3x4 ;
x1x3 = x2x4 = x2x3x5 = x1x4x5 ;
x2x3 = x1x4 = x1x3x5 =x2x4x5 ;
Эти соотношения позволяют установить, оценкой каких теоретических коэффициентов является тот или иной коэффициент регрессии, полученный при обработке результатов эксперимента
b0 = b0 + b1234 + b125 + b345 ;
b1 = b1 + b234 + b25 + b1345 ;
b2 = b2 + b134 + b15 + b2345 ;
b3 = b3 + b124 + b1235 + b45 ;
b4 = b4 + b123 + b1245 + b35 ;
b5 = b5 + b12345 + b12 + b34 ;
b13 = b13 + b24 + b235 + b145 ;
b23 = b23 + b14 + b135 + b245 ;
Разрешающая способность этой четверти реплики невысокая, так как все линейные коэффициенты смешаны с парными взаимодействиями. Матрица планирования такой четверти реплики представлена в табл.4.
Следует иметь в виду, что ДФЭ всегда можно дополнить до ПФЭ, реализовав недостающие дробные реплики.
Вся дальнейшая работа по реализации матрицы планирования ДФЭ, проверке воспроизводимости полученных результатов, определению оценок коэффициентов регрессии и их значимости, проверке адекватности полученной математической модели не отличается от соответствующих процедур в ПФЭ.
Таблица 4
Четверть реплики от ПФЭ типа 25 (планирование типа 25-2)
| g | z0 | z1 | z2 | z3 | z4 | z5 | z6 | z7 | z8 | z9 | z10 | z11 | z12 | z13 | z14 | z15 | z16 | z17 | z18 | z19 | z20 | z21 | z22 | z23 | Z24 | z25 | z26 | z27 | z28 | z29 | z30 | z31 |
| x0 | x1 | x2 | x3 | x4 | x5 | x1x2 | x1x3 | x1x4 | x1x5 | x2x3 | x2x4 | x2x5 | x3x4 | x3x5 | x4x5 | x1x2x3 | x1x2x4 | x1x2x5 | x1x3x4 | x1x3x5 | x1x4x5 | x2x3x4 | x2x3x5 | x2x4x5 | x3x4x5 | x1x2x3x4 | x1x2x3x5 | x1x2x4x5 | x1x3x4x5 | x2x3x4x5 | x1x2x3x4x5 | |
| 1 | + | - | - | - | - | + | + | + | + | - | + | + | - | + | - | - | - | - | + | - | + | + | - | + | + | + | + | - | - | - | - | + |
| 2 | + | + | - | - | + | - | - | - | + | - | + | - | + | - | + | - | + | - | + | - | + | - | + | - | + | + | + | - | + | + | - | - |
| 3 | + | - | + | - | + | - | - | + | - | + | - | + | - | - | + | - | + | - | + | + | - | + | - | + | - | + | + | - | + | - | + | - |
| 4 | + | + | + | - | - | + | + | - | - | + | - | - | + | + | - | - | - | - | + | + | - | - | + | - | - | + | + | - | - | + | + | + |
| 5 | + | - | - | + | + | + | + | - | - | - | - | - | - | + | + | + | + | + | + | - | - | - | - | - | - | + | + | + | + | - | - | + |
| 6 | + | + | - | + | - | - | - | + | - | - | - | + | + | - | - | + | - | + | + | - | - | + | + | + | - | + | + | + | - | + | - | - |
| 7 | + | - | + | + | - | - | - | - | + | + | + | - | - | - | - | + | - | + | + | + | + | - | - | - | + | + | + | + | - | - | + | - |
| 8 | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + |
Пример 2. Методом ДФЭ найти математическую модель процесса напыления резисторов.
Воспользуемся результатами Примера 1 и положим в качестве генерирующего соотношения равениство x1 = x2x3 (т.к. b23 = 0). Тогда матрица планирования и результаты эксперимента (опуская промежуточные данные) будут выглядеть так
| g | x0 | x1 | x2 | x3 |
| S2g |
| ( |
| 1 | + | + | - | - | 17,34 | 2,228 | 17,41 | 0,0049 |
| 2 | + | - | + | - | 10,72 | 1,387 | 10,77 | 0,0025 |
| 3 | + | - | - | + | 13,70 | 0,950 | 13,65 | 0,0025 |
| 4 | + | + | + | + | 14,58 | 4,227 | 14,53 | 0,0025 |
Проверим воспроизводимость опытов
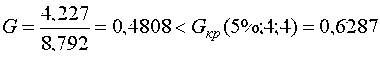
откуда следует, что результаты опытов получены правильно, дисперсия строчных выборок равна S2{y} = 8,792 / 4 = 2,198 с числом степеней свободы v3 = 4·4 = 16.
Оценки коэффициентов уравнения регрессии
|
| ; |
|
аналогично b2 = -1,44; b3 = 0,05.
Проверка значимости полученных оценок начинается с определения их СКО
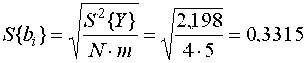
откуда
|
| ; |
| ; |
|
Табличные значения критерия tкр(5%;16) = 2,131, следовательно, модель найдена в виде
![]() = 14,09 + 1,88x1 - 1,44x2.
= 14,09 + 1,88x1 - 1,44x2.
Проверка адекватности модели дает
|
| , откуда |
| , |
т.е. модель признается адекватной экспериментальным данным.
Сравнение моделей примера 1 и примера 2 показывает, что они имеют совершенно разный вид, а по некоторым факторам - противоположные по смыслу оценки коэффициентов. Отсюда можно сделать несколько общих выводов и рекомендаций (без подробного обоснования), пригодных для использования в рамках теории планирования экспериментов:
по одним и тем же экспериментальным данным можно построить несколько математических моделей, каждая из которых будет адекватна для своего набора оценок коэффициентов регрессии; из всех моделей наилучшей признается та, у которой меньше членов и меньше критерий Фишера (или, если угодно, меньше дисперсия адекватности); при большом числе факторов работу по математическому моделированию следует начинать с ДФЭ возможно большей дробности. Если модель получилась неадекватной, ее всегда можно достроить до следующей реплики вплоть до ПФЭ. Это сэкономит количество опытов, время, затраты и т.п.Заключение.
Применение описанных выше методов математического моделирования полностью оправдало себя в условиях с небольшим числом факторов. Но при очень большом числе факторов и привлечение их к составлению математического описания исследуемого объекта методами ПФЭ или ДФЭ может потребовать увеличения объема экспериментальной работы, что редко может выполняться из-за экономических, технологических и прочих ограничений. Таким образом, возникает необходимость в предварительном отсеивании несущественных и выделении тех факторов процесса, которые оказывают наиболее заметное влияние на целевую функцию. Другим существенным затруднением для применения ПФЭ или ДФЭ в производственных условиях является метод получения оценок коэффициентов регрессии. Оценки вида (11) считаются оптимальными в смысле эффективности (минимума дисперсии), поскольку их вычисление базируется на методе наименьших квадратов, однако предварительным условием такой оптимальности являются требования независимости факторов, ортогональности и симметричности плана эксперимента, а также требование равенства дисперсий условных распределений плотности вероятности f(y/xk). В свою очередь симметричность плана требует равного количества наблюдений, соответствующих положительным и отрицательным значениям k-го фактора.
На практике в производственных условиях требования симметричности плана и равенства дисперсий условных распределений плотности вероятности f(y/xk) эксперимента, как правило, нарушаются, особенно в случаях, когда исследователь пытается построить модель по результатам, зафиксированными для случайной системы комбинаций производственных факторов. При этом всегда имеется выбор: либо нарушить одно из требований факторного анализа, либо потерять часть информации, пытаясь выбрать из нее только то, что согласуется с правилами ведения ПФЭ (ДФЭ).
Похожие работы
... и человеку. Как видите, немалую роль в решении проблемы сохранения жизни на Земле играет математика с ее методом математического моделирования. Итак, при объяснении метода математического моделирования и его применения к решению экологических задач реализуется практическая направленность обучения, поскольку математический метод применяется к разрешению жизненной, практической, глобальной (!) ...
... целом как сложной системы в различных условиях. Вычислительные эксперименты с математическими моделями дают исходные данные для оценки показателей эффективности объекта. Поэтому математическое моделирование как методология организации научной экспертизы крупных проблем незаменимо при проработке народнохозяйственных решений. (В первую очередь это относится к моделированию экономических систем[6]). ...
... вопросы должны быть получены в ходе маркетинговых и проектно-изыскательских работ на фазе проектирования спортивных сооружений. И уже на этой стадии в процесс активно включаются экономико-математические методы, задействуется существующий аппарат математического моделирования и прогнозирования. Данные методы и расчеты совершенно необходимы для определения: сроков окупаемости отдельных предприятии ...
... и точных математических методов идентификации и прогноза, более интеллектуального, эффективного и гибкого математического и программного обеспечения, эффективных критериев адекватности и устойчивости моделей, а также технологии моделирования. С этих позиций рассматривается модель расчета влажности почвы с учетом накапливаемой биомассы и прогнозирования урожайности сельхозкультур по заданной ( ...
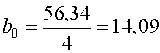
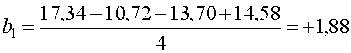
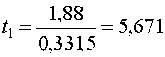
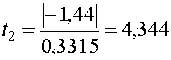
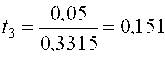
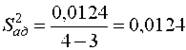
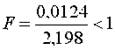


0 комментариев