Навигация
Определение силы действующей на вал
8999
знаков
1
таблица
47
изображений
2.3 Определение силы действующей на вал
По формуле [1, с 136, ф (7.31)]:
(2.15)
Н.
Расчет зубчатых колес редуктора
Исходные данные:
Передаваемая мощность – Р =2,7 кВт.
Вращающий момент на ведущем валу – Т2 =103,5 Нм.
Вращающий момент на ведомом валу – Т3 =500 Нм.
Частота вращения ведущего вала – n2=250 об/мин.
Частота вращения ведомого вала – n3=50 об/мин.
Угловая скорость ведущего вала – 2=26,2 рад/с.
Передаточное число – U2=5.
3.1 Выбор материала колес
Для шестерни примем сталь 40Х улучшенную с твердостью НВ 270; для колеса сталь 40Х улучшенной твердостью НВ 245.
Допускаемое контактные напряжения по формуле [1, с 33, ф (3.9)]:
(3.1)
где Hlimb – предел контактной выносливости при базовом цикле, значения по таблице 3.2 [1, с 34];
КHL – коэффициент долговечности, при длительной эксплуатации КHL=1;
[SH] – коэффициент безопасности, [SH]=1,15;
Hlimb=2HB+70=2·245+70=560 MПа.
МПа.
3.2
Определение
геометрических
параметров
конической
передачи
Внешний делительный диаметр колеса, по формуле [1, с 49, ф (3.29)]:
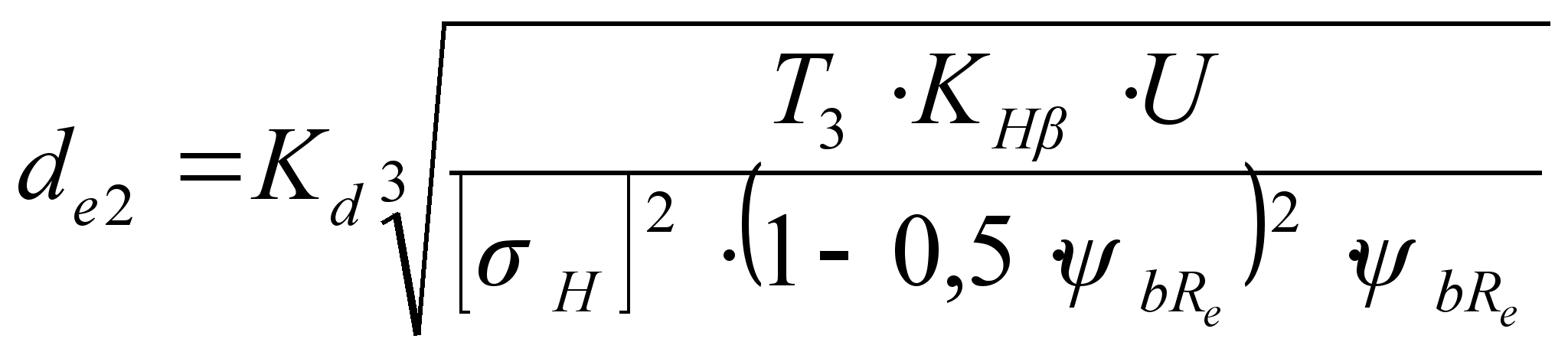(3.2)
где Т3 – вращающий момент III вала, Т3=500 Нм;
KHβ – коэффициент при консольном расположении шестерни 1,35;
U – передаточное число, U=5;
ψbRe – коэффициент ширины венца по отношению к внешнему конусному расстоянию, ψbRe=0,285;
Кd –для прямозубых передач Кd = 99
мм,
Принимаем по ГОСТ 1289-76 ближайшее стандартное значение de2=400 мм.
Примем число зубьев шестерни z1=25,
Тогда, по формуле
(3.3)
Внешний окружной модуль, по формуле:
(3.4)
мм.
Углы делительных конусов:
(3.5)
(3.6)
Внешнее конусное расстояние Re:
(3.7)
мм.
Дина зуба b
(3.8)
мм,
Принимаем b=60 мм.
Внешний делительный диаметр шестерни, по формуле:
de1=mez1 (3.9)
de1=mez1=3,225=80 мм.
Средний делительный диаметр шестерни
d1=2(Re-0,5b)sin (3.10)
d1=2(203,96-0,560)sin11є19’=68,3
мм.
Внешние диаметры шестерни и колеса (по вершинам зубьев):
daei=dei+2mecosi(3.11)
dae1=80+23,2cos11є19’=86,3 мм
dae2=400+23,2cos78є41’=401,3 мм.
Средний окружной модуль
(3.12)
мм.
Коэффициент ширины шестерни по среднему диаметру
(3.13)
Средняя окружная скорость колес:
(3.14)
м/с.
Для конических колес назначаем 9-ю степень точности.
3.3 Проверка по контактным напряжениям
Для проверки контактных напряжений определяем коэффициент нагрузки:
KH=KHβKHαKHV (3.15)
где KH
– коэффициент,
учитывающий
распределение
нагрузки по
длине зуба, при Ψbd=0,6
при консольном
расположении
колес и твердости
HB
Похожие работы
... на 5 - 10 мм меньше длины ступицы колеса Lст, Lшп = L ст - (5 - 10). Длину ступицы принимают [5, ñ.30] в зависимости от диаметра d вала под ступицей: для цилиндрической передачи Lст = (1-1,5) · d; для конической передачи Lст = (1-1,2) · d. Длина шпонки Lшп’ = Lст - (5 - 10) = 75 – 12 = 63 . Выбираем Lшп = 63. Шпонка 20 х 12 х 63 по ГОСТ 23360 – 78. Напряжение смятия узких граней шпонки не ...
... поверхностях зуба, мкм; Rz80 – шероховатость на боковых поверхностях шпоночного паза в центральном отверстии, мкм; Rz40 – шероховатость на дне шпоночного паза, мкм. 2.4 Разработка технологического процесса изготовления конического зубчатого колеса 2.4.1 Выбор заготовки и способа ее получения Для изготовления данной детали используется сталь 18 ХГТ Характеристика стали 18ХГТ Марка ...
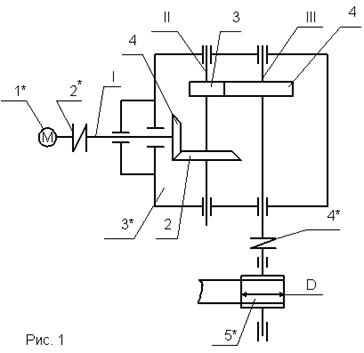
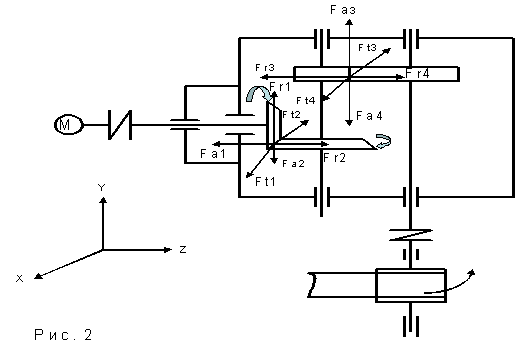
... являются основой для его дальнейшей конструкторской работы, а также для выполнения курсовых проектов по специальным дисциплинам и дипломного проекта. 1. Описание редуктора и принципа его работы В данной работе рассматривается главный редуктор вертолета. Входная коническая ступень. Вторая ступень - цилиндрическая. Редуктор предназначен для понижения оборотов и повышения крутящего момента на ...
... колес (цилиндрические, конические, коническо-цилиндрические и т.д.); относительному расположению валов редуктора в пространстве (горизонтальные, вертикальные); особенностям кинематической схемы (развернутая, соосная, с раздвоенной ступенью и т.д.). Конические редукторы применяют для передачи движения между валами, оси которых пересекаются обычно под углом 90. Передачи с углами, отличными от 90 , ...
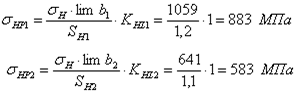
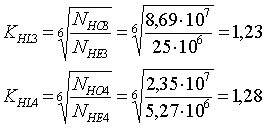
0 комментариев