Навигация
Модель отказов воздушной линии электропередач
1.3. Модель отказов воздушной линии электропередач
ЛЭП рассмотрим как элемент условно состоящий из двух последовательно соединенных элементов. В одном из которых может появиться внезапный отказ, а в другом постепенный. Вероятность безотказной работы представим как произведение вероятности двух независимых событий соединенных последовательно отностительно надежности.
РЛЭП(t)=Рв(t)*Ри(t).
Дальнейший расчет проведем как и для трансформатора. Статистические данные приведенные в таблице 11 приведены к единичной длине 1 км, как для внезапных и постепенных отказов.
Таблица 11
Статистический ряд внезапных и постепенных отказов для ЛЭП
| X, г | X, г | X, г | Y, г | Y, г | Y, г |
| 174,11 | 203,04 | 179,13 | 309,12 | 326,04 | 343,86 |
| 180,83 | 41213 | 187,67 | 316,75 | 334,17 | 351,59 |
| 189,38 | 208,17 | 194,54 | 324,5 | 341,94 | 313,62 |
| 201,33 | 177,41 | 211,58 | 332,25 | 349,68 | 321,37 |
| 206,46 | 185,96 | 196,21 | 340,02 | 312,08 | 329,12 |
| 175,72 | 192,79 | 213,29 | 347,75 | 319,82 | 338,01 |
| 184,25 | 204,75 | 197,92 | 310,54 | 327,58 | 345,78 |
| 191,08 | 209,88 | 215,67 | 318,29 | 336,09 | 363,25 |
| Т | l | Yср | Dt | ||
| 1904 | 0,00052523 | 331 | 10 |
В теории надежности в качестве основного распределения времени безотказной работы при внезапных отказах ЛЭП принимается показательное распределение:
![]()
Постепенные отказы ЛЭП происходят в основном по причине износа изоляции. Износ можно описать законом распределения Вейбула-Гниденко.
![]()
где t0 — порог чувствительности, то есть элемент гарантировано не откажет, в интервале времени от 0 до t0 может быть равно нулю. Тогда окончательно имеем:
![]() PЛЭП(t) = e-lt×e-ct=.
PЛЭП(t) = e-lt×e-ct=.
Параметр показательного закона l находим по формуле:
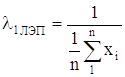
где хср— среднеее значение наработок на отказ.
Среднее время безотказной работы определим по формуле
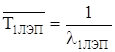
Оценим параметры распределения Вейбула-Гниденко. Для этого вычислим среднеее значение наработки на отказ
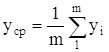
Разобьем выборку y на интервалы, которые выберем по формуле
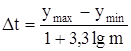
Подсчитаем сколько отказов попало в каждый из полученных интервалов
Таблица 12
| интервалы | 1 | 2 | 3 | 4 | 5 | 6 |
| мин | 309,12 | 318,86 | 328,61 | 338,35 | 348,10 | 357,84 |
| макс | 319 | 329 | 338 | 348 | 358 | 368 |
| 1 | 309,12 | 316,75 | 324,5 | 332,25 | 340,02 | 347,75 |
| 2 | 310,54 | 318,29 | 326,04 | 334,17 | 341,94 | 349,68 |
| 3 | 312,08 | 319,82 | 327,58 | 336,09 | 343,86 | 351,59 |
| 4 | 313,62 | 321,37 | 329,12 | 338,01 | 345,78 | 363,25 |
| Yicp | 311 | 319 | 327 | 335 | 343 | 353 |
| pi | 0,1666666 | 0,1666666 | 0,1666666 | 0,16667 | 0,16667 | 0,16667 |
| D | s | n | 1/a | C | T | l |
| 199 | 14 | 0,0425237 | 0,035 | 5,7E-73 | 331 | 0,00302 |
Отностительную частоту событий определяем по формуле
pi= mi/m.
Определим среднее значение для каждого интервала
![]()
Вычислим значение дисперсии D по формуле:
![]()
Определим среднеквадратичное отклонение:
![]() .
.
Вычислим коэффициент вариации по формуле:
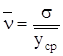 .
.
По номограмме находим значение параметра формы 1/a=0,36. По найденным значениям вычислим параметр масштаба С распределения Вейбула-Гниденко :
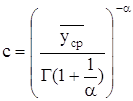
Г(1,36)=0,8902
Среднее время безотказной работы для распределения Вейбула-Гниденко определим по формуле
![]() ;
;
l2ЛЭП=1/Т2ЛЭП
В таблице 13 представлен статистический ряд восстановления отказов ЛЭП.
Интенсивность восстановления определим по формуле (1.16)
Вероятность восстановления ЛЭП определяется по формуле
Рвос.ЛЭП=1-е-m.
Таблица 13
Статистический ряд восстановления внезапных и постепенных отказов ЛЭП
| восстановление | |||
| 7,1 | 9,2 | 11,3 | 13,4 |
| 8,9 | 10,9 | 13 | 8,6 |
| 10,7 | 12,7 | 8,1 | 10,3 |
| 12,3 | 4,8 | 9,9 | 12,1 |
| 4,5 | 9,6 | 11,7 | 18,8 |
| Т= | 10,395 | m= | 0,0962 |
Результаты расчетов по приведенным выше формулам сведены в табл.11,12,13.
1.4. Модель отказов и восстановления для разъединителейПредставим разъединитель как элемент состоящий из одного элемента с внезапным отказом, с показательным законом распределения наработки на отказ (1,1). Статистический ряд представлен в таблице 14, 15 наработок на отказ и времени восстановления.
Параметр показательного закона l находим по формуле:
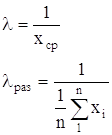
где хср— среднеее значение наработок на отказ.
Среднее время безотказной работы определим по формуле
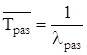
Таблица 14
Статистический ряд внезапных отказов разъединителей
| X, г | X, г | X, г | X, г |
| 6,64 | 7,40 | 6,68 | 7,13 |
| 7,06 | 7,17 | 7,44 | 7,06 |
| 6,86 | 7,12 | 7,20 | 7,22 |
| 7,20 | 6,98 | 6,83 | 7,11 |
| 6,79 | 6,83 | 7,24 | 7,48 |
| Т=7 | l=0,14143 | ||
Интенсивность восстановления определим по формуле (1.16) ![]()
Вероятность восстановления разъединителей определяется:
Рвос.раз=1-е-m.
Таблица 15
Статистический ряд времени восстановления разъединителей
| восстановление | |||
| 8,3 | 6 | 6,2 | 7 |
| 7,5 | 8 | 8,3 | 7,2 |
| 9,1 | 9,2 | 10,9 | 9 |
| 6,8 | 10,4 | 9,4 | 8,1 |
| 10,1 | 7,1 | 8,5 | 6,1 |
| Т=8,16 | m=0,12255 | ||
Результаты расчетов по приведенным выше формулам сведены в табл.14,15.
1.6. Модель отказов и восстановления для отделителей и короткозамыкателейДля отделителей и короткозамыкателей составим модель аналогичную разъединителям и проведем подобный расчет. Исходные данные и результаты расчета сведем в таблицу 16,17,18,19.
Таблица 16
Статистический ряд внезапных отказов отделителей
| X, ч | X, ч | X, ч | X, ч |
| 31377 | 35695 | 31623 | 34179 |
| 33786 | 34416 | 35974 | 33762 |
| 32653 | 34130 | 34558 | 34679 |
| 34579 | 33325 | 32455 | 34091 |
| 32231 | 32471 | 34825 | 36149 |
| Т=33848 | l=3E-05 | ||
Таблица 17
Статистический ряд времени восстановления отделителей
|
| восстановление |
| |
| 8,1 | 5,9 | 6,1 | 6,9 |
| 7,4 | 7,8 | 8,1 | 7,1 |
| 8,9 | 9,0 | 10,6 | 8,8 |
| 6,7 | 10,2 | 9,2 | 7,9 |
| 9,9 | 7,0 | 8,3 | 6,0 |
| Т=7,98933 | m=0,12517 | ||
Таблица 18
Статистический ряд внезапных отказов короткозамыкателей
| X, ч | X, ч | X, ч | X, ч |
| 32430 | 36893 | 32685 | 35326 |
| 34920 | 35570 | 37181 | 34895 |
| 33749 | 35275 | 35718 | 35842 |
| 35739 | 34443 | 33544 | 35235 |
| 33312 | 33560 | 35993 | 37362 |
| Т= | 34984 | l= | 2,9E-05 |
Таблица 19
Статистический ряд времени восстановления короткозамыкателей
| восстановление | |||
| 8,3 | 6 | 6,2 | 7 |
| 7,5 | 8 | 8,3 | 7,2 |
| 9,1 | 9,2 | 10,9 | 9 |
| 6,8 | 10,4 | 9,4 | 8,1 |
| 10,1 | 7,1 | 8,5 | 6,1 |
| Т=8,16 | m=0,12255 | ||
Рассматриваем два типа шин: питающие шины, идущие от трансформатора к вводному выключателю; секции шины. Так как шины голые то для них применим показательный закон распределения внезапных отказов. Причиной внезапных отказов является воздействие токов короткого замыкания. Расчет произведем аналогично результаты расчетев сведем в таблицу 20,21,22,23
Таблица 20
Статистический ряд внезапных отказов питающих шин
| X, ч | X, ч | X, ч | X, ч |
| 760215 | 856936 | 768768 | 867865 |
| 1001326 | 870594 | 1001022 | 874998 |
| 794916 | 905950 | 964405 | 814378 |
| 969966 | 956631 | 840253 | 903270 |
| 888089 | 806707 | 894381 | 823804 |
| Т= | 878224 | l= | 1,14E-06 |
Таблица 21
Статистический ряд времени восстановления питающих шин
| восстановление | |||
| 2,1 | 2,9 | 2,3 | 3,5 |
| 3,7 | 3,8 | 3,8 | 3,9 |
| 3,0 | 4,3 | 3,0 | 3,7 |
| 4,4 | 3,9 | 4,7 | 2,4 |
| 3,3 | 3,6 | 3,1 | 4,2 |
| Т=3,48353 | m=0,28707 | ||
Таблица 22
Статистический ряд внезапных отказов секций шин
| X, ч | X, ч | X, ч | X, ч |
| 760215 | 856936 | 768768 | 867865 |
| 1001326 | 870594 | 1001022 | 874998 |
| 794916 | 905950 | 964405 | 814378 |
| 969966 | 956631 | 840253 | 903270 |
| 888089 | 806707 | 894381 | 823804 |
| Т= | 878224 | l= | 1,1E-06 |
Таблица 23
Статистический ряд времени восстановления секций шин
| восстановление | |||
| 2,0 | 2,7 | 2,2 | 3,3 |
| 3,5 | 3,6 | 3,6 | 3,7 |
| 2,8 | 4,2 | 2,8 | 3,5 |
| 4,3 | 3,7 | 4,5 | 2,3 |
| 3,1 | 3,4 | 2,9 | 4,1 |
| Т=3,33011 | m=0,30029 | ||
Похожие работы
... (от передвижения источников загрязнения) 1180,48 Всего за год: 211845,25 10. Совершенствование системы электроснабжения подземных потребителей шахты Расчет схемы электроснабжения ЦПП до участка и выбор фазокомпенсирующих устройств Основными задачами эксплуатации современных систем электроснабжения горных предприятий являются правильное определение электриче ...
... результатов с реально существующей подстанцией, рассмотрение существующей системы релейной защиты и автоматики и определение ее эффективности. 1. ПРОВЕРОЧНЫЙ РАСЧЕТ ОБЪЕКТА ЭЛЕКТРОСНАБЖЕНИЯ 1.1. Влияние окружающей среды на работу подстанции «Правобережная» В данном проекте в качестве объекта электроснабжения рассматриваем подстанцию «Правобережная». Она работает в системе совместно с ...
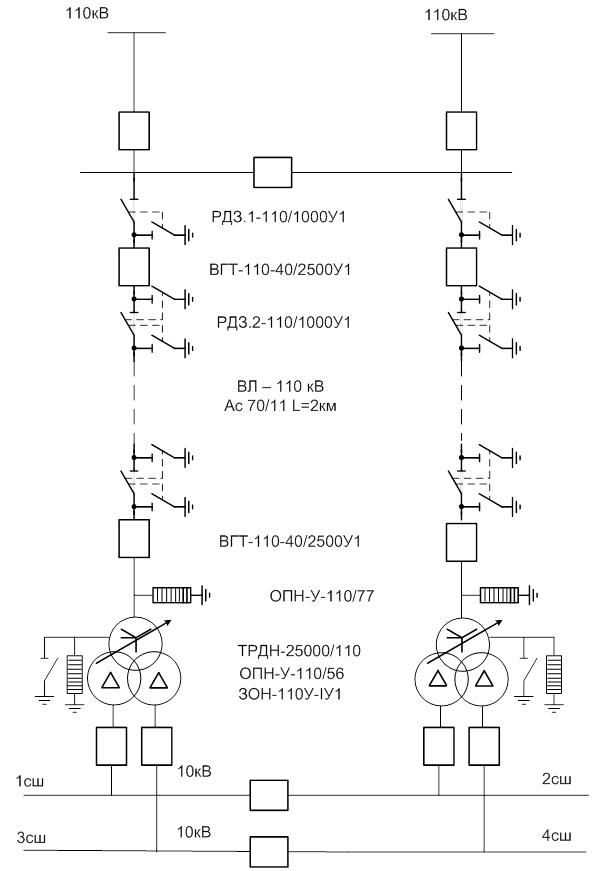
... = 0,7 для ВЛ – 110 кВ коэффициент перехода импульсной искры в силовую. При 50 грозовых часах в году (ПУЭ, Тюменская область) удельное число отключений: nоткл = h·hc·Рпер· (3.48) nоткл = 2·10·0,85·0,7 Следовательно, ВЛ-110 кВ будет работать ненадежно. Принимаем к установке грозозащитный трос. Особое внимание должно уделяться грозозащиты подстанции ( ...
... 8729;Ucp∙Ino, MBA Iпо Iпt iу К-1 115 25,1 25,1 61,06 5000 К-2 115 19,1 19,1 45,91 3803,57 К-3 10,5 8,79 8,79 20 159,92 К-4 0,4 25,92 25,92 56084 17,95 6. Выбор электрооборудования системы электроснабжения предприятия 6.1 Выбор трансформаторов собственных нужд главной понизительной подстанции Приемниками собственных нужд подстанции являются ...




0 комментариев