СИММЕТРИЯ В ГЕОЛОГИИ

4. СИММЕТРИЯ В ГЕОЛОГИИ

4.1. ЛЕГЕНДЫ РУДОКОПОВ

В старину рудокопы были людьми сугубо практическими. Они не забивали себе голову названиями всевозможных горных пород, которые встречали в штольне, а просто делили эти породы и минералы на полезные и бесполезные, ненужные. Нужные они извлекали из недр, из них плавили медь, свинец, серебро и другие металлы, а ненужные сваливали в отвалы.

Для полезных (на их взгляд) минералов они подыскивали наглядные и запоминающиеся имена. Можно никогда не видеть копьевидного колчедана, но без особого труда представить его себе по названию. Не сложнее по названию отличить красный железняк от бурого железняка.

Для бесполезных камней (как уже было сказано — на их взгляд) горняки нередко находили названия в преданиях и легендах. Так, например, произошло название руды кобальтовый блеск. Кобальтовые руды похожи на серебряные и при добыче иногда принимались за них. Когда из такой руды не удавалось выплавить серебро, считалось, что она заколдована горными духами — кобольдами.

Когда же минералогия превратилась в науку, было открыто великое множество пород и минералов. И при этом все чаще возникали трудности с изобретением для них наименований. Новые минералы часто называли по месту находки (ильменит — в Ильменских горах) или в честь знаменитого человека (гетит — в честь Гете) или же давали ему греческое или латинское название.

Музеи пополнялись грандиозными коллекциями камней, которые становились уже необозримыми. Не слишком помогали и химические анализы, потому что многие вещества одного и того же состава образуют подчас кристаллы совершенно различного облика. Достаточно вспомнить хотя бы снежинки.

В 1850 г. французский физик Опост Браве (1811—1863) выдвинул геометрический принцип классификации кристаллов, основанный на их внутреннем строении. По мнению Браве, мельчайший, бесконечно повторяющийся мотив узора и есть определяющий, решающий признак для классификации кристаллических веществ. Браве представлял себе в основе кристаллического вещества крошечную элементарную частицу кристалла. Сегодня со школьной скамьи мы знаем, что мир состоит из мельчайших частиц — атомов и молекул. Но Браве оперировал в своих представлениях крошечным «кирпичиком» кристалла и исследовал, каковы могли быть у него углы между ребрами и в каких соотношениях его стороны могли находиться между собой.

В кубе три ребра расположены всегда под углом 90° друг к Другу. Все стороны имеют равную длину. У кирпича углы тоже составляют 90°. Но его стороны различной длины. У снежинок, наоборот, мы не найдем угла 90°, а только 60 или 120°.

Браве установил, что существуют 7 комбинаций ячеек с одинаковыми или разными сторонами (осями) и углами. Для углов он принял только два варианта: равный 90° и не равный 90°. Только один угол во всей его системе в порядке исключения имеет 120°. В самом скверном случае все три оси и все углы ячейки различны по величине, при этом в ней нет углов ни в 90, ни в 120°. Все в ней косо и криво, и, можно подумать, в мире кристаллов таким не должно быть места. Между тем к ним относится, например, сульфат меди (медный купорос), голубые кристаллы которого обычно всем так нравятся.

В некоторых из этих 7 пространственных решеток элементарные «кирпичики» можно упаковать по-разному. Для нас, знающих сегодня о строении атома, это нетрудно представить и продемонстрировать с помощью шариков для пинг-понга. Но 125 лет назад гениальная идея Браве была новаторской и открывала новые пути в науке. Весьма вероятно, что и Браве исходил из узоров кафеля или мотивов шахматной доски.

Если мы разделим квадратные поля диагоналями, то возникает новый рисунок из квадратов, стоящих на углах. В трехмерном пространстве это соответствует кубу, разложенному на шесть пирамид. Каждая такая пирамида составляет половину октаэдра.

Те, кто когда-нибудь выращивал кристаллы поваренной соли, знают, что соль может кристаллизоваться в кубах, а может — в октаэдрах. Иными словами, экспериментальные наблюдения совпадают с теоретическими соображениями.

Испробовав возможные варианты упаковки для всех семи осевых систем, Браве вывел 14 решеток.

Рассматривая решетки Браве внимательней и пробуя мысленно построить из них кристаллы, мы, вероятно, увидим, как можно провести в них плоскости и оси симметрии. Эти возможности сразу расширятся, если мы в одной из элементарных ячеек образуем новые грани. Возьмем куб, поставим его на угол и обрежем (все так же мысленно) все углы, тогда у него образуются совершенно новые треугольные грани. А из квадратных граней возникнут восьмиугольники: тем самым появятся новые мотивы симметрии.

Анализ элементов симметрии в каждой из осевых систем кристаллических решеток приводит к возникновению 32 классов симметрии. Все многообразие минералов в природе подразделяется на основе 32 классов симметрии. Вооруженные этими знаниями, задумаемся о классификации пяти тел Платона. То, что куб, с его тремя равными осями и тремя прямыми углами, относится к кубической осевой системе (сингонии), не нуждается в доказательстве. В рамках более детального подразделения он принадлежит пентагон - тетраэдрическому классу симметрии. Не стану здесь приводить названий других классов из-за их сложности. Однако стоит обратить внимание на термин «тетраэдрический», так как тетраэдр — одно из платоновых тел.

Тетраэдр можно образовать из куба. Остальные платоновы тела также относятся к кубической системе. Древние греки, надо думать, ужасно расстроились бы, знай они, что такой прозаический минерал, как серный колчедан, имеет ту же симметрию, что и их «совершенные» тела.

4.2.СИММЕТРИЯ ПОМОГАЕТ ОТКРЫВАТЬ МЕСТОРОЖДЕНИЯ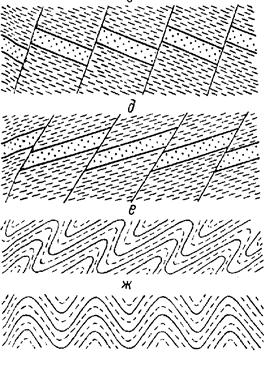

Можно обнаружить широкое распространение проявлений симметрии в строении геологических тел самых различных размеров и происхождения, входящих в состав земной коры. Среди этих проявлений симметрии значительную часть составляют разнообразные симметричные структуры, образование которых связано с разрядкой механических напряжений, возникающих в геологических телах по разным причинам (тектонические движения, сокращение объема при охлаждении или дегидратации и т. д.). Обращение к симметрии этих структур, к закономерной повторяемости их элементов (структурных форм) позволяет подойти к рассмотрению механизмов образования таких структур с принципиально новых позиций.

До сих пор говорилось лишь об элементах симметрии и их сочетаниях, т. е. об общих закономерностях повторяемости фигур и их частей. В кристаллографии, как известно, этим дело не ограничивается, а, исходя из тех же законов симметрии, выводятся формы кристаллических фигур.

Рис. 1. Примеры симметричного распределения геологических структурных форм. б — "лестничные" жилы; д — ступенчатый сброс; е — наклонные складки; ж — прямые складки.

Вспомним, что простыми гранными формами называются совокупности граней, связанных друг с другом элементами симметрии. По-видимому, в некоторых случаях целесообразно воспользоваться этими понятиями геометрической кристаллографии и применить их для характеристики геологических объектов.

В качестве примера рассмотрим простейшие формы блоков пород, изображенные на рис. 2. Так, например, купола, конусовидные вулканы, кольцевые дайки, штоки и некоторые другие структуры обладают вертикальной осью симметрии бесконечного (полная их симметрия — симметрия конуса L P — т). Из других осей симметрии в геология чаще всего встречаются оси второго порядка. Например, симметрия сундучных складок L2 2P — 2mm (рис. 2).

Вспомнив кристаллографические модели простых форм и их комбинаций, мы без труда найдем здесь пинакоиды, различные призмы и кубы. Конусообразную форму вулкана можно уподобить п-гональной пирамиде, а горные хребты — комбинациям диэдров.

Рис. 2. Простые геологические структуры: а) куполообразная; б) сундучная.

Нам могут возразить, что приведенные здесь и далее примеры являются сугубо идеализированными. Однако вспомним, что и кристаллографические модели являются обобщенными идеализациями реальных форм. Идеализация с помощью статистических данных широко используется кристаллографами. Очевидно, аналогичные приемы могут быть рекомендованы и для геометризации геологических объектов.

Возникает вопрос: почему геометрические закономерности в распределении структурных форм сравнительно редко отмечались до сих пор в геологической литературе.

По-видимому, имеется ряд причин, затрудняющих их выявление. Выше уже говорилось о необходимости обобщать и статистически идеализировать такие явления. Неоднородность строения геологических тел и их масштабы затрудняют подобные исследования. Следует иметь в виду также и то, что зачастую мы имеем дело со случайными срезами, неблагоприятными для выявления закономерностей симметрии. Кроме того, сами закономерности симметрии могут быть. достаточно сложными (например, в случае наличия плоскостей скользящего отражения или винтовых осей) и не бросаются в глаза при случайном взгляде на случайный срез структуры. Наконец, играют роль и некоторая сложность понятийного аппарата симметрии и недостаточная устремленность геологов пользоваться им.

Вместе с тем еще и еще раз следует подчеркнуть, что симметрия геологических образований подчиняется в общем тем же законам симметрии, которые хорошо известны в геометрии и кристаллографии. Анализ сетчатых систем трещин с особой убедительностью иллюстрирует сказанное. Во всех разобранных выше примерах не встречалось ни одного элемента симметрии и ни одной их совокупности, которые не были бы известны кристаллографам (оси бесконечного порядка, невозможные для кристаллических полиэдров, широко используются при характеристике оптических индикатрис). Пространственные группы Е. С. Федорова, сетки и решетки О. Браве, симметрия лент, бордюров и стержней — все это широко реализуется в геологических структурах.

Подводя некоторый итог, следует особо подчеркнуть всеобъемлющее значение строго математических законов симметрии пронизывающих все естествознание, а тем самым охватывающих и все без исключения объекты геолого-минералогических наук.

Исключительную роль в этом отношении играет вытекающий из принципа П. Кюри закон формирования природных тел в поле земного тяготения:

«Все что растет или движется по вертикали приобретает симметрию Ln nP — пт, все, что растет или движется по горизонтали, получает симметрию Р — т (или — —1)».

Невольно напрашивается идея о широком использовании этого закона для выявления процессов формирования геологических объектов.

При рассмотрении разнородных геологических образований нам пришлось помимо классической использовать новые понятия расширенной симметрии, учения об антисимметрии и динамической симметрии. Все эти понятия образуют единый методологический комплекс. Учение о симметрии в геологи, формирующееся на границе геометрической кристаллографии и наук геологического цикла, является сейчас новым научным направлением, требующим всемерного углубления и дальнейшего развития. Объектом этой новой дисциплины являются геометрические закономерности как всей планеты в целом, так и отдельных ее составляющих на различных уровнях организации вещества.

Кроме отмеченного выше существенного теоретического значения широкое распространение проявлений симметрии в геологических структурах имеет важное практическое значение. Понимание законов симметрии, проявляющихся в той или иной конкретной геологической структуре, может оказать весьма существенную помощь в деятельности геологов по поискам месторождений полезных ископаемых и отдельных рудных тел в пределах известных рудных полей.

Реальные примеры проявления в геологических структурах (в том числе и в структурах рудных полей) симметрии таких типов достаточно многочисленны и многократно описаны в геологической литературе.

Разумеется, используя представление о симметрии размещения рудных тел и месторождений, при поисках необходимо учитывать существование различных факторов, ограничивающих или затрудняющих применение этих представлений. Прежде всего необходимо помнить, что в частных случаях число рудных тел в симметричной серии может быть любым. Поэтому наличие одного или нескольких рудных тел не гарантирует наличия других рудных тел, связанных с известными телами законами симметрии. Далее, следует иметь в. виду, что достаточно строгие проявления симметрии в размещении структурных форм и рудных тел возможны лишь в достаточно однородной (в том масштабе, в котором ведется исследование) среде. Различного рода неоднородности среды, в которой размещены рудные тела, могут обусловливать в различной степени существенные отклонения от строгой симметрии.

Однако практически достаточно знать глубины выклинивания известных рудных тел, чтобы определить места возможного нахождения «слепых» рудных тел, принадлежащих этим симметричным сериям. Очевидно, что поиск рудных тел таким методом будет в этих случаях во много раз эффективнее, чем поиск путем разбуривания рудного поля по сетке, не увязанной с симметрией его структура.

Учтя такую возможность, мы сможем в этом случае выявить все рудные тела с минимальной затратой сил и средств.

Выявление симметрии размещения и внутреннего строения тектонических структур и других геологических образований, контролирующих размещение полезных ископаемых, помимо теоретического интереса, имеет и огромное прикладное значение и поэтому должно считаться одной из первоочередных задач геологической науки на современном этапе ее развития.